Точки покоя.

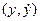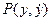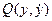Определение 24.2. Точка фазовой плоскости системы (24.6) называется обыкновенной точкой, если и дифференцируемы и не обращаются одновременно в нуль; через каждую обыкновенную точку проходит одна фазовая траектория. Точка 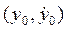называется особой точкой, есл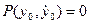и и .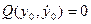

Замечание. Особые точки классифицируются по характеру фазовых траекторий в их окрестности.

Исследование на устойчивость некоторого решения 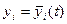системы (24.1) можно свести к исследованию тривиального решения – точки покоя, расположенной в начале координат, преобразуя систему к новым переменным: 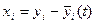- отклонениям прежних неизвестных от решения, исследуемого на устойчивость. В новых переменных система (24.1) принимает вид:

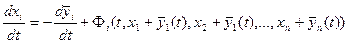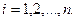, (24.8)

Простейшие типы точек покоя.

Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:

, где 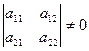. (24.9)

Характеристическое уравнение при этом имеет вид:

.

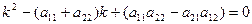Рассмотрим различные наборы корней этого уравнения:

1) k₁ и k₂ действительны и различны. Тогда общее решение системы (24.9) можно задать так: 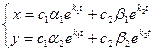. При этом возможны следующие случаи:

а) если k₁ < 0 и k₂ < 0, то точка покоя асимптотически устойчива, так как 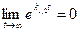, и все точки, находящиеся в начальный момент t = t₀ в любой δ – окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой ε – окрестности начала координат, а при 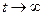стремятся к началу координат. Такая точка покоя называется устойчивым узлом.

б) если k₁ > 0, k₂ >0, можно свести исследование к предыдущему случаю заменой t на –t. При этом фазовые траектории имеют такой же вид, но направление движения меняется на противоположное, то есть при увеличении t точка удаляется от начала координат, поэтому подобная точка покоя – неустойчивый узел – неустойчива по Ляпунову.

в) при k₁ > 0, k₂ < 0 точка покоя тоже неустойчива, так как движущаяся по траектории

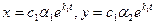точка с возрастанием t выходит из ε – окрестности начала координат. Точка покоя рассматриваемого типа называется седлом.

2) k_1,2 = p ± qi . Тогда общее решение системы (24.9) можно представить в виде

, где 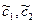- линейные комбинации произвольных постоянных с₁, с₂. При этом возможны следующие случаи:

а) p < 0, q ≠ 0. Тогда при 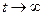, а тригонометрические функции являются ограниченными. Поэтому фазовые траектории являются спиралями, асимптотически приближающимися при 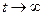к началу координат. Таким образом, точка покоя асимптотически устойчива. Она называется устойчивым фокусом.

б) p > 0, q ≠ 0. Изменяется направление движения по фазовым траекториям, следовательно, точки удаляются от начала координат и точка покоя неустойчива – неустойчивый фокус.

в) р = 0. Траекториями являются замкнутые кривые, окружающие точку покоя, называемую в этом случае центром. Такая точка покоя устойчива, так как можно подобрать такое δ, что замкнутые траектории, начальные точки которых лежат в δ – окрестности начала координат, не выходят за пределы ε – окрестности начала координат (x² (t) + y² (t) < ε² ).

3) Корни кратны: k₁ = k₂.

а) k₁ = k₂ < 0. Тогда общее решение 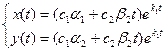стремится к нулю при 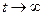, и точка покоя вновь называется устойчивым узлом. При 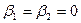получаем частный случай устойчивого узла – так называемый дикритический узел.

б) k₁ = k₂ > 0. Направление движения по траекториям меняется - неустойчивый узел.