Задача Коши для трехмерного волнового уравнения.
Называется задача нахождения функции 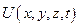 , удовлетворяющая уравнению
, удовлетворяющая уравнению
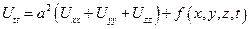
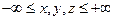
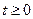

 , где
, где
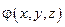 – начальное распределенное электромагнитное поле в заданной среде
– начальное распределенное электромагнитное поле в заданной среде
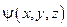 – начальная скорость изменения электромагнитного поля в заданной среде.
– начальная скорость изменения электромагнитного поля в заданной среде.
Решение этой задачи существует и единственно и выражается формулой Кирхгофа:
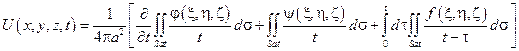 ,
,
где:
Sat – сфера радиуса at с центром в точке (x,y,z),
Sa(t-τ) – сфера радиуса a(t-τ)с центром в точке (x,y,z).
Пример:
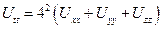
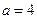
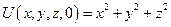
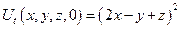
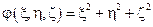
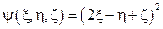
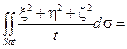
| 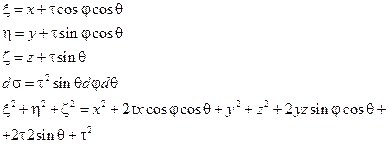
|
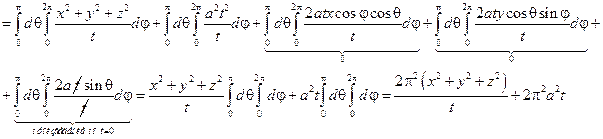
Решение не правильное
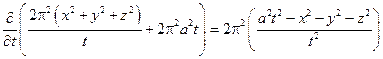
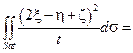
| 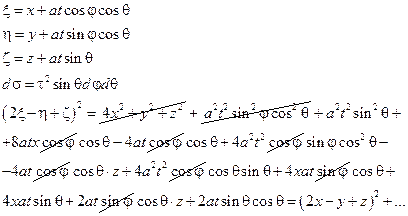 все слагаемые, которые содержат sin φ и cos φ интеграл будут равны нулю.
все слагаемые, которые содержат sin φ и cos φ интеграл будут равны нулю.
|
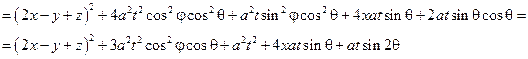

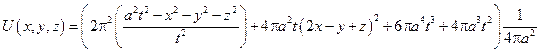
Пример:
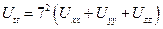
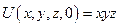
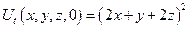

| 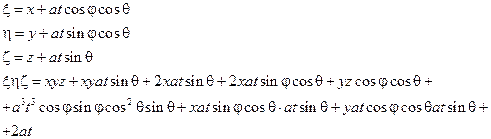
|
Решение краевых задач для одномерного волнового уравнения методом разделения переменных (Фурье)
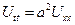
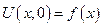
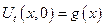
Эта задача интерпретировать малые поперечные колебания струны без воздействия внешних сил (свободные колебания), струна имеет конечную длину 0 ≤ x ≤ l, в каждой точке этой струны задано начальное ее отклонение равновесного положения и начальная скорость. Будем пока считать, что концы струны жестко закреплены, что соответствует краевому условию
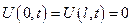
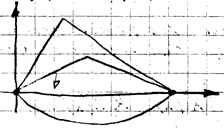
Будем искать решение поставленной задачи
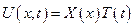 , тогда
, тогда
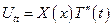 и
и 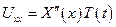
поставим эти уравнения в начальное уравнение.
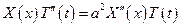
для того, чтобы проинтегрировать раздел. переменные
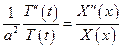
поскольку последнее равенство выполнено для любых значений Х и Т, то найдется такое число К, что
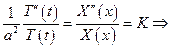
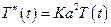
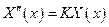
из краевых условий 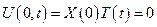 =>
=> 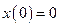
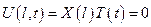 =>
=> 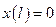
Следовательно, для нахождения функций Х(х) и Т(t) получаем две задачи
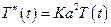
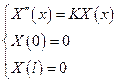
1-ый случай: К > 0, тогда
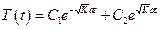
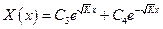 , где С1, С2, С3, С4 – произвольные постоянные.
, где С1, С2, С3, С4 – произвольные постоянные.
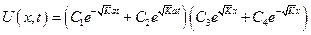
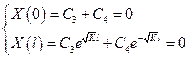
Система однородная, определитель ≠ 0.
Полученная система на С3 и С4 будет иметь отличное от нуля решение только в том случае, если определитель = 0.
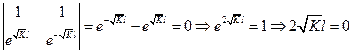 К = 0, что противоречит, что К = 0.
К = 0, что противоречит, что К = 0.
2-ой случай: К = 0
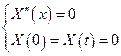 =>
=> 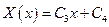
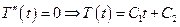
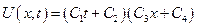
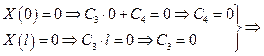
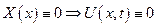
3-ий случай: К < 0
Положим 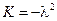
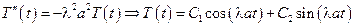
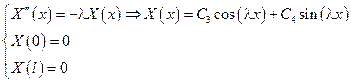
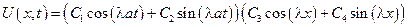
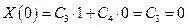
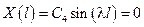
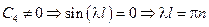
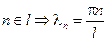
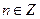 – собственные значения поставленной задачи штурма – Муввиля, каждая из которых:
– собственные значения поставленной задачи штурма – Муввиля, каждая из которых:
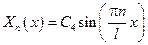
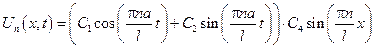

Пользуясь принципом суперпозиции решения однородных задач, получаем, что общее решение будет иметь вид:
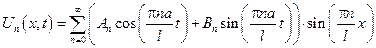
Для определенных коэффициентов An и Bn воспользуемся начальными условиями
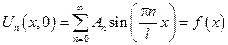 – ряд Фурье.
– ряд Фурье.
Функция f(x) по синусам, а An – коэффициент ряда Фурье по функциям f(x).
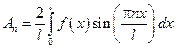
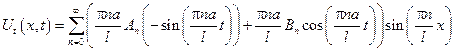
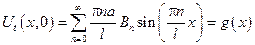 – это разложение функции g(x) в ряд Фурье.
– это разложение функции g(x) в ряд Фурье.
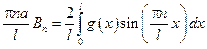
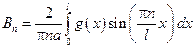
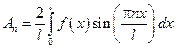
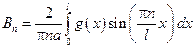
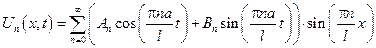
Пример: Тугонатянутая гибкая струна. Книга Троицкой, стр. 23, задача 4
«Смешанная задача для волнового уравнения в прямоугольнике»
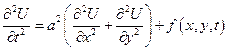
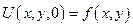
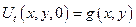
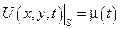 , где S – граница области, в которой ищется решение.
, где S – граница области, в которой ищется решение.
Пусть теперь мембрана имеет вид прямоугольника.
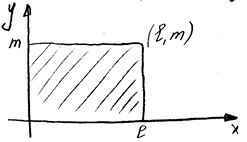
воздействие внешних сил не учитываем
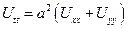
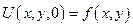
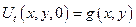
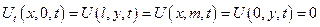
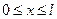
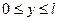
Применим метод разделения переменных
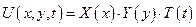
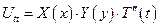
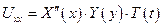
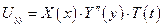
Подставим эти выражения для производных в исходное уравнение:
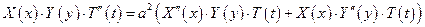
разделим это равенство на
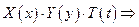 получим:
получим:
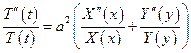
Причем последнее равенство выполнено для любых точек x, y, t => существует постоянное число λ, такое что
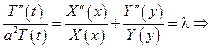

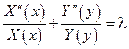
Причем, последнее равенство выполнено при любых x и y => найдутся числа λ1 и λ2 такие что:
λ = λ1 + λ2 и
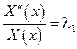 , а
, а 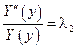
Из граничных условий:
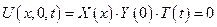 для любых точек x и t =>
для любых точек x и t =>
Y(0) = 0
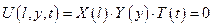 для любых точек y и t =>
для любых точек y и t =>
X(l) = 0
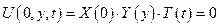 для любой точки y, t =>
для любой точки y, t =>
X(0) = 0
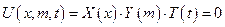 для любой точки x, t =>
для любой точки x, t =>
Y(m) = 0
Следовательно, получаем две задачи Штурма – Люнвина для нахождения функций X(x) и Y(y).
Задачи:
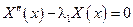
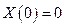
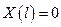 1. Пусть λ1 > 0, тогда
1. Пусть λ1 > 0, тогда
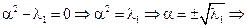
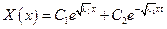
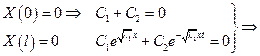 C1 = C2, т.к.
C1 = C2, т.к. 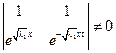 λ1 > 0 быть не может
λ1 > 0 быть не может
| 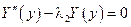
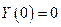
 1. Аналогично левому столбику, можно показать, что λ2 > 0 быть не может
1. Аналогично левому столбику, можно показать, что λ2 > 0 быть не может
|
2. λ1 = 0 X(x) = ax + b
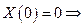 b = 0 b = 0
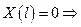 a = 0
λ1 ≠ 0
решение тривиальное a = 0
λ1 ≠ 0
решение тривиальное
| 2. Аналогично λ2 ≠ 0 |
3. λ1 < 0
Характеристическое уравнение
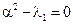
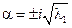
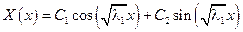
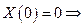 С1 = 0 С1 = 0
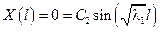
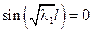
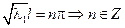
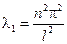 – бесконечно много собственных значений задачи Штурмана – Люнвина – бесконечно много собственных значений задачи Штурмана – Люнвина
| λ2 < 0
Характеристическое уравнение
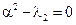
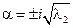
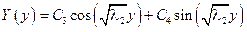
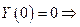 С3 = 0 С3 = 0
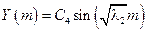
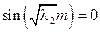
 
 – бесконечно много собственных значений – бесконечно много собственных значений
|
Каждое из найденных собственных значений порождает собственную функцию
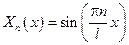
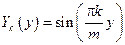
Следовательно:
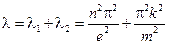
Найдем T(t)
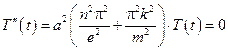
Характеристическое уравнение:
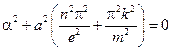
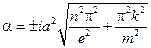
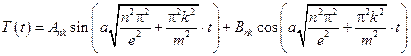
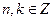 – бесконечное число собственных функций задачи Штурмана – Люнвина, на нахождение функции T(t), тогда общее решение исходной задачи будем искать в виде:
– бесконечное число собственных функций задачи Штурмана – Люнвина, на нахождение функции T(t), тогда общее решение исходной задачи будем искать в виде:
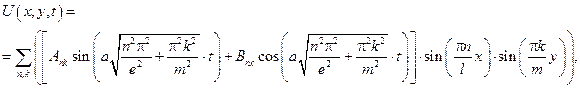
где Ank и Bnk – определяются, исходя из начальных условий
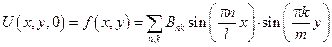
Не трудно показать, что система функций
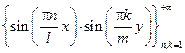 – ортогональная система функций на прямоуг
– ортогональная система функций на прямоуг
Bnk – коэффициент Фурье, разложения функции f(x,y) в ряд Фурье по этой системе =>
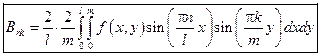
Воспользуемся заданной начальной скоростью для нахождения коэффициента Ank.
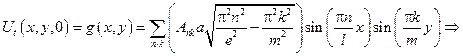
откуда получаем, аналогично предыдущему, что
 – коэффициент Фурье разложения функции g(x,y) в ряд Фурье по системе функций
– коэффициент Фурье разложения функции g(x,y) в ряд Фурье по системе функций
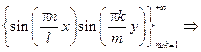
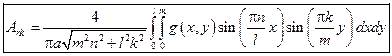
22 вариант (14)
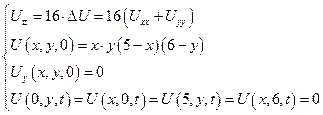

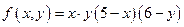
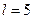
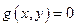
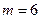
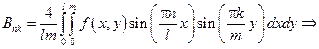
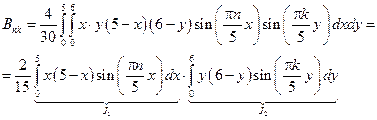
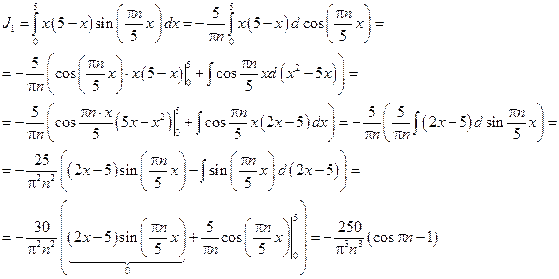
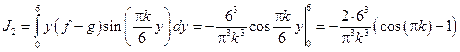
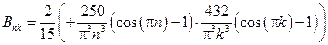
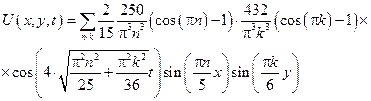
|
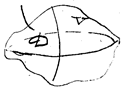
U(t,x,y,z) – температура в точке 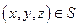 в момент времени t.
в момент времени t.
Воспользуемся законом Фурье для плотности потока тепла W в направлении нормали 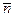 в единицу времени.
в единицу времени.
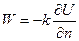 , где
, где 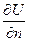 – производная функции температуры U(t,x,y,z) вдоль нормали
– производная функции температуры U(t,x,y,z) вдоль нормали 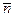 , k – коэффициент теплообмена.
, k – коэффициент теплообмена.
k – может быть функцией температуры, точки, времени, т.е. 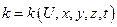 .
.
Рассмотрим часть тела V ограниченную поверхностью S.
Напишем уравнение баланса тепла в объеме D за малое время Δt.
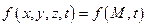 – где М – точка объема D – функция плотности тепла от внешних источников, тогда Q1 – количество тепла от внешних источников.
– где М – точка объема D – функция плотности тепла от внешних источников, тогда Q1 – количество тепла от внешних источников.
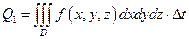 – количество тепла, пришедшее в объем D за счет внешних источников за время Δt.
– количество тепла, пришедшее в объем D за счет внешних источников за время Δt.
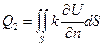 – расход тепла за счет выходящего из D потока.
– расход тепла за счет выходящего из D потока.
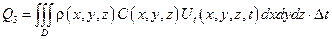 – изменение количества тепла в области D за время Δt, где
– изменение количества тепла в области D за время Δt, где
С(x,y,z) – теплоемкость тела (вещества) в точке x,y,z;
ρ(x,y,z) – плотность вещества;
Ut(x,y,z,t) – изменение температуры.
Уравнение баланса тепла по закону сохранения энергии имеет вид:
Q3 = Q1 – Q2
или в интегральной форме
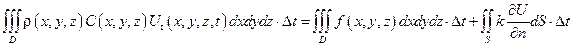
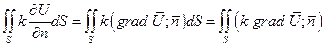 (*)
(*)
U(x,y,z) 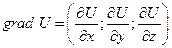
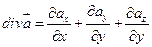
где 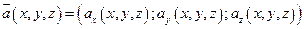
Поток векторного поля через поверхность S:
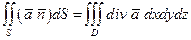 – теорема Остроградского – Гаусса.
– теорема Остроградского – Гаусса.
Применим теорему Остроградского – Гаусса к последнему интегралу (*).
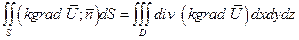 ,
,
тогда уравнение теплового баланса приобретает вид:
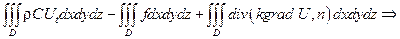

Последнее равенство выполнено для любой области D, целиком лежащей в объеме V; в виду произвольности области D, получаем уравнение теплопроводности:
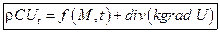 уравнение теплопроводности, уравнение распространения тепла в объеме V.
уравнение теплопроводности, уравнение распространения тепла в объеме V.
ρ, C, k – функции от М(x,y,z) и времени t;
k – коэффициент теплообмена (Фурье).
Интересный случай, когда среда однородная, т.е. ρ, C, k – постоянные и не зависят ни от положения точки, ни от времени, тело – однородно и его характеристики с течением времени не меняются, тогда
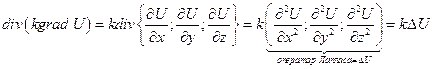
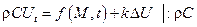
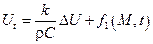 , обозначим
, обозначим 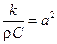 – получим =>
– получим =>
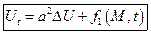 уравнение теплопроводности для однородного тела.
уравнение теплопроводности для однородного тела.
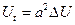 – однородное уравнение теплопроводности.
– однородное уравнение теплопроводности.
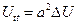 – волновое уравнение.
– волновое уравнение.
Уравнения теплопроводности принадлежат к классу уравнений параболического типа.
Доказательство:
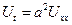
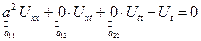
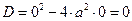
Совершенно аналогично выводится уравнение диффузии.
Воспользуемся законом Нернста для потока вещества W в направлении 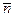 .
.
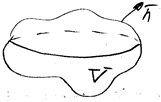
U(M,t) – концентрация диффундированного вещества в точке М объема V в момент времени t.
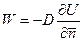 , где
, где
D – коэффициент диффузии.

f(M,t) – количество вещества, попадающего в точку М от внешних источников.
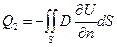 - диффунд. из тела, выходящий поток в-ва
- диффунд. из тела, выходящий поток в-ва
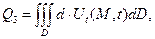 где
где
d – коэффициент пористости среды, в котором происходит диффузия
Аналогично пред. можно показать, что из уравнения:
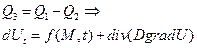
Уравнение диффузии, отлич. от уравнения теплопроводн. только тем, что коэффициенты D и d имеют другой физический смысл, если считать, что среда однородная, то уравнение приобретет вид
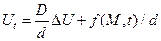 , обозначим
, обозначим 
Функция конечного вещества
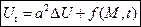
Уравнение диффуз и распространенного тепла в некотором объеме одинаковы.
В 1-ом случае:
U(M,t) – конц. вещества в V
2-ом U(M,t) - темпер.
Уравнение теплопроводн. имеет множество решений, чтобы было единственным нужно задать начальные и краевые условия
Начальные и краевые условия для уравнения теплопроводности
Ut=a2(Uxx+Uyy+Uzz)+f(x,y,z,t)
Начальные условия:
U(x,y,z,0) = f(x,y,z) – нач. температ. (нач. концентр. некот. в-ва, заданные в каждой точке некоторого объема V.
Краевые условия: 1-ого типа
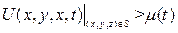 - температура, поддерживаемая на границе объема V и меняющаяся с течением времени по закону
- температура, поддерживаемая на границе объема V и меняющаяся с течением времени по закону 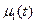
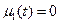 - подерж. температ. 0
- подерж. температ. 0
2 тип:
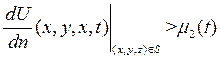 - на границе объема V задан некий закон, по которому происходит теплообмен с течением времени
- на границе объема V задан некий закон, по которому происходит теплообмен с течением времени
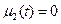 - теплообмена нет (поверхность теплоизолирована)
- теплообмена нет (поверхность теплоизолирована)
(вещество не диффунд., через поверхность объема V)
3 тип:
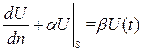
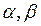 - некотор. числа
- некотор. числа
Одновремен. учитыв и изменен потока и температура на краю (границе)
1-ый и 2-ой тип – частные случаи 3-его типа
1. Боковая поверхность стержня 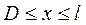 теплоизолирована
теплоизолирована
Начальная температура = φ(x)
U(x,t) – температура в стержне при t >0, для случаев когда концы стержня теплоизолированы.

2. В трубке длины l сечения S однор. пористая,  - начальная концентрация.
- начальная концентрация.
t >0 – боковая поверхность трубки не проницаемая на конце x=l с момента t=0, поддерж. конц. газа 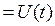 ;
;
х=0 – газонепроницаем.
U(x,t) – конц. диффуз. вещества в т. Х в момент времени t

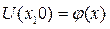
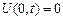
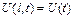

Задачи Коми для уравнения теплопроодности
Рассмотрим однородные уравнения теплопроводности.
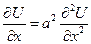
При отсутствии внешних источников тепла. Поставим задачу Коми:
Найти функцию U(x,t) удовлетворяющую уравнению:
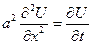
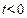
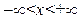
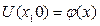
Физический смысл задачи – определение температуры однородного бесконечного стержня в любой момент времени 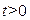 по известн. температуре
по известн. температуре  в начальный момент времени t=0.
в начальный момент времени t=0.
Считается, что токов. поверхность стержня теплоизолирована (тепло из стержня не уходит)
Предположим теперь, что функции U(x,t) и  достаточно гладкие функции, убывающие при
достаточно гладкие функции, убывающие при 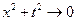
Настолько быстро, что существ. преобразов. Фурье
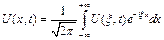 преобразование Фурье функции
преобразование Фурье функции 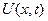 по перемен. Х.
по перемен. Х.
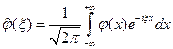
2. Законны операции дифферен.
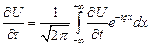 и
и
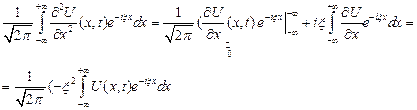
Следовательно, получаем, что преобразов. Фурье второй производной функции 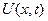 связано с преобразованием Фурье самой функции
связано с преобразованием Фурье самой функции 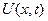 следующ. равенством
следующ. равенством
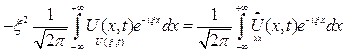
Применим преобразов. Фурье к исходному уравнению и нач. услов. сведя пост. задачу к задаче Коши для обыкновенного дифференциального уравнения

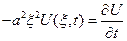
От первого уравнения осталось уравнение:
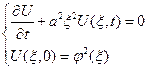 -
-
Полученная задача, является задачей Коми для обыкновенного дифференц. уравнения.
Решением этой задачи является функция
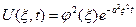 (что проверяется простой подстановкой)
(что проверяется простой подстановкой)
Покажем, что функция
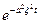 является преобразованием Фурье
является преобразованием Фурье
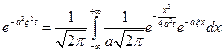
Т.е. явл. преобразов. Фурье от функции:
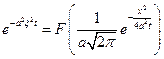
Док-во: считаем
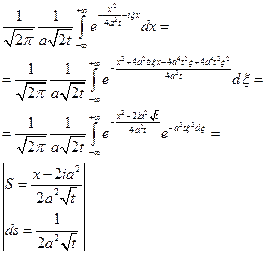
Мы доказали, что функция
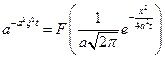
и наше решение
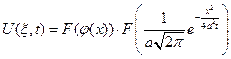
Решение  можно записать в виде:
можно записать в виде:
Как известно произведение двух преобразований Фурье = свертке преобраз. функций равна преобраз. Фурье от свертки преобразуемых функций
т.е. 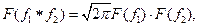 где f1 свернутая с f2
где f1 свернутая с f2
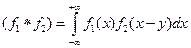
Тогда
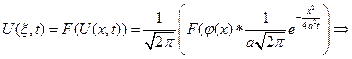
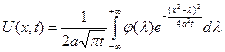
Получено решение исходной задачи Коши и назыв. формула Пуассона для решения задачи Коши уравнения теплопроводности.
Осталось проверить, что заданное уравнение удовлетворяет начальному условию, т.е. 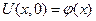
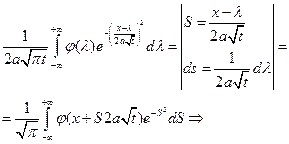
При 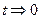 находим, что
находим, что
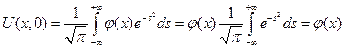 ч.т.д.
ч.т.д.
Найденное решение удовлетворяет условию:
Пример:

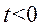
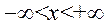
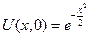
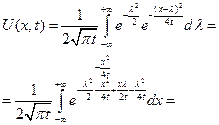
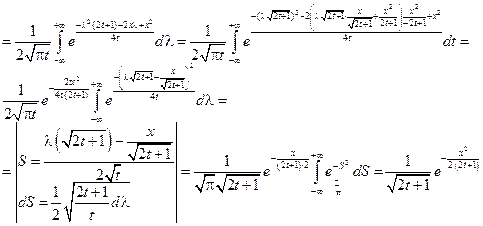 ,
,
Фундаментальное решение уравнения теплопроводности ( 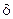 - функция Дирана)
- функция Дирана)
Функция

Входящая в формулу Пуассона назыв. фундаментал. решение уравнений теплопроводности.
Рассматривая как функция аргументов x,t она удовлетворяет уравнению теплопроводности
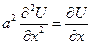 в чем можно убедится проверкой.
в чем можно убедится проверкой.
Фундаментальное решение имеет важный физический смысл, связанный с понятием теплового импульса. Допустим в начальный момент времени начальное распределение температуры имеет вид:
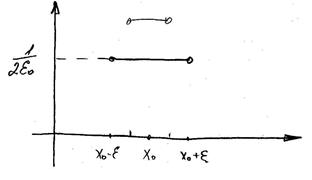
|
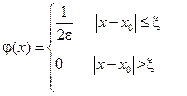
Чем меньше 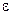 тем выше полочка
тем выше полочка
Тогда в силу формулы Пуассона распределен. температуры в стержне имеет вид:

по теореме о среднем найдется такая точка
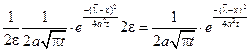 , где
, где 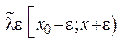 устремим
устремим 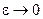 , тогда
, тогда  из последнего равенства получим
из последнего равенства получим
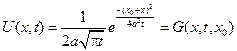 - это означает, что функция
- это означает, что функция 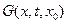 представляет распределенную температуру в стержне в момент
представляет распределенную температуру в стержне в момент 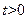 , если начальный момент времени
, если начальный момент времени 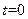 в точке х0 имеется бесконечный пик температур, а в остальных точках стержня температура равна была 0. Такое начальное распределение температур может быть приближ. реализовано следующим образом:
в точке х0 имеется бесконечный пик температур, а в остальных точках стержня температура равна была 0. Такое начальное распределение температур может быть приближ. реализовано следующим образом:
В момент 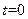 к точке х0 стержня на очень короткий промежуток времени подносится узкое пламя очень высокой температуры (тепловой импульс) – это начальное распределение температур описыв. Формулой Дирана и обозначается
к точке х0 стержня на очень короткий промежуток времени подносится узкое пламя очень высокой температуры (тепловой импульс) – это начальное распределение температур описыв. Формулой Дирана и обозначается 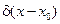 . Не явл. функцией в обычном смысле
. Не явл. функцией в обычном смысле 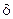 функция определена формально при помощи соотношений
функция определена формально при помощи соотношений
1. 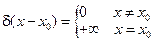
2. 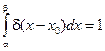 для любого интервала
для любого интервала 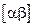 , содерж. точку х0
, содерж. точку х0
3. 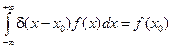
Таким образом фундамент. решение 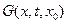 явл. решением уравнения стержня при начальном распределение температур
явл. решением уравнения стержня при начальном распределение температур
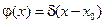
Д/з стр. 31
Дата добавления: 2015-02-28; просмотров: 5410;
