Оператор Лапласа в полярных координатах

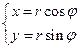
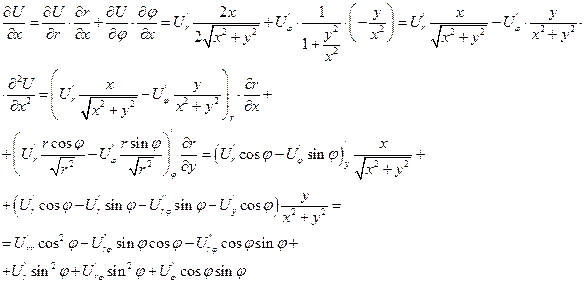
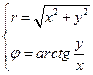
анологично:
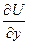 и
и 
И подставим их в оператор Лапласа и получим его в полярных координатах:
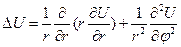
В цилиндрических координатах:
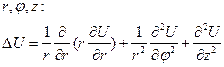
В сферических координатах
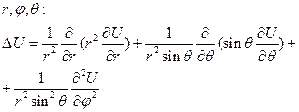
Ясно что эти представл. оператором Лапласса для упрощения решения и постановки задачи в некоторых специальных областях.
Полярные – круговые области
Цилиндрические – цилиндрические области
Сферические – сферические области
Кроме уравнений Лапласа и Пуассона к электрическим относятся еще целый класс других уравнений.
Уравнение Гельмгольца – называется уравнение вида:
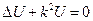 , где
, где  - заданное постоянное число.
- заданное постоянное число.
Уравнение Гельмгольца является важным видом электрических уравнений этого порядка.
Оно естественно возникает в многомерном случае в методе разделения переменных для гиперболических и параболических задач.
Нахождение собственных функций и значений сводится к разрешим. соотв. краевой задачи для уравнения Гельмгольца.
Решаем внутреннюю задачу Дирихле для уравнения Гельмгольца в круге.
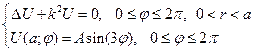
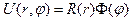
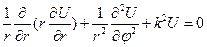
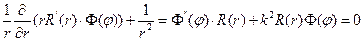

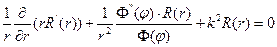
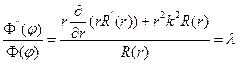
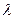 - постоянное число.
- постоянное число.
Собственные значения и функции определяются как решение уже хорошо известной нам задачи.
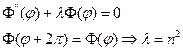 , а
, а
Решением этой задачи является соотв. собств. функции
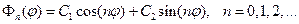
Поскольку
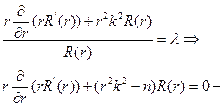
Уравнение для определения функции 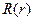
Заменим 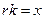 , тогда
, тогда
 - уравнение Бесселя порядка n.
- уравнение Бесселя порядка n.
Общее решение уравнения Бесселя можно записать в виде:
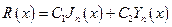 , где
, где
Jn(x) – функция Бесселя первого рода n-го порядка,
Y n(x) – функция Бесселя второго рода n-го порядка,
С1 и С2 – произвольная постоянная.
Тогда собственными функциями уравнения
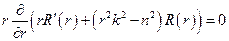
будут функции
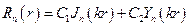 , но
, но 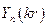 стремится к ∞, если r → 0, но нас интересуют только ограниченные решения, поэтому полагаем
стремится к ∞, если r → 0, но нас интересуют только ограниченные решения, поэтому полагаем
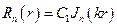 – собственная функция.
– собственная функция.
Окончательно.
Общее решение поставленной задачи можно представить в виде ряда.
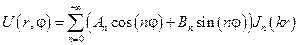
Постоянные An и Bn находим из граничного условия
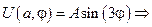
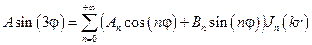
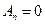 , n = 0, 1, 2, ......
, n = 0, 1, 2, ......
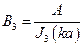 , Bn = 0 (n ≠ 3)
, Bn = 0 (n ≠ 3)
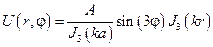
Пример. Задача №20 (вариант 15)
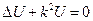
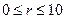
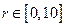
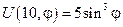
Решение:

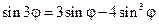
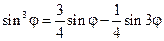
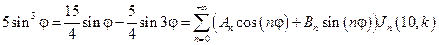
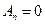
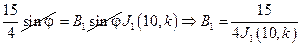

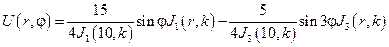
Вариант №4.
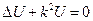
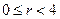
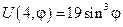
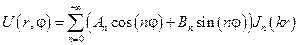
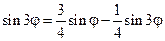
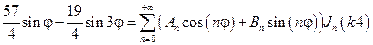
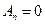
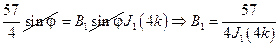
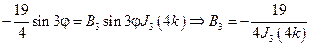
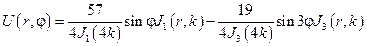
Дата добавления: 2015-02-28; просмотров: 9718;
