Уравнения эллиптического типа.

Определение. Постановка краевых задач.

Помимо физических явлений, развивающихся в пространстве и во времени, существует много явлений (распр. гравитационного и электростатического потенциала в точке свободного пространства, изменение температуры однородной изотропной среды при устан. движении тепла) которые не изменяются с течением времени.

Эти явления в большинстве случаев описаны уравнениями Лапласа и Пуассона с краевыми условиями Дирихле, Неймана и смешанного типа.

Эллиптические уравнения описывают стационарные процессы (не изменяющиеся с течением времени).

Определение. Трехмерным уравнением Лапласа называется уравнение

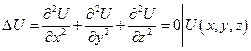
Двумерное уравнение Лапласа

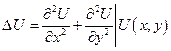
Одномерное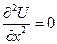

ΔU – оператор Лапласа или лапласиан.

Определение. Уравнением Пуассона называется уравнение

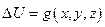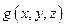, где – некоторая заданная функция.

Уравнение Лапласа описывает физический процесс без учета воздействия внешних сил, а уравнение Пуассона отвечает равновесному состоянию под действием внешней силы с плотностью, пропорциональной .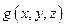

Определение. Функция 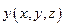называется гармонической в области , если 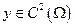и удовлетворяет в области Ω уравнению Лапласа, т.е. ΔU = 0.

В отличие от уравнения гиперб. теплов. Или теплопроводности эллиптические задачи не требуют начальных условий только краевые условия.

1. Условия краевого первого типа – Дирихле

2. Краевое условие второго типа - Неймана

3. Краевое условие третьего типа – смешанное

Краевая задача с гран. условиями первого типа (Дирихле) для уравнения Лапласа ставится так:

Требуется найти решение уравнения:

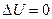в некоторой области пространства (плоскости), принимающее на границе заданное значение. В качестве примера: задача о нахождение стационарного распространения t₀ в области Ω

Пример 2: найти распределение по

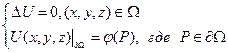и

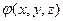известная или заданная функция

Краевая задача с гран. условиями второго типа (Неймана) для уравнения Лапласа ставится так:

Требуется найти решение уравнения 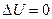в некоторой области пространства (плоскости) на границе которой задана внешняя норм. производная 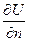пропорционально втекаемому потоку. Эта общая задача и для стац. теплопроводности и для электростатики. Если на границе задан поток (тепла 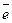) и запис. так

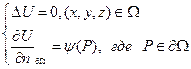
Изменение t⁰ тепла по нормали.

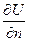- поток тепла проходящий через границу области Ω

Задача Неймана имеет смысл – только когда полный поток через границу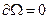

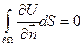
Например: задача Неймана

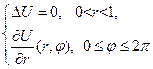
Она не имеет физического смысла, т.к. постоянный единый поток внутри области не может обеспечить стац. решения.

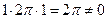
Задача не корректна.

Другой особенностью задачи Неймана для уравнения Лапласа отличающее ее от других задач является не единствен. ее решения.

Однако встречаются задачи с другими граничащими условиями – задачи гидродинамики в которых рассматриваются уравнения описываемых задач третьего типа.

Если область в которой ищется решение краевой задачи ограничено, то такая задача называется внутренней, если эта область.

То краевая задача называется внешней.

Для уравнения Пуассона задачи Дирихле и Неймана ставятся аналогично.

Вид диф. выражения в левых частях уравнений Лапласа и Пуассона одинаков во всех координатах.

При переходе к кривол. координате он изменяется.