ВРЕМЕННЫЕ УРАВНЕНИЯ СОСТОЯНИЯ И КРИТЕРИИ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ

Синтезируются жиры из глицерина и жирных кислот.

Глицерин в организме возникает при распаде жира (пищевого и собственного), а также легко образуется из углеводов.

Жирные кислоты синтезируются из ацетил-кофермента А - универсального метаболита организма. Для этого синтеза еще необходимы водород (в форме НАДФ·Н₂) и энергия АТФ. В организме синтезируются только насыщенные и мононенасыщенные (имеющие одну двойную связь) жирные кислоты. Кислоты, содержащие две и более двойных связей в своей молекуле (полиненасыщенные), в организме не синтезируются и должны поступать с пищей. Для синтеза жира также могут быть использованы жирные кислоты – продукты гидролиза пищевого и собственного жиров.

Все участники синтеза жира должны быть в активном виде: глицерин в форме глицерофосфата, а жирные кислоты в форме ацил-кофермента А. Синтез жира осуществляется в цитоплазме клеток (преимущественно, жировой ткани, печени, тонкой кищки) и протекает по следующей схеме::

Следует подчеркнуть, что глицерин и жирные кислоты могут быть получены из углеводов. Поэтому при избыточном потреблении углеводов на фоне малоподвижного образа жизни развивается ожирение.

ВРЕМЕННЫЕ УРАВНЕНИЯ СОСТОЯНИЯ И КРИТЕРИИ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ

Вязкие (или реологические) свойства твердых тел устанавливаются главным образом по данным опытов на ползучесть. Ползучестью называется накапливание деформации во времени при постоянном напряжении.

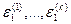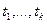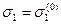Чтобы определить параметры ползучести, достаточно располагать кривой мгновенного деформирования (рис. 49, а) или хотя бы одной кривой ползучести (рис. 49, б). Измерив на кривой ползучести ординаты , соответствующие моментам времени при , откладываем их по оси абсцисс на диаграмме мгновенного деформирования; полученные ординаты обозначаем через 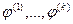. Теперь построим новый график (рис. 49, в). По оси абсцисс отложим 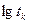, по оси ординат - 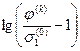. Из соотношения (4.18) должно выполняться равенство

.

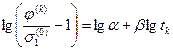Откуда 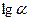- величина отрезка, отсекаемого построенной прямой на оси ординат, а 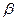- ее угловой коэффициент. Естественно, более точные результаты получатся, если использовать несколько кривых ползучести.

Благодаря простоте и удобству, теория старения нашла широкое применение в практике инженерных расчетов. Но в силу того, что эта теория исходит из опытов на ползучесть при постоянных нагрузках, ею можно пользоваться только в условиях постоянства напряженного состояния или медленного монотонного его изменения.

Для общего случая нагружения твердого тела используют уравнения состояния хорошо разработанной теории наследственной ползучести, достаточно полные сведения о которой можно найти в монографиях [10, 14, 32 и др.].

Ограничимся лишь уравнением состояния линейной теории наследственной ползучести при одноосном упругом сжатии (растяжении) образца переменным во времени напряжении :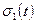

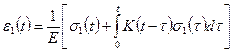(4.20)

или, если известна деформация ползучести 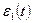, то

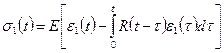, (4.21)

где аналитически связанные функции K(t) и R(t) называются соответственно ядром ползучести и резольвентой ядра ползучести.

Физический смысл функций K(t) и R(t) простой: функция 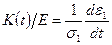- скорость ползучести при постоянном единичном напряжении, а функция 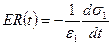- скорость изменяющегося во времени напряжения, необходимого для поддержания постоянной единичной деформации.

Отсюда ясен экспериментальный метод определения функции K(t) по кривой ползучести и R(t) – по релаксационной кривой. Если теория не подвергается сомнению, то необходимость в экспериментальном определении резольвенты отпадает, так как функция R(t) находится аналитически по известному ядру ползучести.

В литературе известно несколько видов ядер ползучести. Наиболее употребляемым является ядро типа Абеля:

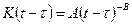, (4.22)

используя которое в уравнении (4.20) при 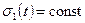, получим уравнение (4.19) теории старения, в котором 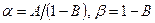. Поэтому из сопоставления уравнений (4.19) и (4.21) легко установить, что резольвентой ядра ползучести (4.22) является функция .

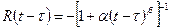Теория наследственной ползучести включает в себя как частные случаи все известные упрощенные теории, например такие, как:

а) релаксационная теория упруговязких сред Максвелла;

б) теория упруговязкой среды Кельвина – Фойгта (модель Кельвина – Фойгта);

в) теория вязкопластичной среды Шведова – Бингама (модель Шведова – Бингама).

Дифференцируя обе части уравнения (4.20) по t и принимая в нем ядро 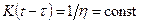, получим уравнение Максвелла

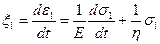. (4.23)

Если в начальный момент времени под действием напряжения 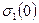деформация образца составила 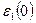и в дальнейшем поддерживается постоянной 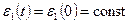, то из уравнения (4.22) следует закон релаксации напряжения

,

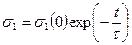где 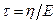называется периодом релаксации напряжений.

При постоянном напряжении ( 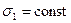) из уравнения (4.23) следует, что тело течет подобно вязкой жидкости.

Аналогично можно получить уравнение Кельвина – Фойгта

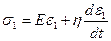
и уравнение Шведова – Бингама

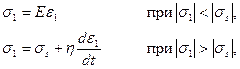
где 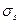- предел текучести (см. рис. 42).

2. Если участок АВ кривой ползучести (см. рис. 46) мал и им можно пренебречь, то применяют теорию установившегося течения, согласно которой скорость ползучести 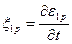в каждый момент времени зависит от напряжения 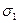при фиксированных внешних условиях, т.е. имеем кинетическое уравнение ползучести

.

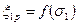Удобными аналитическими аппроксимациями функции 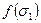являются:

степенная зависимость

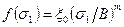, (4.24)

и экспоненциальная

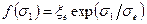, (4.25)

где 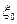- некоторая характерная скорость, которую удобно выбрать за единицу масштаба; 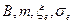- параметры ползучести в условиях опыта.

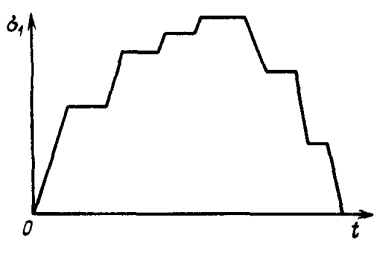
Рис. 50. Характерный вид ступенчатого нагружения образцов при испытаниях их на ползучесть

Экспресс-метод определения параметров ползучести заключается в следующем: серия образцов подвергается ступенчатому нагружению (при фиксированных 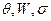) по некоторой программе (рис. 50). На каждой ступени нагружения снимается кривая зависимости деформации от времени, по которой определяется скорость ползучести. Таким образом, для каждого образца (порядковый номер j) получается последовательность из 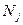точек диаграммы 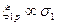(N – число ступеней). Если принять закон ползучести в форме (4.24), то эти точки, нанесенные в координатах 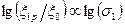, определяют прямую 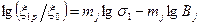. Параметры 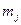и 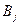для каждого образца находятся методом наименьших квадратов. После этого проводится осреднение полученных характеристик для разных образцов.

Совершенно аналогично находятся параметры экспоненциального закона ползучести (4.25), которому соответствует линейная зависимость .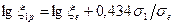

При описании сложно-напряженного состояния по этой теории уравнения (4.8) – (4.10) также справедливы, если в них компоненты деформации 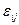заменить компонентами скоростей деформации 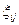и соответственно интенсивность деформации сдвига Г – на интенсивность скоростей деформации сдвига Н, т.е. в общем случае будет

.

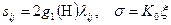Для описания третьего участка кривой ползучести и прогнозирования момента разрушения применяется теория разрушения [32], согласно которой кинетическое уравнение ползучести принимается в виде

,

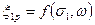где 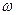- структурный параметр, называемый функцией поврежденности или растрескивания.

Так как повреждение тела начинается на самых ранних этапах деформирования и возрастает с течением времени вплоть до разрушения, то функция 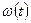должна удовлетворять условиям

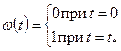, (4.27)

где 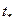- время до начала разрушения.

Накопление повреждений – случайный процесс, и поэтому, согласно представлениям статистической физики, изменение поврежденности можно описать некоторым кинетическим уравнением вида

.

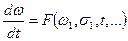Функцию F и параметры процесса определяют экспериментально с привлечением практических и теоретических соображений. При этом существенно, чтобы функция и параметры могли быть найдены из достаточно простых опытов.

Если внешние условия фиксированы и с течением времени структурных изменений нет, то скорость роста поврежденности определяется приведенным напряжением, равным 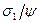, где 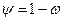- функция сплошности [17]. Тогда процесс ползучести и сопутствующий ему процесс разрушения описывается следующей системой кинетических уравнений:

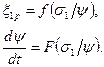
Удобной аппроксимацией функции F является степенная зависимость

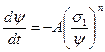, (4.28)

где A > 0 – некоторый коэффициент; 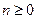- показатель трещинообразования, соответствующий определенным внешним условиям.

Если разрушению предшествуют малые деформации, то можно пренебречь изменением напряжений 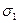во времени и из уравнения (4.28) при условии (4.27) найти время до начала разрушения:

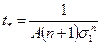(4.29)

Сопоставляя время t с экспериментальным временем разрушения, можно найти параметры A и n. Для этого проводятся испытания на длительную прочность, которые состоят в том, что серия образцов подвергается нагружению различной интенсивности, при этом время разрушения каждого образца фиксируется. Каждому значению напряжения 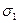соответствует свое время 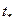. Зависимость между 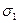и 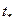называется диаграммой длительной прочности. Она строится в логарифмических координатах.

на втором и третьем участках кривой ползучести накапливаемую деформацию можно вычислить по формуле

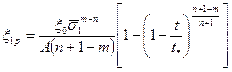(4.30)

сравнение этой зависимости с экспериментальной может служить контролем правильности выбранной аппроксимации.

Время 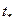, в течение которого исчерпывается несущая способность материала, является наиболее универсальным критерием длительной прочности или долговечностью материала. Наиболее известная в литературе формула для вычисления долговечности

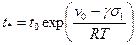(4.31)

получена С.Н. Журковым на основе термофлюктационной концепции для твердых полимеров и пригодна, как утверждается в работе [14], для горных пород. Здесь 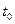- период колебания атомов в твердых телах, для всех полимеров он примерно одинаков и равен 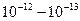с, для горных пород того же порядка; 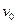- энергия активации процесса термодеструкции; 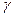- структурно-чувствительный параметр; R – универсальная газовая постоянная Больцмана; T – абсолютная температура. Параметры 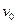и 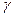определяют по линейной диаграмме длительной прочности в координатах 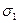и 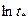. Согласно данным работы [8], для песчаника, песчанистого сланца и глинистых сланцев 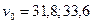и 35 ккал/моль, 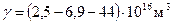соответственно.

Если напряжение 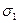зависит от времени, но скорость изменения напряжения невелика, структура и температура материала не изменяются, то согласно принципу суммирования повреждений время до разрушения определится из уравнения [32]

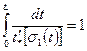, (4.32)

где 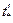- долговечность при постоянном напряжении, равном мгновенному значению .

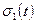В общем случае критерий разрушения имеет вид

.

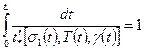Отсюда следует, что в любых условиях механического и теплового воздействия долговечность является функционалом от параметров напряжения, температуры и структуры тела.

В условиях сложного напряженного состояния в уравнениях (4.28) – (4.32) вместо 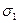необходимо использовать некоторое приведенное напряжение, в качестве которого чаще всего используется интенсивность напряжения 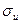[см. формулу (1.41)].