Графоаналитический метод решения уравнения движения машины

Данный метод позволяет не только наглядно иллюстрировать связь между динамическими и кинематическими параметрами движения, но и решать практические задачи синтеза, например, задачу уменьшения неравномерности вращения звеньев.

В качестве примера рассмотрим построение так называемой диаграммы энергомасс. Эта диаграмма строится на основе графиков:

∆Т^пр(φ)=Т^пр(φ)-Т₀^пр(φ) и J^пр(φ),

причем график ∆Т^пр(φ) может быть получен путем графического интегрирования графика М^пр(φ).

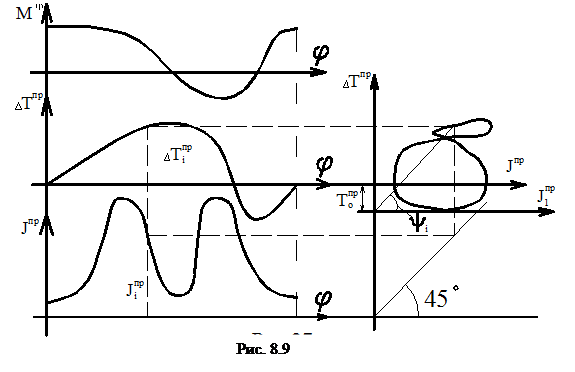
На рис.8.9 показана последовательность построения диаграммы энергомасс в координатах ∆Т^пр(J^пр), которая при установившемся движении является замкнутой кривой и строится на базе диаграмм ∆Т^пр(φ) и J^пр(φ) путем исключения параметра φ (φ – угол поворота звена приведения).

Если известна угловая скорость вращения ω₀ звена приведения в начале цикла, то можно определить начальную кинетическую энергию:Т₀^пр=1/2·J₀^пр·ω₀². Тогда диаграмму энергомасс можно рассматривать в координатах Т^пр(J₁^пр), где ось J₁^пр отстоит от первоначальной оси J^пр на величину Т₀^пр (рис.8.9).

Так как Т^пр=1/2·J^пр·ω², то ω²=2·Т^пр/J^пр=2·μ_Т/μ_J·tgΨ,

где μ_Т и μ_J – масштабные коэффициенты, используемые для построения диаграмм. Таким образом, диаграмма энергомасс позволяет при установившемся движении определить угловую скорость ω звена приведения в любой момент времени, т.е.

ω= 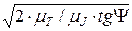; а tgΨ= μ_J/μ_T·ω²/2.