Движение механизма под действием заданных сил. Приведение сил и масс в механизмах.

Задачами динамического анализа и синтеза механизма, машины являются изучение режимов движения с учетом действия внешних сил и установление способов, обеспечивающих заданные режимы движения. При этом могут определяться мощности, необходимые для обеспечения заданного режима движения машины, проводиться сравнительная оценка механизмов с учетом их механического коэффициента полезного действия, устанавливаться законы движения ведущего звена (например, колебания угловой скорости кривошипа за один оборот) под действием внешних сил, приложенных к звеньям механизма, а также решаться задачи подбора оптимальных соотношений между силами, массами, размерами звеньев механизмов.

Анализ движения машинного агрегата, находящегося под действием приложенных к нему внешних сил, удобно проводить с использованием метода приведения масс и сил к какому-либо звену механизма. Он сводится к анализу динамики тела (звена приведения), к которому приведены все внешние силы и моменты. Чаще всего звеном приведения выступает ведущее звено механизма.

Задача динамического анализа – определение истинного закона движения ведущего звена механизма, находящегося под действием заданных внешних сил и моментов, действующих в машинном агрегате.

Кинетическая энергия механизма

Для i-го звена, совершающего сложное движение (например, для шатуна кривошипно-ползунного механизма), кинетическую энергию можно выразить формулой

,

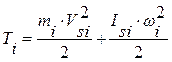где первое слагаемое правой части – это кинетическая энергия поступательного движения центра масс звена; второе слагаемое – кинетическая энергия вращательного движения; m_i – масса звена; V_si – скорость центра масс; J_si – момент инерции звена относительно центра масс; ω_i – угловая скорость звена.

Для всего механизма кинетическая энергия равна сумме кинетических энергий всех звеньев механизма:

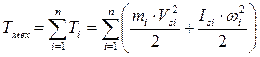, (8.4)

где n – количество подвижных звеньев.

Приведенная масса механизма

Условно заменим механизм его динамической моделью. Например, кривошипно-ползунный механизм (рис. 8.6) заменим динамической моделью, состоящей из стойки и кривошипа.

Здесь ОА – звено приведения механизма, в котором как бы сосредоточена инертность всех звеньев механизма, А – точка приведения.

Уравнение (8.4) умножим и разделим на квадрат скорости точки приведения V_A:

.

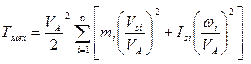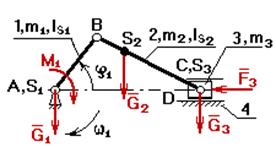
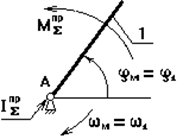
Рис. 8.6. Замена кривошипно-ползунного механизма

динамической моделью

Выражение в квадратных скобках имеет размерность массы (кг) и называется приведенной массой m_пр механизма в точке А.

Тогда

,

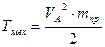где

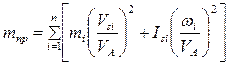. (8.5)

Приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма.

Приведенный момент инерции

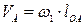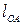Так как , где – длина звена приведения, 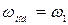– его угловая скорость, то кинетическую энергию механизма можно выразить уравнением

,

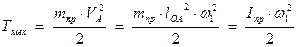где приведенный момент инерции механизма

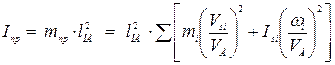. (8.6)

Приведенным моментом инерции механизма называется такой условный момент инерции, которым как бы обладает звено приведения относительно оси вращения, кинетическая энергия которого (при таком моменте инерции) равна сумме кинетических энергий всех звеньев механизма.

Величины m_пр и J_пр не являются постоянными для данного механизма, а меняют свое численное значение в зависимости от положений звеньев, так как звенья меняют свои скорости.

Для исследования закона движения механизма его удобно заменить одним условным звеном – звеном приведения, имеющим закон движения аналогичного звена реального механизма.

Все внешние силы, действующие на звенья при этом заменяются одной приведенной силой F_∑^пр или моментом М_∑^пр , мощности Р_∑^пр которых равны мощностям Р_i заменяемых сил F_i и моментов сил M_i, т.е.

Р_∑^пр=∑Р_i, где Р_i=F_i·V_i·cos(F_iV_i) или Р_i=М_i·ω_i;

Р_∑^пр=F_∑^пр·V·cos(F_∑^прV) или Р_∑^пр=М_∑^пр·ω.

Здесь V_i и V – скорости точек приложения соответствующих сил; ω_i и ω – угловые скорости i-го звена и звена приведения.

Суммарную приведенную силу или момент удобно записывать в виде составляющих, например: М_∑^пр=∑М_Fi^пр+∑М_Мi^пр, где каждая составляющая определяется из соответствующего равенства мощностей:

М_Fi^пр=F_i·V_i/ω·cos(F_iV_i) - для силы F_i;

М_Мi^пр=М_i·ω_i/ω - для момента М_i;

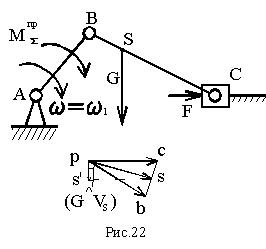
Пример кривошипно-ползунного механизма (рис.8.7): М_∑^пр=М_F^пр+M_G^пр,

где М_F^пр=F·V_C/ω₁=F·l_AB·рс/pb;

M_G^пр=G·V_S/ω₁·cos(G^{^}V_S)=G·l_AB·ps/pb.

Здесь pb, pc, ps^|=ps·cos(G^{^}V_S) – вектора, взятые с плана скоростей (рис.8.7).

Как видно из формул, величина F^пр (М^пр) зависит лишь от соотношения скоростей, а не от их абсолютной величины, что позволяет для приведения сил использовать планы скоростей без учета их масштабов.