Метод Фурье для решения уравнений теплопроводности
Найти функцию 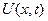 удовлетвор. уравнению
удовлетвор. уравнению
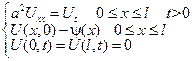
Физически нужно найти распределение температур в стержне длины l, в начальный момент времени 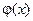 , а на концах нулевая температура
, а на концах нулевая температура
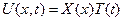 , тогда
, тогда
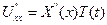
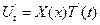
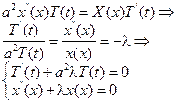
Получены вместо уравнения теплопроодности, два обыкновенных дифференциальных уравнения;
Чтобы получить нетривиальное решение 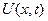 удовлетворяющее однородным граничным условиям, необходима найти нетривиальные решения уравнения:
удовлетворяющее однородным граничным условиям, необходима найти нетривиальные решения уравнения:
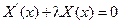 , удовлетворяющее граничным условиям
, удовлетворяющее граничным условиям 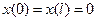
Так же как и при решении однородной краевой задачи для волнового уравнения можно показать, что для
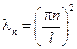
Существует нетривиальное решение 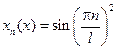 n=1,2,3
n=1,2,3
Постал. задачи Штурман-?
Для решения Т получаем:
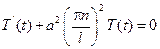
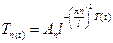
Тогда функции 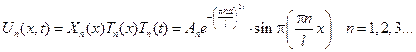 - собственные функции исходной краевой задачи соответствующее собственным значениям
- собственные функции исходной краевой задачи соответствующее собственным значениям
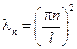 и является соответственным решением исходной краевой задачи; образуем формальный ряд:
и является соответственным решением исходной краевой задачи; образуем формальный ряд:
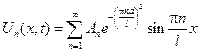 , потребовав, чтобы
, потребовав, чтобы  удовлетвор. начальным условиям
удовлетвор. начальным условиям
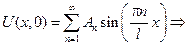
 - коэффициент разложения функции в ряд Фурье по sin на интервале от 0 до n.
- коэффициент разложения функции в ряд Фурье по sin на интервале от 0 до n.
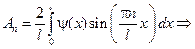
Общее решение
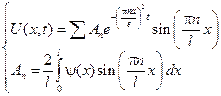
Предположим, что  дважды непрерывно дифферен. на
дважды непрерывно дифферен. на  функции
функции
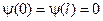 , тогда ряд общего решения будет сходится и функции
, тогда ряд общего решения будет сходится и функции 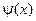 абсолютно и равномерно, поскольку:
абсолютно и равномерно, поскольку:
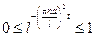
Поэтому сумма этого ряда 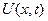 будет непрерывной в области
будет непрерывной в области  ,
,  и удовлетворяет в этой области начальным и граничным условиям.
и удовлетворяет в этой области начальным и граничным условиям.
Рассмотрим общую краевую задачу
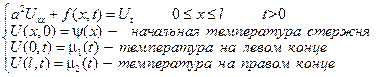
Для того чтобы решить эту задачу будем искать решение в виде:
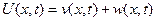 , где
, где
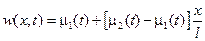
Тогда функция  будет являться решением следующей краевой задачи:
будет являться решением следующей краевой задачи:
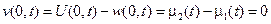
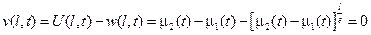
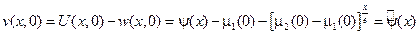 - новое начальное условие для функции
- новое начальное условие для функции 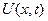
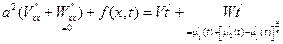
Таким образом функция 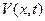 удовлетворяет уравнение:
удовлетворяет уравнение:
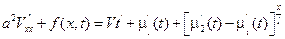
или
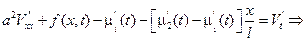
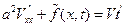
Следовательно, исходная задача упростилась и свелась к нахождению функции 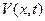
Из следующей краевой задачи
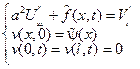
Разобьем ее на 2-е задачи:
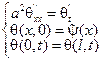
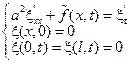
Тогда функция
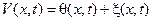
Решаем задачу нахождения функции 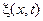 , будем искать решение в виде:
, будем искать решение в виде:
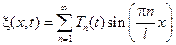
Разложим функцию 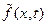 в ряд Фурье по sin на
в ряд Фурье по sin на 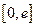 получим:
получим:
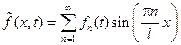 , где
, где
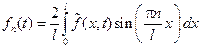
Подставив полученные представления:
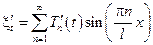
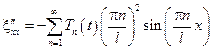
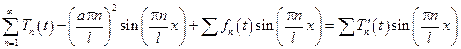
Приравняв соответствующий коэффициент при одинаковых sin, получим бесконечное число уравнений
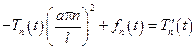
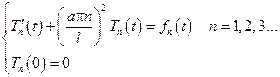
Решение такой задачи, как было показано при решении волновой смешанной задачи, можно представить в виде свертки следующей функции
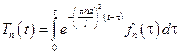
подставляем найденное решение в представлении для функции 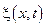 .
.
Найдем 
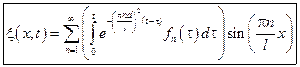 решение 2-ой задачи.
решение 2-ой задачи.
Решение задачи для 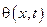
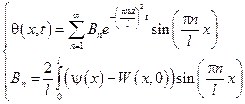 , где
, где
Примеры зад. №18
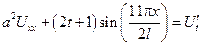
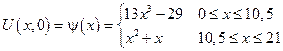
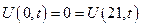
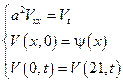
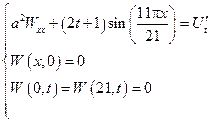
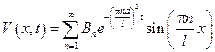
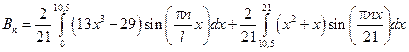
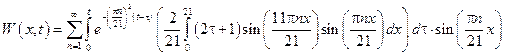 n = 1 – 60
n = 1 – 60
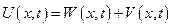
PLOT 3D[
Пример задачи №19
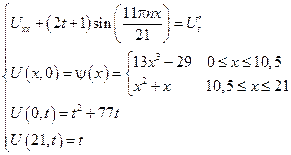
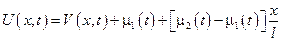
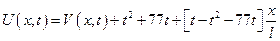
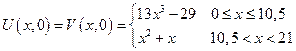
Во всех задачах начальные условия не изменяются.
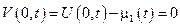
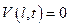
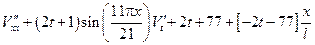
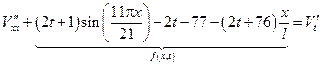
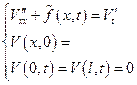
Исходная задача упростилась и свелась к нахождению функции из следующей краевой задачи
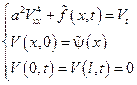
Чтобы решить задачу, разобьем ее на две.
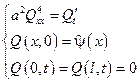
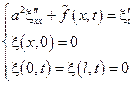
=> 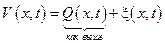
Решим задачу нахождения функции 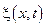 в виде:
в виде:
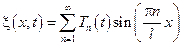
разложим функцию 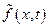 в ряд Фурье по sin на интервале (0,l)
в ряд Фурье по sin на интервале (0,l)
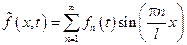 , где
, где
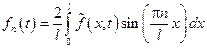
подставим полученные представления:
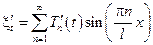
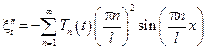
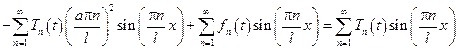
Приравняв
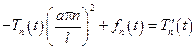 или
или
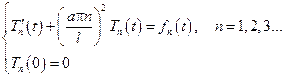
Решение такой задачи, как было показано выше при решении смешанной волновой задачи, можно представить в виде свертки следующей функции.
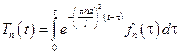
подставляя найденное решение в представлении для функции 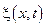 , найдем, что
, найдем, что
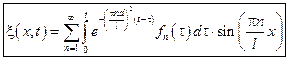
Общее решение.
А решение задачи для нахождения θ было получено ранее и имеет вид.
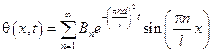 , где
, где
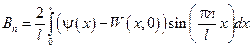
Задача №17: из книги стр. 30 (зад. 5)
Задача №18: в №17 добавить условия.
Пример: (вариант 2)
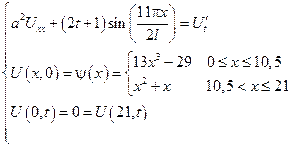
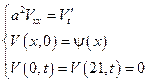
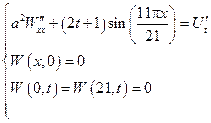
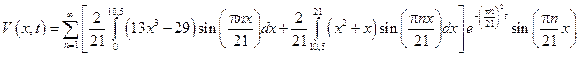
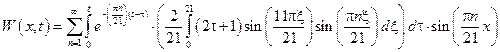
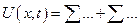
Plot 3D
Задача №19 (вариант 2) Пример:
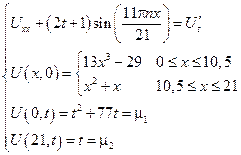
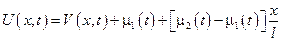
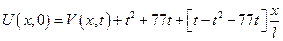
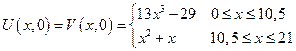
Во всех задачах начальные условия не изменяются.
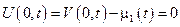
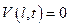
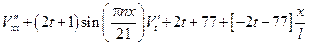
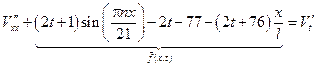
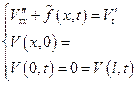
Дата добавления: 2015-02-28; просмотров: 1206;
