Интегральный признак Коши.
Дан ряд с положительными членами 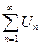 , что
, что 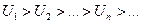 (
( 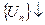 ) и функция f(x) – положительная и убывающая, связанная с рядом равенством f(n)=
) и функция f(x) – положительная и убывающая, связанная с рядом равенством f(n)= 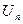 . Тогда несобственный интеграл
. Тогда несобственный интеграл  и
и 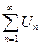 сходится и расходится одновременно.
сходится и расходится одновременно.
Доказательство:
f(n)=Un
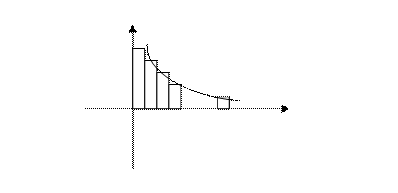
n
S ступенчатой фигуры над рядом (f(x))
 - n частичная сумма ряда.
- n частичная сумма ряда.
S ступенчатой фигуры под графиком функции f(x)
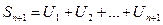 - n+1 частичная сумма ряда.
- n+1 частичная сумма ряда.
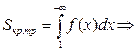 очевидно неравенство
очевидно неравенство 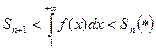
Пусть несобственный интеграл 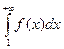 сходится
сходится 
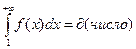
Из левой части 
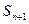 <числа
<числа 

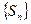 - ограничена сверху числом
- ограничена сверху числом 

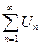 - сходится.
- сходится.
Пусть 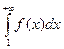 расходится
расходится 
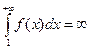
 из правой части (*)
из правой части (*) 
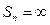

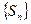 неограничен
неограничен  ряд расходится.
ряд расходится.
Конец доказательства.
Докажем, с помощью интегрального признака Коши, что обобщенно-гармонический ряд:
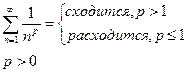
свяжем с эти рядом несобственный интеграл
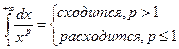 (доказано в несобственном интеграле)
(доказано в несобственном интеграле)  исходный несобственный интеграл сходится или расходится одновременно.
исходный несобственный интеграл сходится или расходится одновременно.
Примеры:
1) 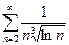
2) 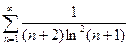
Дата добавления: 2015-01-09; просмотров: 952;
