Вариация признака и технология определения её показателей

Вторая важнейшая задача при определении общего характера распределения – это оценка степени его однородности. Однородность статистических совокупностей характеризуется величиной вариации (рассеяния) признака.

Вариацией признака называют отличие в численных значениях признаков единиц совокупности и их колебания около средней величины, что и будет характеризовать совокупность. Чем меньше вариация, тем более однородна совокупность и более надежна (типична) средняя величина.

Для измерения вариации в статистике используются абсолютные и относительные показатели.

К абсолютным показателям вариацииотносятся:

- размах вариации R,

- среднее линейное отклонение d ,

- средний квадрат отклонений (дисперсия) ,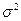

- среднее квадратическое отклонение .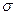

Размах вариации Rявляется наиболее простым показателем вариации, рассчитывается по формуле: R = x _max − x _min

Этот показатель представляет собой разность между максимальным и минимальным значениями признаков и характеризует разброс элементов совокупности. Размах улавливает только крайние значения признака в совокупности, не учитывает повторяемость его промежуточных значений, а также не отражает отклонений всех вариантов значений признака. Размах часто используется в практической деятельности, например, различие между max и min пенсией, заработной платой в различных отраслях и т.д.

Среднее линейное отклонениеd является более строгой характеристикой вариации признака, учитывающей различия всех единиц изучаемой совокупности. Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической. Этот показатель рассчитывается по формулам простой и взвешенной средней арифметической:

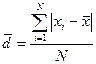- для несгруппированных данных (5.1)

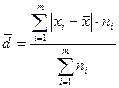- для сгруппированных данных (5.2)

В практических расчетах среднее линейное отклонение используется для оценки ритмичности производства, равномерности поставок.

Так как модули обладают плохими математическими свойствами, то на практике часто применяют другие показатели среднего отклонения от средней – дисперсию и среднее квадратическое отклонение.

Дисперсияпризнака 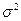представляет собой средний квадрат отклонений вариантов от их средней величины, является общепринятой мерой вариации. В зависимости от исходных данных дисперсия вычисляется по формулам простой и взвешенной средней арифметической:

для несгруппированных данных (5.3)

для сгруппированных данных 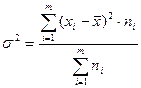(5.4)

При использовании взвешенной средней для расчета дисперсии в интервальных рядах распределения в качестве вариантов значений признака используются серединные значения b (середины интервалов), не являющиеся средним значением в группе. В результате получают приближенное значение дисперсии.

Существуют более простые подходы в вычислении дисперсии.

Наиболее часто используется сокращенный способ расчета дисперсии (метод моментов), в соответствии с которым дисперсия 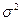есть разницамежду средним из квадратов значений признака 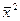и квадратом ихсредней :

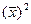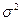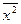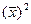= - , где

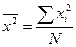- для несгруппированных данных (5.5)

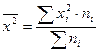- для сгруппированных данных (5.6)

Этот способ позволяет вести расчет дисперсии по исходным данным без предварительного расчета отклонений.

Дисперсия, как базовый показатель вариации, обладает рядом вычислительных свойств, позволяющих упростить её расчет:

- дисперсия постоянной величины равна 0;

- дисперсия не меняется, если все варианты увеличить или уменьшить на одно и то же число А;

- если все варианты умножить (разделить) на число А, то дисперсия увеличится (уменьшится) в A² раз.

Размерность дисперсии соответствует квадрату размерности исследуемого признака, поэтому данный показатель не имеет экономической интерпретации.

Для сохранения экономического смысла рассчитывается ещё один показатель вариации – среднее квадратическое отклонение.

Среднее квадратическое отклонениепредставляет собой среднюю квадратическую из отклонений отдельных значений признака от их средней арифметической:

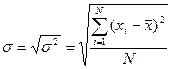для несгруппированных данных (5.7)

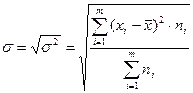для сгруппированных данных (5.8)

Среднее квадратическое отклонение является именованной величиной, имеет размерность усредняемого признака, экономически хорошо интерпретируется. Она также используется для оценки надежности средней: чем меньше cреднее квадратическое отклонение 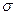, тем надежнее cреднее значение признака x, тем лучше средняя представляет исследуемую совокупность.

Для распределений, близких к нормальным, между средним квадратическим отклонением и средним линейным отклонением существует следующая зависимость:

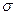≈ 1 , 25 * d (5.9)

Относительные показатели вариациипредназначены для оценки и сравнения вариации нескольких признаков по одной совокупности или же вариации одного и того же признака по нескольким совокупностям. Базой для их исчисления является средняя арифметическая.

Самым распространенным относительным показателем вариации является коэффициент вариации 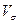. Он представляет собой отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:

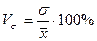(5.10)

Коэффициент вариации используется для характеристики однородности исследуемой совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33% .

Расчет показателей вариации рассмотрим на примере ряда распределения рабочих участка по стажу работы (табл.5.1).

Таблица 5.1 - Расчет показателей вариации для распределения рабочих по стажу работы

№ группы	Стаж работы, лет	ni	ni * xi	Расчет среднего линейного отклонения	Расчет дисперсии
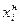
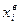
		середина интервала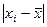
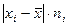
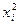
Итого	-					-		-

- Определение среднего стажа работы:

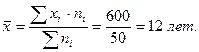
Таким образом, наиболее типичным для рабочих участка является стаж работы, равный 12 годам.

- Определим размах вариации:

R=28-0=28 лет.

Размах вариации показывает общий диапазон изменения стажа, он составляет 28 лет.

- Среднее линейное отклонение составляет

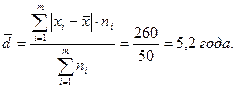
- Дисперсия для данного ряда составляет

= - = -

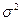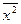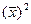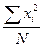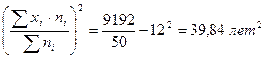
Показатель с такой размерностью невозможно интерпретировать, поэтому рассчитаем среднее квадратическое отклонение

- Среднее квадратическое отклонение составляет 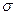= = 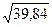6,3 года.

Проверим соотношение между средним линейным отклонением и средним квадратическим отклонением: 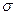≈ 1,25 ⋅ 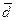≈ 6,5. Можно сделать вывод, что распределение рабочих по стажу близко к нормальному.

- Коэффициент вариации составляет 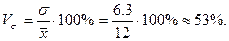свидетельствует о высокой колеблемости признака в совокупности.