Исследование формы распределения элементов совокупности
Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.
Из математической статистики известно, что при увеличении объема статистической совокупности (N → 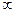 ) и одновременного уменьшении интервала группировки ( хi→ 0) полигон либо гистограмма распределения все более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределенияи представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант.
) и одновременного уменьшении интервала группировки ( хi→ 0) полигон либо гистограмма распределения все более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределенияи представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант.
В статистике различают следующие виды кривых распределения:
- одновершинные кривые;
- многовершинные кривые.
Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки.
Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.
Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях x = Mo = Me .
Для характеристики асимметрии используют коэффициенты асимметрии.
Наиболее часто используются следующие из них:
• Коэффициент асимметрии Пирсона 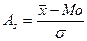 (5.17)
(5.17)
В одновершинных распределениях величина этого показателя изменяется от -1 до +1, в симметричных распределениях As=0.
При As>0 наблюдается правосторонняя асимметрия. В распределениях с правосторонней асимметрией Mo ≤ Me ≤ x .
При As<0 – асимметрия отрицательная левосторонняя, Mo>Me> x .
Чем ближе по модулю As к 1, тем асимметрия существеннее:
- если |As|<0,25, то асимметрия считается незначительной;
- если 0.5 <|As|<0.25 то асимметрия считается умеренной;
- если |As|>0,5 – асимметрия значительна.
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка:
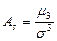 (5.18)
(5.18)
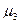 - центральный момент третьего порядка;
- центральный момент третьего порядка;
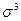 - среднее квадратическое отклонение в третьей степени.
- среднее квадратическое отклонение в третьей степени.
Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.
Центральный момент k-ого порядка рассчитывается как:
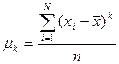 - для несгруппированных данных (5.19)
- для несгруппированных данных (5.19)
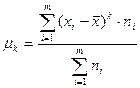 - для сгруппированных данных (5.20)
- для сгруппированных данных (5.20)
Соответственно формулы для определения центрального момента третьего порядка имеют следующий вид:
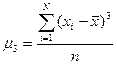 - для несгруппированных данных (5.21)
- для несгруппированных данных (5.21)
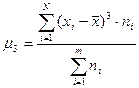 - для сгруппированных данных (5.22)
- для сгруппированных данных (5.22)
Для оценки существенности рассчитанного вторым способом коэффициента асимметрии определяется его средняя квадратическая ошибка:
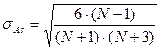 (5.23)
(5.23)
Если 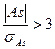 асимметрия является существенной.
асимметрия является существенной.
Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцессявляется показателем островершинности распределения. Он рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка 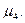
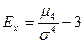
где 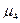 - центральный момент 4-го порядка.
- центральный момент 4-го порядка.
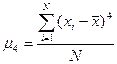 - для несгруппированных данных (5.24)
- для несгруппированных данных (5.24)
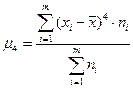 - для сгруппированных данных (5.25)
- для сгруппированных данных (5.25)
При симметричных распределениях Ех=0, если Ех>0, то распределение относится к островершинным, если Ех<0 – к плосковершинным.
Рассчитаем показатели асимметрии и эксцесса для ряда распределения рабочих по стажу работы. Ранее для данного ряда были получены следующие характеристики: x = 12 лет, Мо=12,9 лет, 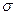 =6,3 года.
=6,3 года.
Коэффициент асимметрии Пирсона получается равным:
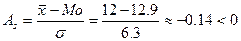 , что говорит о наличии незначительной левосторонней асимметрии в центральной части распределения.
, что говорит о наличии незначительной левосторонней асимметрии в центральной части распределения.
Коэффициент асимметрии, рассчитанный через центральный момент 3-его порядка:
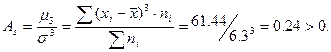
Это означает, что в целом по всему ряду наблюдается правосторонняя асимметрия.
Расчет центрального момента 3- его порядка 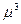 приведен во вспомогательной таблице 5.2.
приведен во вспомогательной таблице 5.2.
Таблица 5.2 - Расчет центральных моментов 3- его и 4-ого порядка
| № | xi | ni | 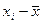
| 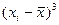
| 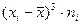
| 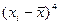
| 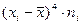
|
| -10 | -1000 | -6000 | |||||
| -6 | -261 | -1728 | |||||
| -2 | -8 | -88 | |||||
| Итого | - | - | - |
Показатель эксцесса:
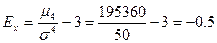 , что свидетельствует о том, что распределение плосковершинное.
, что свидетельствует о том, что распределение плосковершинное.
Дата добавления: 2015-02-25; просмотров: 1288;
