Постановка задачи выборочного исследования

Для постановки задачи выборочного исследования необходимо ввести следующие понятия:

- Генеральная совокупность– изучаемая совокупность, из которой производится отбор единиц, подлежащих изучению, она может быть конечной (N) или бесконечной ( ).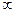

- Выборочная совокупность (выборка)– часть единиц генеральной совокупности, отобранная для изучения (n).

Качество результатов выборочного исследования зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, насколько выборка репрезентативна.

Под репрезентативностьювыборки понимается соответствие ее свойств и структуры свойствам и структуре генеральной совокупности.

Репрезентативность выборки может быть обеспечена только при объективности отбора данных, гарантируемую принципами случайности отбора единиц.

Принцип случайностипредполагает, что на включение или исключение статистической единицы из выборки не может повлиять никакой другой фактор, кроме случая.

Использование методов случайного отбора при формировании выборки позволяет в дальнейшем, при обработке данных, использовать аппарат теории вероятности.

Чаще всего с помощью выборочного исследования определяются следующие характеристики генеральной совокупности:

- Среднее значение признака в совокупности- 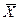, рассчитывается как средняя арифметическая.

- Доля альтернативного признака в совокупности- d .

Альтернативным считается признак, принимающий два значения. Если одно из них изменяется как заданное, то доля альтернативного признака будет характеризовать удельный вес статистических единиц, обладающих заданным значением альтернативного признака, например, доля брака в изготовленной партии продукции;

- Дисперсия признака в совокупности- 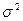, как показатель вариации.

В общем виде задача выборочного исследования формулируется следующим образом:

Пусть имеется некоторая генеральная совокупность известного объема (N единиц), обладающая неизвестными статистическими характеристиками, которыми могут быть:

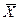- генеральная средняя (среднее арифметическое значение признака в генеральной совокупности).

М – численность единиц, обладающих обследуемым качеством (признаком) в генеральной совокупности.

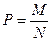- генеральная доля (удельный вес статистических единиц генеральной совокупности, обладающих данным значением признака).

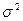- генеральная дисперсия (дисперсия исследуемого признака в генеральной совокупности).

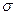- генеральное среднеквадратическое отклонение (среднее квадратическое отклонение исследуемого признака в генеральной совокупности).

Для их определения сформирована выборочная совокупность объемом n статистических единиц (n << N ), обладающая аналогичнымихарактеристиками:

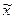- выборочная средняя (среднее арифметическое значение признака в выборочной совокупности).

m – численность единиц, обладающих обследуемым качеством (признаком) в выборочной совокупности

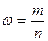- выборочная доля (удельный вес статистических единиц, обладающих данным значением признака в выборочной совокупности).

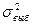- выборочная дисперсия (дисперсия исследуемого признака в выборочной совокупности).

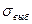– выборочное среднее квадратическое отклонение (среднее квадратическое отклонение изучаемого признака в выборке).

Необходимо на основе известных характеристик выборки получить статистические оценки характеристик генеральной совокупности.