Понятие о малой выборке

При большом числе единиц выборочной совокупности (n >100) распределение случайных ошибок выборочной средней в соответствии с теоремой А.М.Ляпунова нормально или приближается к нормальному по мере увеличения числа наблюдений.

Однако в практике статистических исследований в условиях рыночной экономики все чаще приходится сталкиваться с малыми выборками.

Малой выборкой называетсятакое выборочное наблюдение, численность единиц которого не превышает 30.

Разработка теории малой выборки была начата английским статистиком В.С. ГОССЕТОМ (печатавшимся под псевдонимом СТЬЮДЕНТ). Он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения.

При оценке результатов малой выборки величина генеральной совокупности не используется. Для определения возможных пределов ошибки пользуются критерием Стьюдента, определяемым по формуле:

, (6.20)

где - средняя ошибка малой выборки.

Величина 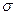вычисляется на основе данных выборочного наблюдения: .

Данная величина используется лишь для исследуемой совокупности, а не в качестве приближенной оценки 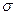в генеральной совокупности.

Предельная ошибка малой выборки ( ) в зависимости от средней ошибки( ) представляется как

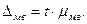
Однако для малой выборки величина коэффициента доверия t по другому связана с вероятностной оценкой, чем при большой выборке (так как, закон распределения отличается от нормального). Согласно установленному Стьюдентом закону распределения, вероятная ошибка распределения зависит как от величины коэффициента доверия t , так и от объема выборки. В таблице 6.4 приведен фрагмент таблицы распределения Стьюдента.

Таблица 6.4 - Распределение вероятностей в малых выборках в зависимости от

коэффициента доверия t и объема выборки

n	t
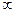
0,5
1,0
1,5
2,0
2,5
3,0

Примечание.1. Для определения вероятности соответствующие табличные значения необходимо разделить на 1000

2.При n = 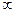приведены вероятности нормального распределения.

Как видно из табл. 3, при увеличении n распределение стремится к нормальному и уже при n = 20практически от него не отличается.

Пример.Предположим, что выборочное обследование 10 рабочих мест малого предприятия показало, что на выполнение одной из производственных операций рабочие затрачивали время (мин.): 3,4; 4,7; 1,8; 3,9; 4,2; 3,9; 3,7; 3,2; 2,2; 3,9.

Алгоритм расчета характеристик малой выборки.

1. Определяем выборочную среднюю затрат времени на выполнение технологической операции:

2. Рассчитываем выборочную дисперсию:

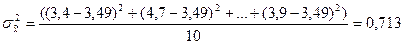
3. Определяем среднюю ошибку малой выборки:

4. Принимаем коэффициент доверия t =2 и по таблице Стьюдента для n =10 вероятность 0,924.

Вывод.С вероятностью 0,924 можно утверждать, что расхождение между выборкой и генеральной совокупностью находится в пределах от 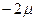до 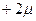,т.е разность не превысит по абсолютной величине значение 0,56(2*0,28). Следовательно, средние затраты времени во всей совокупности будут находится в пределах от 2,93 до 4,05мин. Вероятность того, что данный вывод не буден выполняться равна 1 – 0,924 = 0,076 »7,6 %.