Упражнения и задачи

Задача 6.1

Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование методом случайного бесповтороного отбора. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 10 годам 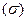. Сколько студентов нужно обследовать, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года?

Задача 6.2

В цехе предприятия 10 бригад рабочих. С целью изучения их производительности труда была осуществлена 20%-ная серийная выборка, в которую попали 2 бригады. В результате обследования установлено, что средняя выработка рабочих в бригадах составила 4,6 и 3 тонн. С вероятностью 0,997 определить пределы, в которых будет находиться средняя выработка рабочих цеха.

Задача 6.3

Методом собственно случайной 10 %-ной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64%, а дисперсия составила 2,56. Определить: 1) среднюю ошибку выборки; 2) с вероятностью, равной 0,954, предельные значения генеральной средней

Задача 6.4

Как изменится величина ошибки бесповторной выборки, если объем увеличится с 5 до 25%.

Задача 6.5

Для определения среднего возраста мужчин, вступающих в брак, в районе была проведена 5%-ная типическая выборка с отбором единиц пропорционально численности типических групп. Внутри групп применялся механический отбор.

Данные по выборке представлены в таблице 6.6:

Таблица 6.6 – Исходные данные

Соц. группа	Число мужчин, ni	Ср. возраст, xi	Среднее квадратическое отклонение,	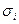Доля мужчин, вступивших во второй брак , %, wi
Рабочие
Служащие

С вероятностью 0,954 определить пределы, в которых будет находиться средний возраст мужчин, вступающих в брак, и долю мужчин, вступающих в брак во второй раз.

Задача 6.6

На основе выборочного обследования методом простой случайной выборки 600 рабочих одной из отраслей промышленности установлено (повторный отбор), что удельный вес численности женщин составил 0,4. С какой вероятностью можно утверждать, что при определении доли женщин, занятых в этой отрасли, допущена предельная ошибка выборки, не превышающая 5%?

Задача 6.7

Среди выборочно обследованных 1000 семей региона по уровню дохода ( выборка 2%-ная, механическая) малообеспеченных оказалось 300 семей. Требуется с вероятностью 0,997 определить долю малообеспеченных семей в регионе.

Задача 6.8

Сколько рабочих завода нужно обследовать в порядке случайной повторной выборки для определения средней заработной платы, чтобы с вероятностью, равной 0,954, можно было бы гарантировать ошибку в размере не более 5 рублей? Предполагаемое среднее квадратическое отклонение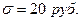

Задача 6.9

Для определения урожайности зерновых культур проведено выборочное обследование 100 хозяйств региона различных форм собственности, в результате которого получены сводные данные (табл. 6.7):

Таблица 6.7 – Исходные данные

Хозяйства	Кол-во обследованных хозяйств (f)	Средняя урожайность, ц/га (xi)	Дисперсия урожайности в каждой группе, ( )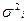
Коллективные
ОАО
Фермерские
Итого

Необходимо с вероятностью 0,954 определить предельную ошибку выборочной средней и доверительные пределы средней урожайности зерновых культур по всем хозяйственным регионам.

Задача 6.10

Для определения среднего срока пользования краткосрочным кредитом в банке было произведена 5%-ая механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определить пределы, в которых будут находиться срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования краткосрочным кредитом более 60 дней.

Задача 6.11

По городской телефонной сети в порядке случайной выборки (механической) отбор произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 5 мин., при среднем квадратическом отклонении 2 мин.

Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 сек.?

Задача 6.12

Для определения зольности угля в порядке случайной выборки было обследовано 100 проб угля. В результате обследования установлено, что средняя зольность угля в выборке 16%, среднее квадратическое отклонение 5%. В десяти пробах зольность угля составила более 20%. С вероятностью 0,954 определить пределы, в которых будут находиться средняя зольность угля в месторождении и доля угля с зольностью более 20%.

Задача 6.13

На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:

Месячный доход, руб. Число рабочих

6000-10000 12

10000-14000 60

14000-18000 20

18000-22000 8

Определить: 1) среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997; 2) долю рабочих предприятия, имеющих месячный доход 14000 руб. и выше, гарантируя результат с вероятностью 0,954; 3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 500 руб.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода 14000 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%.

Задача 6.14

В каком соотношении находится (при прочих равных условиях) ошибки случайной повторной и случайной бесповторной выборок при 10% отборе?

Задача 6.15

Из партии изготовленных изделий общим объемом 2000 единиц проверено посредством механической выборки 30% изделий, из которых бракованными оказались 12 изделий.

Определить: 1) долю бракованных изделий по данным выборки; 2) пределы, в которых находится процент бракованных изделий, для всей партии (с вероятностью 0,954)

Задача 6.16

По данным выборочного обследования 10 000 пассажиров пригородного сообщения средняя дальность поездки пассажира составила 35,5 км, а среднее квадратическое отклонение – 16,0 км.

Определить: 1) пределы средней дальности поездки пассажиров с вероятностью 0,954; 2) как изменится предельная ошибка выборки, если вероятность будет принята равной 0,997?

Задача 6.17

Объем выборки увеличился в 2 раза. Определить, как изменится ошибка простой случайной повторной выборки.

Задача 6.18

Какова должна быть численность механической выборки для определения доли служащих, прошедших повышение квалификации по использованию вычислительной техники, чтобы с вероятностью 0,954 ошибка репрезентативности не превышала 10%? Общая численность служащих предприятия составляет 324 человека.

Задача 6.19

Сколько фирм необходимо проверить налоговой инспекции района, чтобы ошибка доли фирм, несвоевременно уплативших налоги, не превысила 5%? По данным предыдущей проверки, доля таких фирм составила 32%. Доверительную вероятность принять равной 0,954.

Контрольные вопросы

1. Сущность и значение выборочного метода как разновидности несплошного статистического наблюдения.

2. Случаи использования выборочного метода.

3. Проявление закона больших чисел и теории вероятности в выборочном обследовании.

4. Различие повторного и бесповторного отбора.

5. Преимущества выборочного метода как разновидности несплошного статистического наблюдения.

6. Недостатки выборочного метода как разновидности несплошного статистического наблюдения.

7. Виды ошибок в данных выборочного наблюдения.

8. Средняя и предельная ошибки выборки.

9. Показатель доли, расчет средней и предельной ошибок для доли, определение доверительных интервалов.

10. Теоретическое и практическое обоснование объема выборки.

11. Характеристика простой случайной выборки, формулы расчета предельных ошибок и объема выборки.

12. Расслоенная (типическая) выборка, формулы расчета предельных ошибок и объема выборки.

13. Механическая выборка, формулы расчета предельных ошибок и объема выборки.

14. Серийная (гнездовая) выборка, формулы расчета предельных ошибок и объема выборки.

15. Характеристика малой и комбинированной выборок.

Тема №7

Статистическое изучение динамики социально-экономических явлений

и процессов