Показатели анализа рядов динамики
При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут:
- абсолютный прирост,
- темпы роста,
- темпы прироста,
- абсолютное значение одного процента прироста.
Расчет показателей динамики представлен в таблице 7.4.
Таблица 7.4 – Алгоритм расчета показателей динамики
| Показатель | Базисный | Цепной |
Абсолютный прирост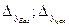 
| Yi-Y0 | Yi-Yi-1 |
| Коэффициент роста (Кр) | Yi : Y0 | Yi : Yi-1 |
| Темп роста (Тр) | (Yi : Y0)×100 | (Yi : Yi-1)×100 |
| Коэффициент прироста (Кпр ) |
| 
|
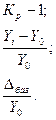
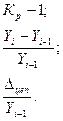
| Темп прироста (Тпр) |
|
|
| Абсолютное значение одного процента прироста (А) |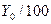 
| 
|
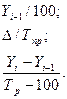
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.
Система средних показателей динамики включает:
средний уровень ряда,
средний абсолютный прирост,
средний темп роста,
средний темп прироста.
Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.
Для интервальных рядов с равными периодами времени средний уровень 
рассчитывается следующим образом:
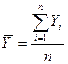(7.1)
где n– общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Yi (1 = 1, 2, ..., n).
Для моментных рядов с равностоящими уровнями средний уровень рассчитывается в предположении, что в пределах каждого периода, разделяющего моментные наблюдения, развитие явления происходило по линейному закону. Тогда общий средний уровень вычисляется по формуле средней хронологической:
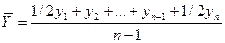(7.2)
Средний абсолютный прирост показывает, на сколько единиц в среднем увеличивался или уменьшался каждый уровень ряда по сравнению с предыдущим за ту или иную единицу времени (в среднем ежемесячно, ежегодно и т.п.).
Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня ряда. Его рассчитывают в зависимости от исходных данных следующими способами:
1) как простую среднюю арифметическую из абсолютных приростов (цепных) за последовательные промежутки времени: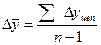 
(7.3)
2) как частное от деления базисного абсолютного прироста конечного уровня ряда на продолжительность периода: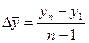 
(7.4)
3) через накопленный (базисный) абсолютный прирост: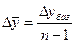 
(7.5)
Средний коэффициент роста (снижения)показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Для его вычисления используется формула средней геометрической в предположении, что соблюдается равенство фактического отношения конечного уровня к начальному при замене фактических темпов на средние. В зависимости от наличия исходных данных расчет проводят следующим образом:
1) если исходной информацией служат цепные коэффициенты роста, то формула имеет вид: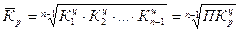 
, где П – произведение цепных показателей динамики.
2) Через базисный коэффициент роста конечного периода: 
(7.6)
3) Если известны уровни динамического ряда: 
(7.7)
Средний темп ростапредставляет собой средний коэффициент роста, выраженный в процентах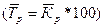 
. Отсюда средний темп прироста 
.
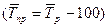Пример.
Имеются следующие данные (табл. 7.5) о производстве хлеба и хлебобулочных изделий в регионе за сутки:
Таблица 7.5 – Исходные данные
| Хлеб и хлебобулочные изделия, т |
Определить показатели динамики производства хлеба и хлебобулочных изделий от года к году и средние за весь анализируемый период.
Решение:
| Наименование показателя | Год | ||||
Абсолютный прирос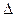т  , т
| с переменной базой | - |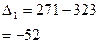 
| 
| 
|
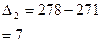
| с постоянной базой | - |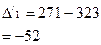 
| 
| 
| |
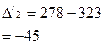
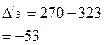
| Коэффициент роста (Кр) | с переменной базой | - |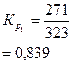 
| 
| 
|
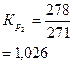
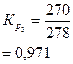
| с постоянной базой | - |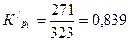 
| 
| 
| |
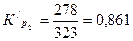
| Темп роста, Тр, % | с переменной базой | - |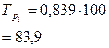 
| 
| 
|
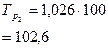
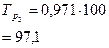
| с постоянной базой | - | 
| 
| 
| |
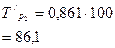
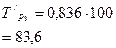
| Темп прироста, Тпр, % | с переменной базой | - |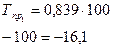 
| 
| 
|
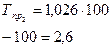
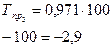
| с постоянной базой | - | 
| 
| 
| |
| Абсолютное значение 1% прироста (снижения) А, т | с переменной базой | - |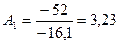 
| 
| 
|
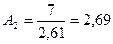
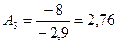
| с постоянной базой | - | 
| 
| 
|
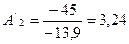
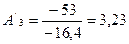
Средняя величина абсолютного значения 1% прироста (снижения):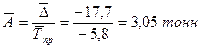 
Средний уровень интервального ряда динамики:
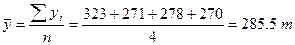
Средний абсолютный прирост:
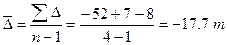
Средний коэффициент роста:
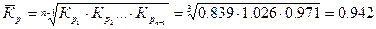
или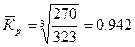 
Средний темп роста: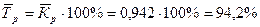 
Средний темп прироста: 
Дата добавления: 2015-02-25; просмотров: 1317;