Числовые ряды с положительными членами

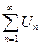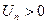Рассмотрим знакоположительный числовой ряд , где .Последовательность частичных сумм такого ряда будет всегда возрастающей:

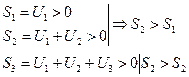
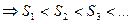
На 1 курсе была доказана теорема о том, что: монотонно возрастающая последовательность, ограниченная сверху имеет конечный предел.

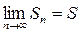- число.

Для знакоположительного ряда достаточно доказать, что, последовательность частичных сумм 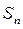ограничена сверху числом (возрастание и так есть).