Й признак сравнения
Дано 2 ряда с положительными членами 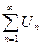 (1) и
(1) и 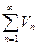 (2) и начиная с некоторого номера N выполняется неравенство
(2) и начиная с некоторого номера N выполняется неравенство 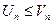 , тогда если (2) сходится то и (1) сходится. Если (1) расходится то и (2) тоже расходится, (ряд меньший сходящегося тоже сходится, ряд больший расходящегося тоже расходится).
, тогда если (2) сходится то и (1) сходится. Если (1) расходится то и (2) тоже расходится, (ряд меньший сходящегося тоже сходится, ряд больший расходящегося тоже расходится).
Доказательство: Обозначим через 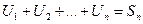 - n – частичная сумма 1 ряда и
- n – частичная сумма 1 ряда и 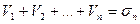 - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
Т.к 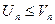
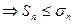 . Пусть 2 ряд сходится, тогда
. Пусть 2 ряд сходится, тогда 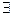
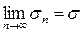 , причём
, причём 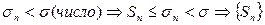 ограничена сверху числом
ограничена сверху числом 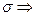 (1) сходится.
(1) сходится.
Пусть 1 ряд расходится 
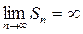 , т.к
, т.к 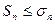

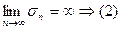 расходится.
расходится.
Конец доказательство.
Замечание:при доказательстве этого признака мы считали, что неравенство 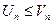 выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
Для сравнения необходим стандартный набор рядов, о сходимости всё известно. К таким рядам относятся:
| Ряды для сравнения: | |
Ряды членов геометрической прогрессии:
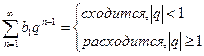
| Обобщенно гармонический ряд:
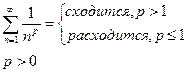 (строгое доказательство будет проведено после интегрального признака сходимости)
(строгое доказательство будет проведено после интегрального признака сходимости)
|
Примеры:
1) 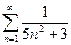
2) 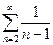
3) 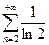
II признак сравнения (предельный)
Дано 2 ряда с положительными членами 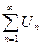 (1) и
(1) и 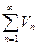 (2) и
(2) и 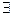
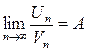 - число
- число 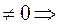 (1) и (2) сходятся и расходятся одновременно.
(1) и (2) сходятся и расходятся одновременно.
Доказательство:
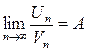 - число
- число  по определению предела последовательности:
по определению предела последовательности:
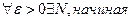 с которого
с которого 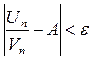
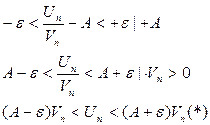
Пусть (2) сходится , тогда сходится и 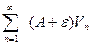

Из правой части 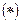 следует, что (1) ряд меньше сходящегося ряда
следует, что (1) ряд меньше сходящегося ряда  по 1 признаку сравнения
по 1 признаку сравнения  (1) сходится
(1) сходится
Пусть (2) расходится  выберем
выберем 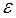 настолько малым, чтобы
настолько малым, чтобы 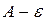 оставалось >0, для знакоположительности ряда
оставалось >0, для знакоположительности ряда 
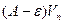 - расходится. Из левой части (*)
- расходится. Из левой части (*)  (1) ряд>ряда расходящегося по I признаку сравнения (1) ряд расходится.
(1) ряд>ряда расходящегося по I признаку сравнения (1) ряд расходится.
Конец доказательства.
Примеры:
1) 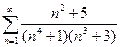
2) 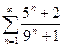
3) 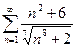
Дата добавления: 2015-01-09; просмотров: 1028;
