Анализ связи между атрибутивными признаками
Использование регрессионного и корреляционного анализа требует, чтобы все признаки были количественно измеренными. Методы КРА, основанные на использовании количественных параметров распределения (средние величины, дисперсия), называют параметрическими методами.
Вместе с тем в статистике, особенно при проведении социологических исследований, возникает потребность оценки тесноты связи между качественными (атрибутивными) признаками. Проблему оценки тесноты связи между атрибутивными признаками решают непараметрические методы. Сфера их использования значительно шире в сравнении с параметрическими методами, потому что не требует использования условия нормального распределения результативной переменной, не ставится задача представления зависимости между атрибутивными признаками соответствующим уравнением. Здесь речь идет только о наличии установления связи и измерения его тесноты.
Взаимосвязь между атрибутивными признаками анализируется посредством таблиц взаимной сопряженности. Они описывают комбинационные распределения совокупности по факторному признаку х и результативному у.
Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.
| Занятия родителей | Число детей, занятых в | Всего | |||
| промышлен- ности и стро- ительстве | сельском хозяйстве | сфере обслужи- вания | сфере интел- лектуального труда | ||
| 1. Промышленность и строительство | |||||
| 2. Сельское хозяйство | |||||
| 3. Сфера обслуживания | |||||
| 4. Сфера интеллектульного труда | |||||
| Всего |
Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 («Промышленность и строительство») заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т.д.
Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т.д.
Однако важно получить обобщающие показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях.
При наличии стохастической связи оценка ее тесноты базируется на отклонениях фактических частот fij от Fij, пропорциональных итоговым частотам:
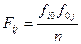 , (9.11)
, (9.11)
где fi0-суммарные частоты по признаку х; f0j - суммарные частоты по признаку у; n – объем совокупности.
Абсолютную величину отклонений фактических частот fij от пропорциональных Fij (fij - Fij) характеризуют статистическим критерием 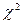 .
.
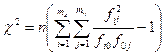 . (9.12)
. (9.12)
При отсутствии стохастической связи 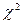 =0. Для вывода о тесноте связи теоретическое значение
=0. Для вывода о тесноте связи теоретическое значение 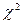 сравнивают с табличным
сравнивают с табличным 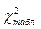 и делают вывод о наличии тесной связи между признаками х и у.
и делают вывод о наличии тесной связи между признаками х и у.
Относительной мерой тесноты стохастической связи между признаками служат также:
- коэффициент взаимной сопряженности Чупрова
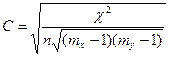 ; (9.13)
; (9.13)
- коэффициент взаимной сопряженности Крамера (при mx 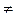 my).
my).
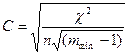 , (9.14)
, (9.14)
где mmin – минимальное число групп (mx или my).
Значение коэффициент С колеблется от 0 до 1 и теснота связи тем сильнее, чем более близко С к 1.
Достаточно часто в практике статистических исследований анализируются связи между альтернативными признаками, которые представлены группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценивать посредством коэффициента ассоциации Д.Юла и коэффициента контингенции К.Пирсона.
Для расчета указанных коэффициентов измерения тесноты связи между альтернативными признаками используется таблица взаимной сопряженности в виде корреляционной таблицы, которая носит название «четырехклеточной таблицы».
Таблица 9.1 - Таблица взаимной сопряженности
| a | b | a+d |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
При использовании таблицы 10.1 с частотами a,b,c,d коэффициент ассоциации (Ка) вычисляется по формуле:
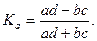 (9.15)
(9.15)
При Ка>0,3 между изучаемыми качественными признаками существует корреляционная связь.
В случаях, когда один из показателей четерехклеточной таблицы отсутствует, величина коэффициента ассоциации будет равняться единице, что дает завышенную оценку тесноты связи между признаками. В этом случае необходимо рассчитывать коэффициент контингенции (Кk):
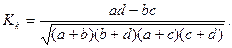 (9.16)
(9.16)
Коэффициент контингенции находится в диапазоне от -1 к +1. Чем более близок Kk к (+1) или (-1), тем теснее связь между изучаемыми признаками. Коэффициент контингенции всегда меньше коэффициента ассоциации.
Для определения связи как между количественными, так и между качественными признаками при условии, что значения этих признаков упорядочены по степени уменьшения или увеличения (ранжированные), может быть использован коэффициент корреляции рангов Спирмена. Рангами называют числа натурального ряда, которые представляются в баллах по определенным критериям элементов совокупности. При этом ранжирование проводится по каждому признаку отдельно: первый ранг предоставляется наименьшему значению признака, последний – наибольшему. Количество рангов равняется объему совокупности. Преимуществом этого подхода является то, что при отсутствии требования нормального распределения ранговые оценки тесноты связи целесообразно использовать для совокупности небольшого объема.
Показатель ранговой корреляции – коэффициент корреляции рангов Спирмена – рассчитывается по формуле:
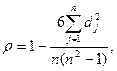 (9.17)
(9.17)
где 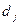 - разность между рангами по одному и другому признаку (
- разность между рангами по одному и другому признаку ( 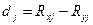 );
);
n – количество единиц в ряду.
Если 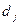 =0, то
=0, то 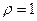 - существует тесная прямая связь. Если первому рангу по размеру одного признака соответствует последний ранг по размеру второго признака, второму рангу – предпоследний ранг второго признака и т.п., то
- существует тесная прямая связь. Если первому рангу по размеру одного признака соответствует последний ранг по размеру второго признака, второму рангу – предпоследний ранг второго признака и т.п., то 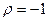 и существует тесная обратная связь. Если значение
и существует тесная обратная связь. Если значение 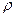 близко к нулю, то связь слабая или ее вообще нет.
близко к нулю, то связь слабая или ее вообще нет.
Дата добавления: 2015-02-25; просмотров: 2381;
