Упражнения и задачи. Имеются следующие данные (табл
Задача 8.1
Имеются следующие данные (табл. 8.1) о производстве хлеба и хлебобулочных изделий предприятиями Брянской области, тыс. тонн:
Таблица 8.1 - Производство хлеба и хлебобулочных изделий предприятиями Брянской области
| Хлеб и хлебобулочные изделия | 140,6 | 131,6 | 121,4 | 117,8 | 118,3 | 108,8 | 101,4 | 98,4 | 95,1 | 90,9 |
Определите индивидуальные индексы объема продукции: 1) цепным способом; 2) базисным способом, приняв за базу сравнения 1995 год; 3) выполните проверку расчета базисных индексов.
Задача 8.2
Определите, как изменились в среднем отпускные цены на продукцию, если количество произведенной продукции в отчетном периоде по сравнению с базисным увеличилось на 8,0%, а общая стоимость продукции уменьшилась на 5,0%.
Задача 8.3
Имеются следующие данные (табл. 8.2):
Таблица 8.2 – Исходные данные
| Виды изделия | Себестоимость 1 шт., руб. | Произведено, тыс. шт. | Индивидуальные индексы | |||
| базисный период | отчетный период | базисный период | отчетный период | базисный период | отчетный период | |
| А | ? | 1.2 | 1.31 | 0.92 | ? | |
| Б | ? | 3.0 | ? | 0.71 | ||
| В | ? | 0.72 | ? | 0.99 | 2.92 |
Определите: а) недостающие показатели в таблице; б) сводные индексы цен физического объема продукции (взвешенные по себестоимости) и затрат на производство.
Задача 8.4
Имеются данные (табл. 8.3) о реализации помидоров магазином:
Таблица 8.3 – Исходные данные
| Месяц | Цена за 1 кг, руб. | Продано, кг. |
| Июнь | 45,0 | |
| Сентябрь | 18,0 | |
| Октябрь | 35,0 |
Определите цепные и базисные индексы цен, физического объема продажи и товарооборота, покажите взаимосвязь между ними.
Задача 8.5
Имеются данные (табл. 8.4) о продаже сельскохозяйственной продукции на рынке города:
Таблица 8.4 – Исходные данные
| Товары | Продано за период, т | Средняя цена за 1 кг в течение периода, д.е. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Картофель | 1,00 | 4,20 | ||
| Морковь | 1,30 | 5,50 | ||
| Свёкла | 1,20 | 5,30 | ||
| Капуста | 0,80 | 4,60 | ||
| Лук | 1,50 | 8,00 |
Определите: 1) агрегатные индексы физического объема продукции, цен, стоимости (товарооборота); 2) абсолютный прирост (уменьшение) стоимости проданных товаров в результате изменения цен в текущем периоде.
Задача 8.6
Имеются данные (табл. 8.5) об объеме произведенной продукции и ее себестоимости на предприятии.
Таблица 8.5 – Исходные данные
| Продукция | Объем произведенной продукции, тыс. шт. | Себестоимость продукции, д.е. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| А | 3,1 | 3,3 | 1,1 | 1,2 |
| Б | 5,2 | 5,8 | 0,9 | 0,8 |
Определите: 1) индивидуальные индексы и агрегатные индексы физического объема продукции, себестоимости, расходов на производство продукции; 2) экономический эффект от снижения себестоимости продукции.
Задача 8.7
Имеются данные (табл. 8.6) о реализации продукции торговым предприятием:
Таблица 8.6 – Исходные данные
| Товары | Объем потребления отчетного периода, тыс.д.е. | Индексы цен ip |
| Мясопродукты | 315,0 | 1,05 |
| Молочные продукты | 26,5 | 0,95 |
| Хлебопродукты | 32,8 | 0,98 |
| Всего | 374,3 | х |
Определите общий индекс цен.
Задача 8.8
Имеются данные (табл.8.7) по сельскохозяйственным предприятиям о реализованной продукции в базисном периоде и изменениям в объеме продукции в текущем периоде:
Таблица 8.7 – Исходные данные
| Продукция | Стоимость продукции в базисном периоде, тыс. д.е. | Изменение объема продукции в текущем периоде по сравнению с базисным |
| Зерно | +11% | |
| Картофель | -3% | |
| Овощи | Без изменений | |
| Всего | х |
Необходимо определить общий индекс физического объема продукции.
Задача 8.9
Имеются исходные данные (табл. 8.8) о количестве, ценах и стоимости реализованной продукции:
Таблица 8.8 – Исходные данные
| Виды продукции | Количество реализованной продукции, тыс.ед. | Цена единицы продукции, руб. | Стоимость реализованной продукции, тыс.руб. | ||||
| q0 | q1 | p0 | p1 | q0 p0 | q1 p0 | q1 p1 | |
| А | |||||||
| Б | |||||||
| В | |||||||
| Итого | х | х | х | х |
Определите: 1) в относительном и абсолютном выражении изменение стоимости реализованной продукции в отчетном периоде по сравнению с базисным периодом; 2) в какой мере это изменение вызвано изменением: а) количества реализованной продукции; б) цен разнородной продукции.
Задача 8.10
На основании данных задачи 8.9 определите:
1) индивидуальные индексы количества продукции;
2) индивидуальные индексы изменения цен;
3) средний взвешенный индекс количества продукции;
4) средневзвешенный индекс цен.
Задача 8.11
Имеются данные (табл. 8.9) о количестве, ценах, себестоимости и массе прибыли.
Таблица 8.9 – Исходные данные
| Вид продукции | Количество, тыс.шт. | Цена ед. продукции, руб. | Себестоимость ед. продукции, руб. | |||
| q0 | q1 | p0 | p1 | z0 | z1 | |
| А | ||||||
| Б | ||||||
| В |
Определите:
1) изменение прибыли в отчетном периоде по сравнению с базисным в относительном и абсолютном выражении;
2) изменение прибыли за счет изменения: а) количества продукции (физического объема); б) структуры реализованной продукции; в) цен реализованной продукции; г) себестоимости продукции.
3) Установление взаимосвязи в относительном и абсолютном выражении.
Задача 8.12
Имеются данные (табл. 8.10) о численности работников и фонде заработной платы предприятия:
Таблица 8.10 – Исходные данные
| № цеха | Численность работников | Фонд заработной платы, тыс.руб. | ||
| базисный период Т0 | отчетный период Т1 | базисный период Т0f0 | отчетный период Т1f1 | |
| Итого |
Определите:
1) среднюю заработную плату в целом по предприятию в базисном и отчетном периодах;
2) изменение средней заработной платы в отчетном периоде по сравнению с базисным в относительном и абсолютном выражении;
3) в какой мере оказало влияние на изменение средней заработной платы: а) изменение структуры работников; б) изменение заработной платы в отдельных цехах.
Задача 8.13
Как в среднем изменились цены на молочную продукцию, если известно, что объем реализации за период увеличился на 15%, а товарооборот по этой группе товаров увеличился на 21%.
Контрольные вопросы
1. Назовите задачи, которые решают с помощью индексов.
2. Перечислите основные элементы индексов.
3. Какие индексы бывают по форме построения?
4. Какие индексы бывают по базе сравнения?
5. Что означает в теории индексов параметр q?
6. Что означает в теории индексов параметр р?
7. Как исчисляют агрегатные и средние из индивидуальных индексы цен?
8. Какие формы средних используются при расчете средних индексов?
9. Где нашли наибольшее применение средние индексы?
10. Как определить агрегатный индекс цен по формуле Пааше?
11. Как определить агрегатный индекс цен по формуле Ласпейреса?
12. Как определить индекс товарооборота?
13. Что выражает индекс переменного состава?
14. Что выражает индекс постоянного состава?
15. Что характеризует индекс физического объема продукции?
16. Расскажите о взаимосвязи между индексами переменного, постоянного состава и структуры.
Тема №9
Статистическое изучение взаимосвязи социально-экономических явлений
Основные понятия корреляционного и регрессионного анализа
Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и стохастическую (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и объемом произведенной продукции.
Стохастическая связь (которую также называют неполной, или статистической), когда каждому отдельному значению факторного признака х отвечает определенное множество значений результативного признака у.
Разновидностью стохастической связи является корреляционная зависимость, которая предопределяет корреляционную зависимость между признаками. При такой зависимости с изменением факторного признака х изменяются групповые средние результативного признака у и вместо условных распределений множеств значений признака у выступают средние значения этих распределений 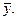 Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается – увеличение массы внесенных удобрений ведет к росту урожайности.
По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать, соответственно, положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные – множественной.
Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но кроме перечисленных различают также непосредственные, косвенные и ложные связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.
Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле – когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле – когда исследуется сила связи – и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие.
Задачи собственнокорреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Задачирегрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.
Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.
Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.
Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы – параметрические – и принято называть корреляционными.
Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений.
Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы:
| \ Y \ X \ | Y1 | Y2 | ... | Yz | Итого | Yi |
| X1 | f11 | ... | f1z | 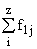
| 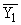
| |
| X2 | f21 | ... | f2z | 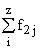
| 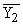
| |
| ... | ... | ... | ... | ... | ... | ... |
| Xk | fk1 | k2 | ... | fkz | 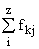
| 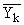
|
| Итого | 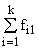
| 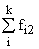
| ... | 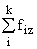
| n | 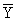
|
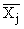
| 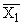
| 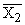
| ... | 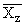
| 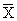
| - |
В основу группировки положены два изучаемых во взаимосвязи признака – Х и У. Частоты fij показывают количество соответствующих сочетаний Х и У. Если fij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания fij допустимо утверждать о связи между Х и У. При этом, если fij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь.
Корреляционная связь между признаками х и у записывается в виде уравнения корреляционной связи, или уравнения регрессии:
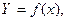
где f(x) – определенный вид функции корреляционной связи, которая описывает линию регрессии.
Определение корреляционной связи между признаками занимает важное место в исследованиях социально-экономических явлений в экономике и управлении. Содержание такой связи отражает теория корреляции. Основоположником этой теории являются английские ученые-биологи Ф.Гамильтон и К.Пирсон. Термин «корреляция» заимствован из естествознания и означает соотношение, соответствие между переменными в уравнении регрессии.
В основе теории корреляции лежит корреляционно-регрессионный анализ (КРА), суть которого заключается в выборе вида уравнения регрессии, вычислении его параметров и установлении адекватности (соответствия) теоретической зависимости фактическим данным, представленным в табличной форме. Наличие такой теоретической зависимости значительно облегчает анализ экономических явлений, дает возможность установления прогноза на будущее.
Дата добавления: 2015-02-25; просмотров: 1990;
