Общие индексы средних величин
В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие характеристики качественных показателей как средняя цена, средняя себестоимость, средняя производительность труда и др. Так как на динамику средней влияют не только изменения осредняемого признака, но и изменения состава рассматриваемой совокупности. Влияние каждого из этих факторов оценивается посредством общих индексов средних величин. Такие индексы образуют индексную систему, которая для качественных показателей состоит из трех элементов: индексов переменного состава 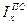 ; индексов фиксированного (постоянного) состава
; индексов фиксированного (постоянного) состава 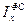 ; индексов структурных сдвигов
; индексов структурных сдвигов 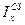 , где х – вид рассматриваемого признака (цена, себестоимость, производительность труда и т.п.).
, где х – вид рассматриваемого признака (цена, себестоимость, производительность труда и т.п.).
Индекс переменного состава 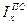 показывает относительное изменение рассматриваемого среднего уровня признака в целом за счет двух факторов – изменения индексируемого признака и изменения в структуре совокупности:
показывает относительное изменение рассматриваемого среднего уровня признака в целом за счет двух факторов – изменения индексируемого признака и изменения в структуре совокупности:
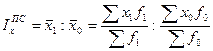 , (8.16)
, (8.16)
где 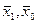 - средние признаки соответственно в текущем и базисном периодах;
- средние признаки соответственно в текущем и базисном периодах; 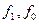 - веса признака в сопоставимых периодах.
- веса признака в сопоставимых периодах.
Для разных качественных показателей индекс переменного состава можно записать в виде следующих отношений:
1) Индекс себестоимости переменного состава: 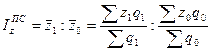 . (8.17)
. (8.17)
2) Индекс цен переменного состава: 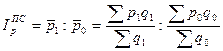 . (8.18)
. (8.18)
3)Индекс производительности труда переменного состава: 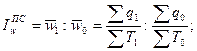
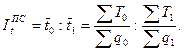 (8.19)
(8.19)
Свое название (переменного состава) эти индексы получили потому, что средние величины, динамику которых они отражают, могут меняться не только за счет изменения данного индексируемого показателя, но и за счет изменения удельного веса данных показателей в общей совокупности (т.е. изменения ее состава). Например, средняя себестоимость определенного вида продукции, выпускаемой разными предприятиями, зависит не только от уровня себестоимости на отдельных предприятиях, но и от количества продукции, выпускаемой этими предприятиями. Поэтому индекс себестоимости переменного состава отражает изменение средней себестоимости определенной продукции, как за счет изменения себестоимости на отдельных предприятиях, так и за счет изменения удельного веса отдельных предприятий в общем объеме выпускаемой продукции. Аналогично, индекс цен переменного состава показывает как изменилась средняя цена отдельного вида продукции, реализуемой по разным ценам разными предприятиями за счет изменения цен и за счет изменения доли продукции, реализуемой этими предприятиями. Индекс производительности труда переменного состава показывает изменение средней производительности труда, как за счет ее изменения на отдельных предприятиях, так и за счет перераспределения рабочих (изменения их численности) на этих предприятиях.
Следовательно, все индексы переменного состава наряду с изменениями индексируемого показателя отражают влияние изменения состава (структуры) той совокупности, для которой рассчитаны средние.
Индекс фиксированного (постоянного) состава 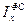 характеризует изменение среднего уровня за счет изменения только индексируемой величины при той же структуре совокупности (соизмерители неизменны):
характеризует изменение среднего уровня за счет изменения только индексируемой величины при той же структуре совокупности (соизмерители неизменны):
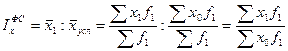 . (8.20)
. (8.20)
Индекс структурных сдвигов 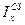 показывает изменение среднего уровня показателя за счет изменений в структуре совокупности при неизменном значении признака:
показывает изменение среднего уровня показателя за счет изменений в структуре совокупности при неизменном значении признака: 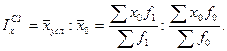 (8.21)
(8.21)
Формулы для средних индексов подчиняются принципу взаимозависимости, который обеспечивает их сведение в индексную систему: 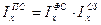 . С использованием этой формулы по двум известным индексам можно рассчитать третий.
. С использованием этой формулы по двум известным индексам можно рассчитать третий.
На основе вышеприведенных формул можно рассчитать абсолютное изменение среднего уровня вторичного признака за счет отдельных факторов – самого усредняемого признака 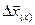 и структуры
и структуры 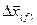 :
: 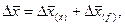 где
где 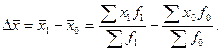
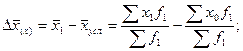
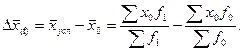
Влияние структурных сдвигов на изменение среднего уровня изучаемого явления особенно заметно при сравнениях за длительные периоды времени и в условиях существенных изменений в структуре социально-экономических процессов. В связи с этим исключение воздействия структурного фактора при анализе изменений средних значений признаков как показателей основной тенденции – это необходимое условие для получения реалистичной оценки и правильных выводов на основе индексного анализа различных сложных явлений.
Например, сравнение показателей рождаемости и смертности населения за 10-летний период без учета изменении в половозрастной структуре населения приведет к искаженной оценке динамики этого показателя, так как его средние значения несопоставимы между собой вследствие различий в структурах изучаемых совокупностей. В таких случаях анализируемые показатели нужно рассчитывать по одинаковой, стандартной половозрастной структуре населения. Используемый в демографии для этих целей метод стандартизации показателей рождаемости и смертности по сути является методом построения индекса постоянного состава.
Пример.
Имеются данные о выпуске продукции предприятиями отрасли.
| Номер предприятия | Выпуск продукции, тыс.шт. | Цена реализации единицы продукции, д.е. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| q0 | q1 | р0 | р1 | |
| 47,15 | 50,25 | |||
| 46,05 | 47,20 | |||
| 50,00 | 51,80 | |||
| 51,90 | 52,90 | |||
| 47,90 | 46,40 | |||
| Всего | х | х |
Определите: 1) индексы цен переменного и постоянного состава, структурных сдвигов; 2) абсолютный прирост средней цены, прирост цены в результате изменений самих цен и структурных сдвигов; 3) абсолютный рост стоимостного объема реализации в результате роста средней цены, в том числе в результате изменений цен на отдельных предприятиях и изменения структуры реализованной продукции.
Решение:
1. Вычислим индекс цен переменного состава, который выражает изменение средней цены реализации с учетом двух факторов: как в результате изменения самих цен реализации продукции конкретными предприятиями, так и изменения структуры в реализации продукции, т.е. удельного веса отдельных предприятий в общем объеме реализованной продукции: 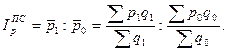
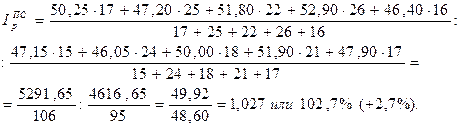
Вывод: повышение средней цены реализации единицы продукции в отчетном периоде по сравнению с базисным на 2,7% достигнуто за счет изменения, как самих цен, так и в результате изменения структуры реализованной продукции.
Для того чтобы устранить влияние изменения структуры продукции на динамику средней цены реализации, определим для двух рассматриваемых периодов изменения средней цены реализации при той же структуре продукции в текущем периоде. Для этого определим индекс цен фиксированного (постоянного) состава:
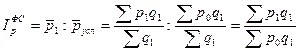 .
.
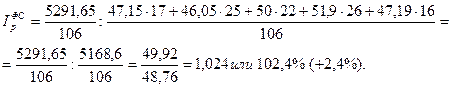
Вывод: повышение средней цены реализации единицы продукции в текущем периоде по сравнению с базисным за счет только повышения цен на продукцию составляет 2,4%.
С целью сравнения влияния изменения цены по отдельным предприятиям на среднюю цену реализации продукции и определения степени влияния изменения структуры реализованной продукции, определим индекс структурных сдвигов:
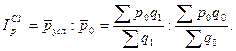
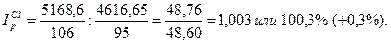
Проверка: 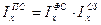 ;
; 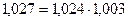 .
.
2. Сравнение уровней средних цен по абсолютным значениям показывает:
а) общий прирост средней цены составляет 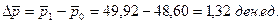
б) прирост цены за счет изменения самих цен 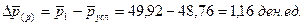
в) прирост цены в результате структурных сдвигов 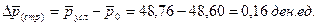
Вывод: общий прирост средней цены реализации единицы продукции на 1,32 ден.ед. является результатом роста цен на отдельных предприятиях на 1,16 ден.ед. и улучшением структуры реализованной продукции на 0,16 ден.ед.
3. В расчете на всю продукцию текущего периода абсолютный рост стоимости реализованной продукции в результате роста средней цены на 1,32 ден.ед. будет составлять: 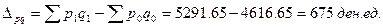 , в т.ч. в результате изменения цен по отдельным предприятиям
, в т.ч. в результате изменения цен по отдельным предприятиям 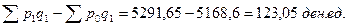 и благодаря улучшению структуры реализованной продукции на 551,95 ден.ед. (
и благодаря улучшению структуры реализованной продукции на 551,95 ден.ед. ( 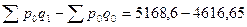 ).
).
Дата добавления: 2015-02-25; просмотров: 2149;
