Средневзвешенные индексы
Агрегатный способ представления общих индексов в статистике является наиболее распространенным. Вместе с тем используется и другой подход расчета общих индексов как средних из соответствующих индивидуальных индексов, или средневзвешенных индексов.
К расчету средневзвешенных индексов обращаются в тех случаях, когда первичная (исходная) информация не позволяет рассчитать общий агрегатный индекс. Существует две формы средневзвешенных индексов: среднеарифметическая и среднегармоническая. Как правило, средний арифметический индекс применяется при индексации количественных показателей (например, физического объема продукции), а средний гармонический – при индексации качественных показателей (например, цен).
При расчете среднего арифметического индекса индексируемая величина числителя выражается через индивидуальный индекс.
Например, необходимо вычислить общий индекс физического объема продукции Iq , когда по исходным данным известны индивидуальные индексы физического объема (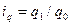 
) и стоимость продукции каждого вида за базисный период ( 
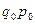). Тогда общий индекс физического объема продукции можно определить как среднюю арифметическую взвешенную из индивидуальных индексов. Для этого заменяем неизвестное количество продукции отчетного периода ( 
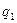) произведением 
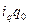. Тогда общий индекс физического объема продукции приобретет вид: 
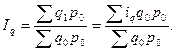(8.14)
Эта формула представляет собой среднюю арифметическую из индивидуальных индексов физического объема продукции, взвешенную по стоимости продукции базисного периода.
Если индексируемая величина выражается через индивидуальный индекс в знаменателе, то индекс имеет название среднего гармонического индекса.
Например, известны индивидуальные индексы цен (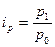 
) и стоимость каждого вида продукции за текущий (отчетный) период ( 
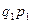), но неизвестны данные о цене единицы продукции за базисный период ( 
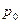). Чтобы найти средний гармонический индекс цен, цену базисного периода ( 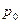) заменяем тождественным ей соотношением 
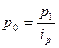. Вследствие этого индекс цен будет иметь вид: 
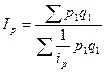(8.15)
Эта формула представляет собой среднюю гармоническую из индивидуальных индексов цен, взвешенную по объему продукции текущего периода.
Пример. Имеются следующие данные:
| Вид изделия | Произведено в отчетном периоде, тыс. шт. q | Затраты на 1 изд, чел./час | |
| в отчетном периоде t1 | в базисном периоде t0 | ||
| А | 2,3 | ||
| Б | 1,5 | 1,8 | |
| В | 0,5 | 0,55 |
Индивидуальные индексы производительности труда (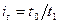 
) составят: по изд.А 
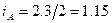; по изд.Б 
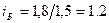; по изд.В 
;
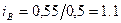Общий индекс производительности труда в агрегатной форме составит:
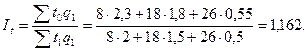
Общий индекс производительности труда как средний из индивидуальных индексов составит:
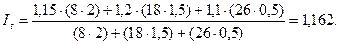
Дата добавления: 2015-02-25; просмотров: 4216;