Признак сходимости Даламбера
Дан ряд с положительными членами 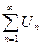 и
и 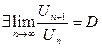
Если 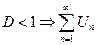 - сходиться
- сходиться
Если 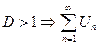 - расходиться
- расходиться
Если 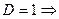 - вопрос о сходимости не решен.
- вопрос о сходимости не решен.
Доказательство:
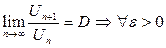
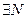 , начиная с которого
, начиная с которого
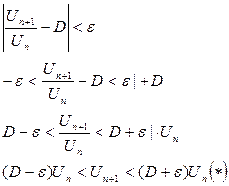
1) Пусть D<1 выберем 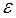 настолько малым, чтобы
настолько малым, чтобы 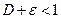
обозначим 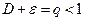
рассмотрим правую часть 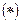
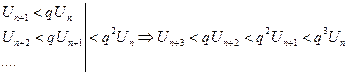
Рассмотрим ряд из членов геометрической прогрессии 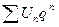 , т.к. ряд q<1
, т.к. ряд q<1  этот ряд сходится.
этот ряд сходится.
Т.к. исходный ряд меньше сходящегося ряда из членов меньшего ряда, то исходный ряд сходится по I признаку сравнения.
2) Пусть D>1 выберем 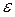 настолько малым, чтобы
настолько малым, чтобы 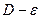 >1
>1 
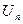 <(D-
<(D- 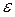 )
) 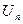
из левой части 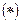

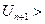
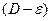
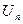 >
> 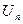
следовательно, члены ряда растут 
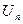 не стремится к 0
не стремится к 0 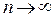 , ряд расходится по достаточному признаку расходимости.
, ряд расходится по достаточному признаку расходимости.
3) D=1
Возьмем 2 обобщенно гармонических ряда 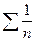 – расходится и
– расходится и 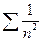 - сходится.
- сходится.
Для 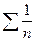 D=
D= 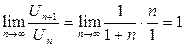
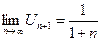
Для 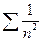 D=
D= 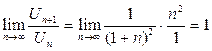
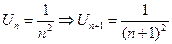
При D=1 ряд может сходиться или расходиться и вопрос о сходимости ряда остается открытым.
Конец доказательства.
Примеры:
1) 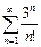
2) 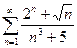
3) 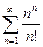
Дата добавления: 2015-01-09; просмотров: 1050;
