Разложение многочлена в комплексной области на линейные множители.

Пусть P_n (z) – многочлен степени n, а z₁ – его корень. Тогда по теореме Безу P_n (z) можно представить в виде:

P_n (z) = (z – z₁) Q_n-1 (z),

где Q_n-1 – многочлен степени n – 1. Если при этом Q_n-1 (z₁) = 0, его вновь можно представить как ( z – z₁ )Q_n-2 (z), a P_n (z) = (z – z₁)Q_n-2 (z).

Определение 8.3. Натуральное число k₁ называется кратностью корня z₁ многочлена P_n (z), если этот многочлен делится на 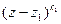, но не делится на . Корень кратности 1 называется простым,а корень кратности, большей 1, - кратным.

Итак, если z₁ – корень P_n кратности k₁ , то 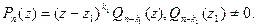Из основной теоремы алгебры следует, что многочлен 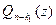тоже имеет корень. Обозначим его z₂ , а его кратность k₂ . Тогд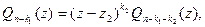а а 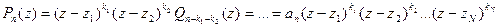, (8.2)

где 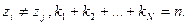Следовательно, в комплексной области всякий многочлен можно разложить на линейные множители.