Формула интегрирования по частям.

Теорема 6.3. Если функции u(x) и v(x) дифференцируемы на некотором промежутке, и на нем существует интеграл 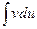, то на нем существует и интеграл 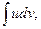причем

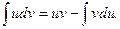(6.3)

Доказательство.

d(uv) = vdu + udv, поэтому udv = d(uv) – vdu. Проинтегрируем обе части полученного равенства, учитывая, что Тогда что и требовалось доказать. Существование интеграла в левой части равенства следует из существования обоих интегралов в правой части.

Пример.