Замена переменной в неопределенном интеграле.

Теорема 6.2. Пусть функция f(x) определена на множестве Х, а функция φ(t) – на множестве Φ, причем 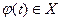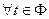. Тогда, если функция f(x) имеет первообразную F(x) на Х, а φ(t) дифференцируема на Φ, то

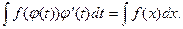(6.1)

Доказательство.

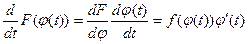, поэтому функция F(φ(t)) является первообразной функции f(φ(t)) φ΄(t). Следовательно, 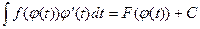. С другой стороны, при x = φ(t) 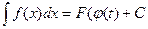. В полученных формулах равны правые части, следовательно, равны и левые, что доказывает справедливость формулы (6.1).

Замечание 1. Формулу (6.1) называют формулой интегрирования подстановкой.

Замечание 2. Часто удобно бывает использовать формулу (6.1) «в обратную сторону»:

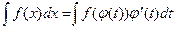, (6.2)

то есть заменять переменную х функцией новой переменной t. Формула (6.2) носит название формулы интегрирования заменой переменной.

Замечание. Формулы (6.1) и (6.2) показывают, что вид первообразной не изменяется при замене независимой переменной х на функцию φ(t), поэтому их называют формулами инвариантности интегрирования.

Примеры.

1. 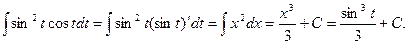При этом была сделана подстановка x = sin t.

2.

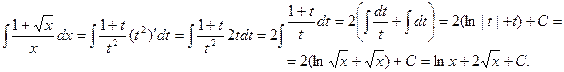
Интеграл был вычислен с помощью замены переменной: x = t².