Первообразная. Неопределенный интеграл и его свойства. Табличные интегралы. Замена переменной и интегрирование по частям в неопределенном интеграле.
Определение 6.1. Функция F(x) называется первообразной (для) функции f(x) на некотором множестве значений х, если F΄(x) = f(x) на этом множестве.
Теорема 6.1. Если функции F(x) и G(x) являются первообразными одной и той же функции f(x) на некотором множестве, то необходимым и достаточным условием этого является то, что G(x) = F(x) + C, где С – любая постоянная.
Доказательство.
- Пусть F(x) - первообразная f(x), то есть F΄(x) = f(x). Тогда для любого числа C (F(x) + C)΄= F΄(x) + C΄= F΄(x) + 0 = f(x), то есть F(x) + C - первообразная f(x).
- Пусть F(x) и G(x) – две различные первообразные одной и той же функции f(x). Тогда (F(x) – G(x))΄= F΄(x) - G΄(x) = f(x) – f(x) = 0, следовательно, F(x) – G(x) = C (по следствию из теоремы Лагранжа). Теорема доказана.
Таким образом, если функция на данном множестве имеет одну первообразную, то она имеет их бесконечно много, причем все они отличаются друг от друга постоянными слагаемыми.
Определение 5.2. Совокупность всех первообразных функции f(x) на некотором множестве называется ее неопределенным интегралом.
Обозначение: 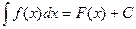 .
.
f(x) при этом называется подынтегральной функцией, а f(x)dx – подынтегральным выражением.
Свойства неопределенного интеграла.
1. 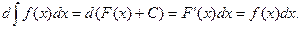
2. 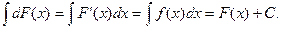
3. 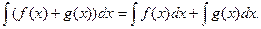 Действительно,
Действительно, 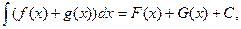 а
а 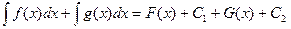 . Но, поскольку С1+С2 – произвольная постоянная, выражения в левой и правой частях равны.
. Но, поскольку С1+С2 – произвольная постоянная, выражения в левой и правой частях равны.
4. 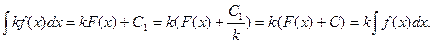
Замечание. Все перечисленные свойства формулировались и доказывались в предположении, что на некотором множестве существуют первообразные функций f(x) и g(x), равные соответственно F(x) и G(x).
Табличные интегралы.
Из определения первообразной и неопределенного интеграла следует, что таблицу основных интегралов можно получить из таблицы основных производных (см. лекцию 18 первой части курса), считая производные табличных функций подынтегральными функциями, а сами функции – их первообразными.
1. 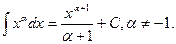 2.
2. 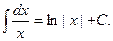
3. 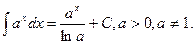 3΄)
3΄) 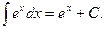
4. 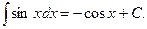 5.
5. 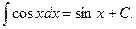
6. 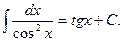 7.
7. 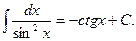
8. 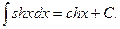 9.
9. 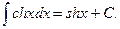
10. 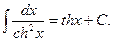 11.
11. 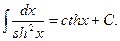
12. 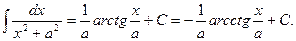
13. 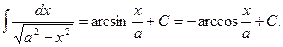
Можно добавить к этой таблице еще несколько формул, не следующих непосредственно из таблицы производных, но удобных для вычисления многих интегралов, а именно:
14. 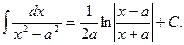 15.
15. 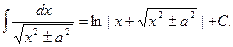
Доказательство справедливости этих формул предлагается провести самостоятельно.
Примеры.
1. 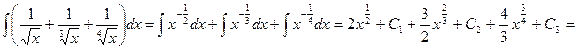
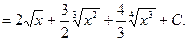
2. 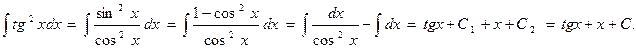
Дата добавления: 2015-03-19; просмотров: 2229;
