Несобственные интегралы 2-го рода).

Определение 15.3. Пусть функция f(x) определена и непрерывна при a ≤ x < b и имеет разрыв при x = b. Тогда 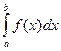определяется следующим образом:

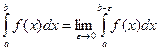(15.5)

и называется несобственным интегралом 2-го рода. Если предел, стоящий справа, существует и конечен, интеграл называется сходящимся, в противном случае – расходящимся.

Аналогичным образом определяются несобственные интегралы от функции, имеющей разрыв при х = а: 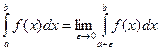и от функции, разрывной в точке с (a<c< b):

,

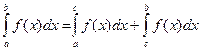если существуют оба интеграла, стоящие в правой части равенства.

Для несобственных интегралов 2-го рода справедливы те же утверждения, что и для несобственных интегралов 1-го рода:

Теорема 15.3(признак сравнения). Пусть функции f(x) и φ(х) непрерывны при 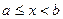и имеют разрыв при x = b. Пусть, кроме того, 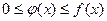при . Тогда:

1) если интеграл 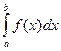сходится, то сходится и интеграл ;

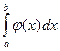2) если интеграл 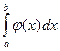расходится, то расходится и интеграл .

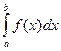Теорема 15.4. Если f(x) – знакопеременная функция, непрерывная на [a,b) и имеющая разрыв при x =b, и если 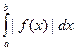сходится, то сходится и интеграл .

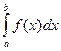Замечание 1. Эти теоремы доказываются так же, как теоремы 15.1 и 15.2.

Замечание 2. При выполнении условий теоремы 15.4 несобственный интеграл 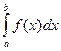называется абсолютно сходящимся, а функция f(x) – абсолютно интегрируемой.

Следствие из теоремы 15.3.

Если при 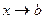, то при α < 1 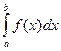сходится, а при α ≥ 1 расходится.

Доказательство.

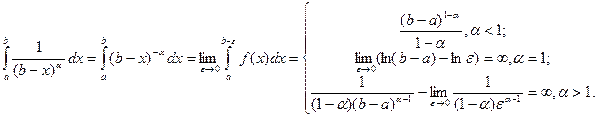
Таким образом, интеграл 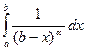сходится при α < 1 и расходится при α ≥ 1.