Динамические переменные и интегралы движения.

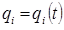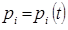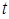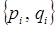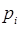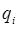В гамильтоновой механике задание координат и импульсов в каждый момент времени однозначно характеризует состояние системы. По этой причине переменные – основные динамические величины механической системы. Наряду с ними возникает необходимость в использовании различных функций от и , отражающих детали динамики системы. В общем случае динамическая величина 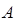– это некоторая функция обобщённых координат 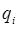и импульсов 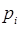, а также времени :

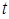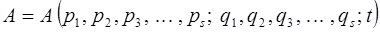
или сокращённо:

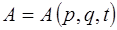
Динамические величины имеют неформальный смысл лишь на траектории движения. Чтобы понять зависимость динамической величины 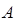от времени 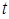, исследуем её полную производную по времени 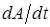. Итак, пускай у нас имеется некоторая динамическая переменная 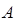, описывающая систему с s степенями свободы, при этом:

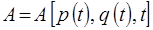
Очевидно:

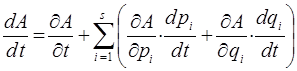
или

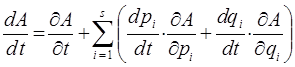
учитывая, что на траектории движения в механике выполняется:

имеем соответственно:

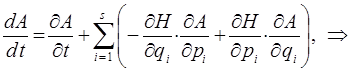
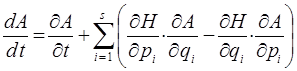
При выводе данного уравнения, автоматически появилась характерная конструкция, называемая скобкой Пуассона. В общем случае, для двух динамических переменных A и B, её обозначают через 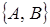и определяют выражением вида:

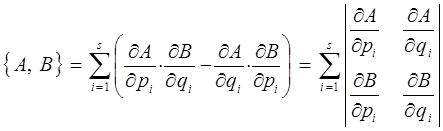
тогда с учётом того, что:

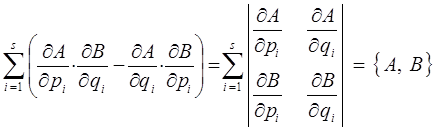
выражение вида:

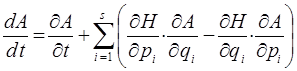
может быть переписано и представлено к виду:

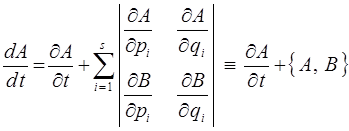
Следовательно, имеет место общая механическая формула:

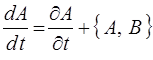
позволяющая записать выражение:

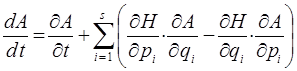
в более компактной форме, используя скобки Пуассона. Последние, в свою очередь, обладают следующими основными свойствами:

1. Если динамические переменные A и B в скобке Пуассона поменять местами, то скобка изменит свой знак на противоположный (антисимметричность скобок):

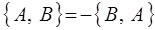
и как следствие:

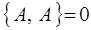
2. Если одна из динамических величин (переменных) в скобках Пуассона является величиной постоянной (например, переменная C), то соответствующая скобка будет также равна нулю, что аналогично правилам дифференцирования:

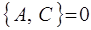
и аналогично:

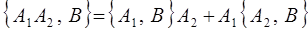
отождествляя 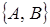с операцией дифференцирования по B:

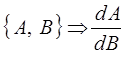
получаем, что:

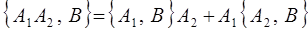
формально эквивалентно операции:

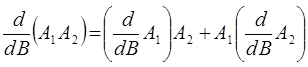
3. Если одна из динамических переменных в скобке Пуассона представляется суммой двух динамических переменных, например:

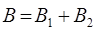
то вследствие линейности скобок Пуассона оказывается справедливым:

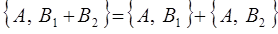
4. Между скобками Пуассона, полученными циклической перестановкой трёх динамических переменных A, B и C, существует соотношение:

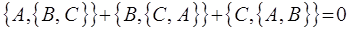
называемое также тождеством Якоби.

5. В качестве динамических переменных в общем случае могут выступать разные величины. Так, если в качестве последних выступают обобщённые координаты 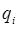и импульсы 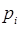, то построенные на их основе скобки Пуассона, будут равны:

и соответственно:

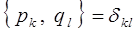
где 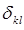– символ Кронекера. По определению:

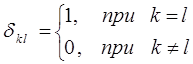
Для того чтобы убедиться в справедливости наших рассуждений. Найдём 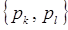, где 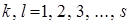. Учитывая, что импульсы явно не зависят от обобщённых координат и для всех i, k:

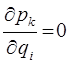
Кроме того, очевидно, что:

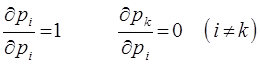
Последний факт записываем с помощью так называемого δ-символа Кронекера:

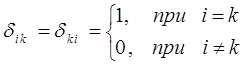
т.е. 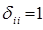, а в остальных случаях – нулю. Это в свою очередь означает, что вместо:

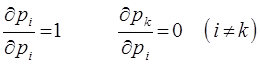
необходимо писать:

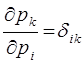
В расчётах необходимо иметь ввиду следующее свойство сумм с δ-символом:

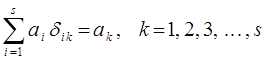
Иными словами, из всей суммы по i, δ-символ вырезает лишь одно значение – 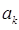, когда в процессе суммирования текущий индекс i достигнет значения внешнего индекса k. Учитывая, что:

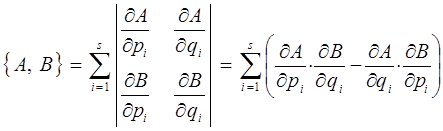
имеем:

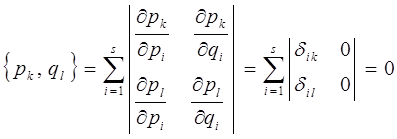
аналогично проверяется:

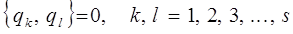
при этом необходимо отметить, что скобка Пуассона, включающая в себя координату и импульс, не всегда равна нулю.

Действительно, имеем:

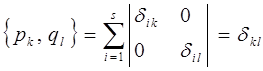
где учтено:

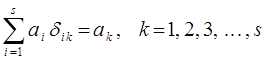
и таким образом, для канонически сопряжённых величин имеем:

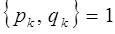
Если в качестве динамической переменной выступает функция Гамильтона H, то для консервативной системы из выражения:

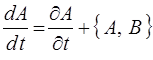
следует, что:

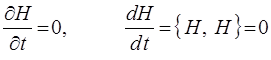
Это в свою очередь означает, что функция Гамильтона H является величиной постоянной. Уравнения Гамильтона, записанные через скобки Пуассона, приобретают симметричный вид:

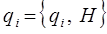
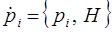
Скобки Пуассона не упрощают решения уравнений движения, однако оказалось, что именно они приводят к математическому аппарату, который используется для формулировки основных теоретических положений квантовой механики. Введенные нами выше понятия динамической переменной неразрывно связаны с таким понятием как интеграл движения. По определению динамическая величина А есть интеграл движения, если А сохраняется на протяжении всей траектории движения. Это в свою очередь означает, что такая величина не зависит от времени и оказывается справедливым механическое уравнение:

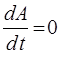
Поскольку во многих случаях А явно от времени не зависит:

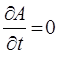
тогда уравнение:

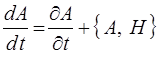
при условии, что:

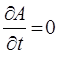
может быть сведено к виду:

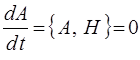
Это в свою очередь означает, что величину А можно рассматривать в качестве интеграла движения только при условии исчезновения скобки Пуассона 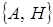величины А и гамильтониана H. Для случая консервативных систем уравнение:

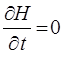
может быть представлено к виду:

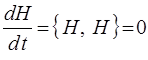
что полностью воспроизводит закон сохранения энергии.