Интегралы от неограниченных функций

Если функция f(x) непрерывна при a ≤ x < c и c < x ≤ b, а в точке c тер­пит бесконечный разрыв, то несобственный интеграл от этой функции опреде­ляется формулой

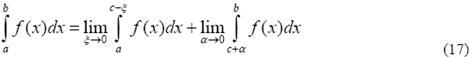
В случаях c = b или a = c, то

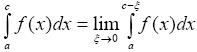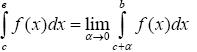или (18)

Несобственные интегралы (17)−(18) называются сходящимися, если пределы конечны; в противном случае их называют расходящимися.

П р и м е р. Вычислить несобственный интеграл 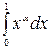(α< 0).

Решение. Функция x^α при α ≥ 0 на отрезке [0, 1] непрерывна и интеграл является собственным. При α < 0 функция x^α терпит в точке 0 бесконечный разрыв.

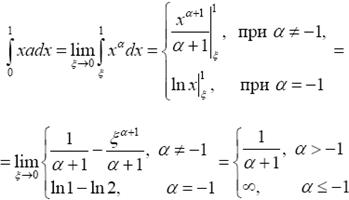
Интеграл сходится при α > −1.