Геометрические приложения определенного интеграла
1. Вычисление площади плоской фигуры
1.1. Пусть функция f (x) непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции y = f (x), может быть вычислена по формуле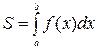 
.
1.2. Если f2(x) > f1(x)на отрезке [a, b], f1(x), f2(x) − непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций y = f1(x), y = f2(x) вычисляется по формуле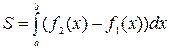 
(рис. 10).
1.3. Если функция f (x) на отрезке [a, b] принимает значения разных знаков, то площадь фигуры, заключенная между кривой y = f (x) и осью OX , равна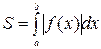 
(рис. 11).
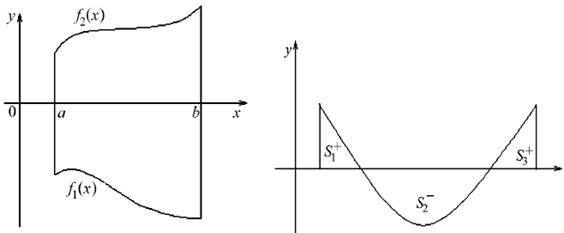
Рис. 10 Рис. 11
П р и м е р. Вычислить площадь фигуры, ограниченной графиками функций y(x) = x и y(x) = 2 − x2 .
Решение. Вычислим координаты точек пересечения графиков этих функций. Для этого решим систему
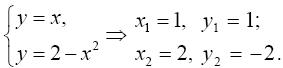
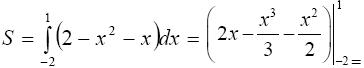
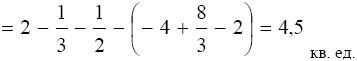
Дата добавления: 2015-01-24; просмотров: 1321;