Изгиб за пределами упругости.

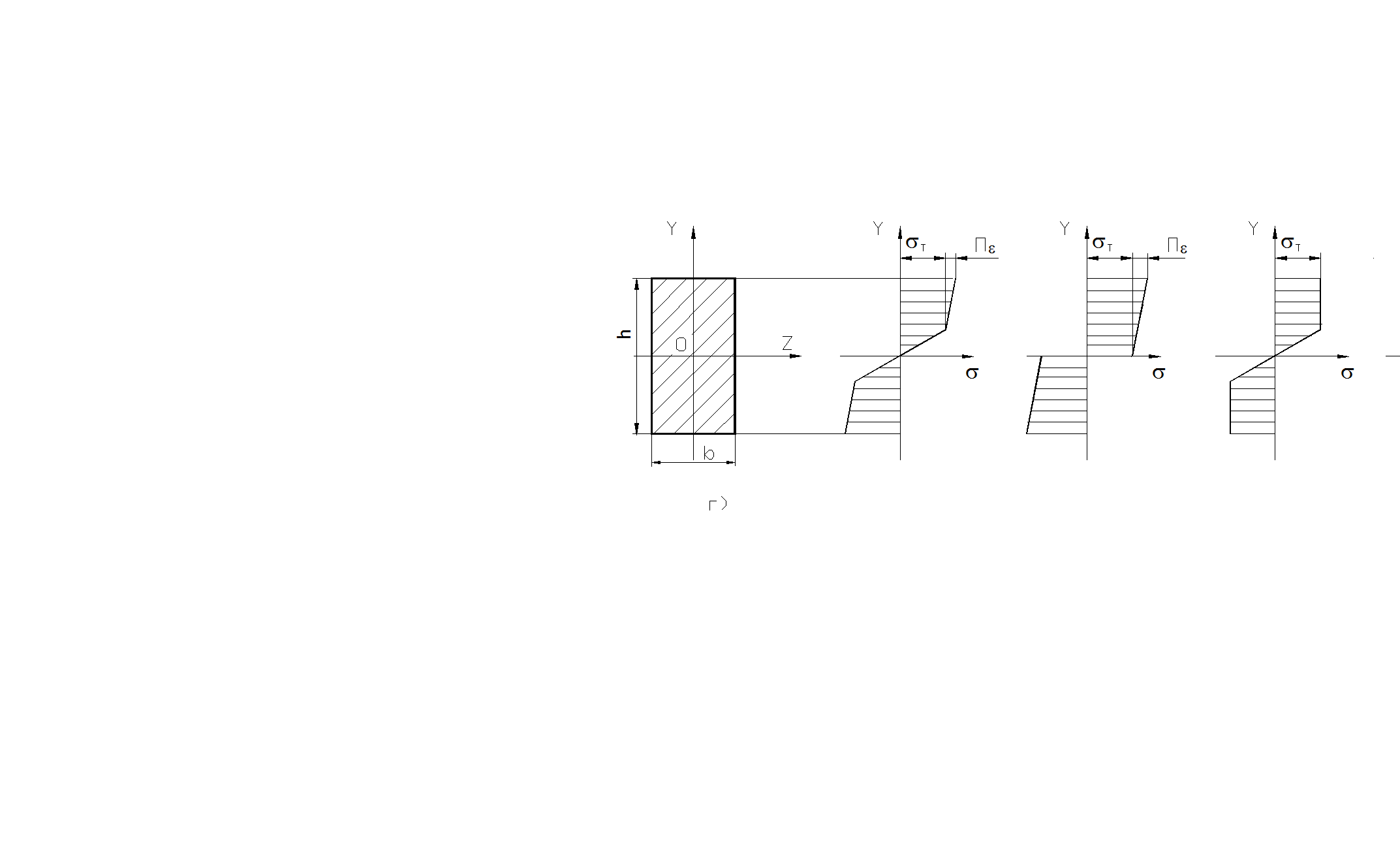
При технологической операции гибке различают: линейный упругопластический изгиб с упрочнением (рис.2.30,а); линейный чистопластический изгиб с упрочнением (рис.2.30,б); линейный упругопластический изгиб без упрочнения (рис.2.30,в); чистопластический изгиб без упрочнения (рис. 2.30,г); объемный пластический изгиб (рис.2.30,д).

Есть несколько гипотез. Одна из них предложена Губером и Мизесом- пластическое состояние тела наступает тогда, когда интенсивность напряженности равна

s_i= k,

где k – некоторое значение интенсивности напряжений для каждого материала.

Согласно этому условию для касательных напряжений должно быть

t_т= s_т /3^0,5= k.

Напряженное состояние при чистом объемном изгибе (без поперечных сил) широкого бруса характеризуется тремя главными нормальными напряжениями: s_z- в аксиальном направлении (ось гиба); s_q- в тангенциальном направлении; s_r- в радиальном направлении.(рис.2.30,д).

Исследования, выполненные в ЦНИИТМАШе, показали, что в процессе гибки происходит изменение геометрии детали в зоне гиба (рис. 2.30,д), нейтральная ось смещается, стенка трубы по наружнему радиусу утоняется, а по внутреннему- становится толще и т.д. Однако в самом простом случае изгибающий момент можно рассчитать с помощью выражения

М_и= 1,5W_zs_т,

где W_z - геометрический момент сопротивления сечения.

а) б) в) г)

сечение балки

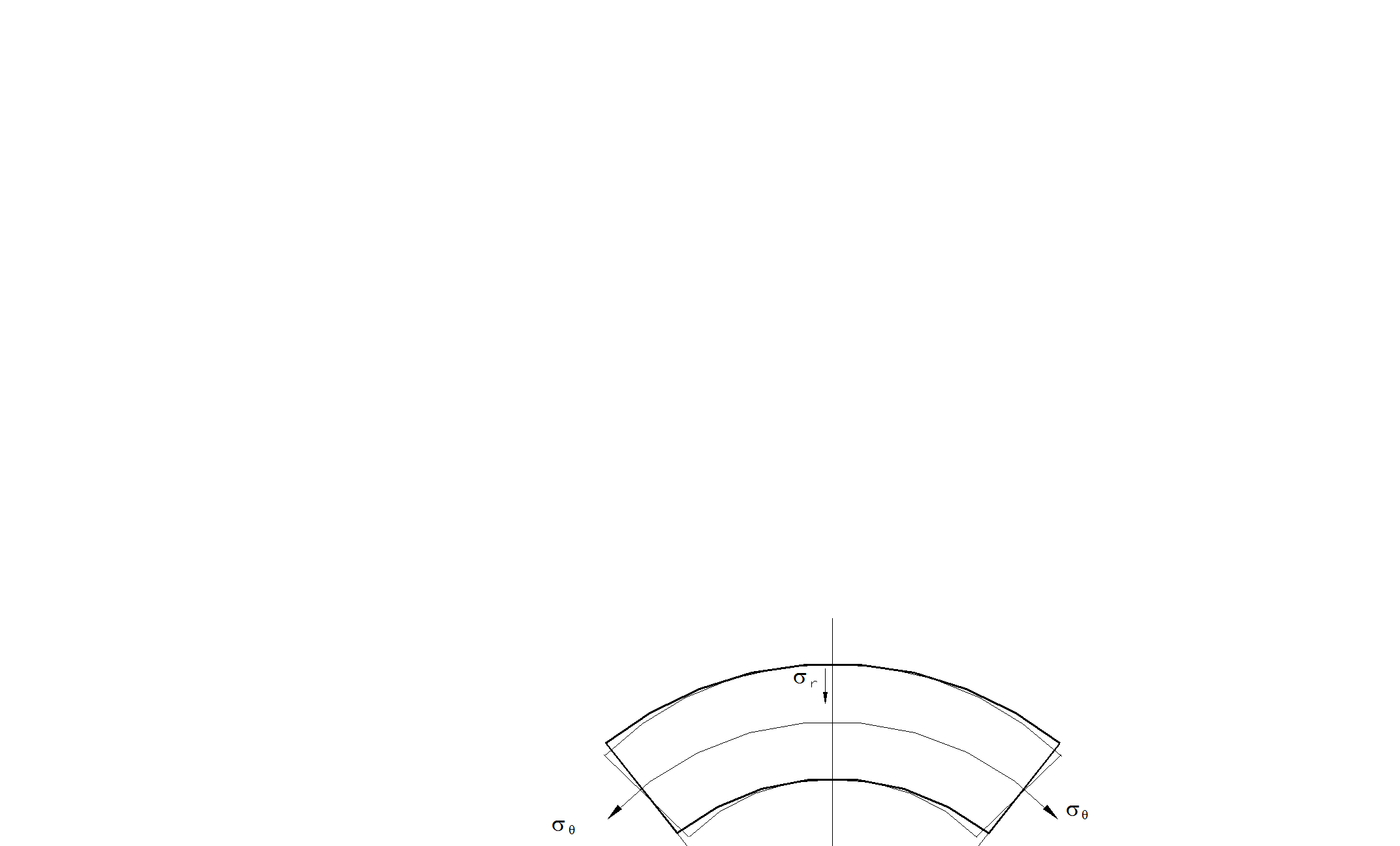
д)

Рис.2.30. Изгиб за пределами упругости (П= (2…10)10³МПа – модуль упрочнения).

При чистопластическом изгибе остаточные напряжения в крайних слоях зависят только от профиля сечения (для прямоугольника из стали- s_ост @ 0,5s_т; для круга- s_ост @ 0,7s_т).

Широко применяется многократный пластический изгиб, который может быть многократным последовательным (без изменения знака), многократным знакопеременным, как прямого, так и изогнутого брусов.

Промежуточные разгрузки при многократном последовательном изгибе не влияют на величину изгибающего момента, которая определяется радиусом гиба.

При многократных знакопеременных изгибах на малую кривизну выравниваются механические свойства материала, получившиеся от распрямления первоначальной кривизны.