Расчет статически неопределимых стержневых систем.

В ряде инженерных задач внутренние силы в стержнях не могут быть определены с помощью одних уравнений статики из-за того, что число неизвестных сил в таких конструкциях больше чем число уравнений равновесия. Такие задачи называются статически неопределимыми.

Если элементы конструкции работают в основном на сжатие или растяжение, то такая стержневая система называется фермой. Ферма состоит из прямых стержней, образующих треугольники.

Если элементы стержневой системы работают в основном на изгиб или кручение, то система называется рамой.

Существуют плоские и пространственные системы.

Разность между числом неизвестных (реакций опор и внутренних сил) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы, носит название степени или числа статической неопределимости. Существуют системы один, два ... n раз статически неопределимы.

Положение жесткого бруса в пространстве определяется 6-ю независимыми координатами, т.е. брус обладает 6-ю степенями свободы. На брус могут быть наложены ограничения (связи), обусловливающие его определенное положение в пространстве. При 6 связях брус превращается в жесткую неизменяемую систему. Число дополнительных связей равно степени статической неопределимости системы.

Так, заделка в плоскости дает 3 связи (ограничения в перемещениях по x, y, по углу поворота); шарнир в плоскости- 2 связи (ограничения по перемещениям).

Рассмотрим наиболее широко применяемый в машиностроении метод раскрытия статической неопределимости стержневых и рамных систем- метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами, величина которых подбирается так, чтобы перемещения соответствовали ограничениям, накладываемым отброшенными связями. При указанном способе решения неизвестными оказываются силы. Существуют и другие методы.

Раскрытие статической неопределимости методом сил начинается с отбрасывания дополнительных связей. Такая система становится статически определимой и носит название основной системы. Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем.

После отбрасывания дополнительных связей вводят неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения вводят силы. Там, где запрещены угловые смещения вводят моменты. Силовые факторы обычно обозначают символом X_i, где i - номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Для внутренних связей силы X_i являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются и к левой и к правой частям системы.

Для определения сил составляют канонические уравнения.

Здесь взаимное смещение точек системы обозначают буквой d_ik, где первый индекс соответствует напряжению перемещения, а второй - силе.

Так, запись d_{1[X1, X2,...P]}= 0, означает, что при действии силы X₁ перемещение определяется суммой всех сил, как заданных, так и неизвестных.

Аналогично можно записать для перемещения в направлении силы X₂-

d_{2[X1, X2,...P]}= 0 и т.д.

Поскольку перемещения должны быть равными нулю, то при действии всех сил будет

d_{1[X1, X2,...P]}= d_1X1+ d_1X2+...+ d_1Р= 0.

. . .

d_{n[X1, X2,...P]}= d_nX1+ d_nX2+...+ d_nР= 0. (2-156)

Так как каждое перемещение пропорционально соответствующей силе, то d_iXk= d_ik X_k.

C учетом этого система (2-156) может быть переписана в форме

d₁₁ Х₁+ d₁₂ Х₂+...+d_1n Х_n+ d_1Р= 0

d₂₁ Х₁+ d₂₂ Х₂+...+d_2n Х_n+ d_2Р= 0

. . .

d_n1 Х₁+ d_n2 Х₂+...+d_nn Х_n+ d_nР= 0. (2-157)

Эти уравнения являются каноническими уравнениями метода сил. Число их n-это степень статической неопределимости системы.

Если обратиться к интегралам Мора, то для определения перемещения d_ik, надо вместо внешних сил рассматривать единичную силу, заменяющую k- й фактор. Поэтому внутренние моменты и силы из выражения (2-153) заменим на M_кk, M_xk, M_yk, N_k, Q_xk, Q_yk, понимая под ними внутренние моменты и силы от единичного k-го фактора. В итоге получим

d_ik = 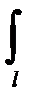M_{к k} М_кi(GJ_к)^-1dz+ 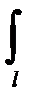M_{х k} М_хi(EJ_x)^-1dz+ 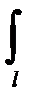M_{y k} М_yi(EJ_y)^-1dz

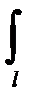+ N_P N₁(Ef)^-1dz+ 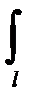k_xQ_xP Q_x1(E f)]dz+ 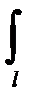[k_yQ_yP Q_y1(G f)^-1dz, (2-158)

где M_кi, M_xi ....- внутренние моменты и силы, возникающие под действием i-го единичного фактора. Таким образом, коэффициенты d_ik получаются как результат перемножения i- го и k- го внутренних единичных силовых факторов. Индексы i и k непосредственно указывают, какие факторы должны быть перемножены под знаком интегралов Мора. Если рама состоит из прямых участков и можно пользоваться правилом Верещагина, то d_ik представляют собой результат перемножения i-х единичных эпюр на k-е единичные эпюры. При этом d_ik= d_ki .

Раскрыть статическую неопределимость можно также с помощью метода сравнения деформаций.

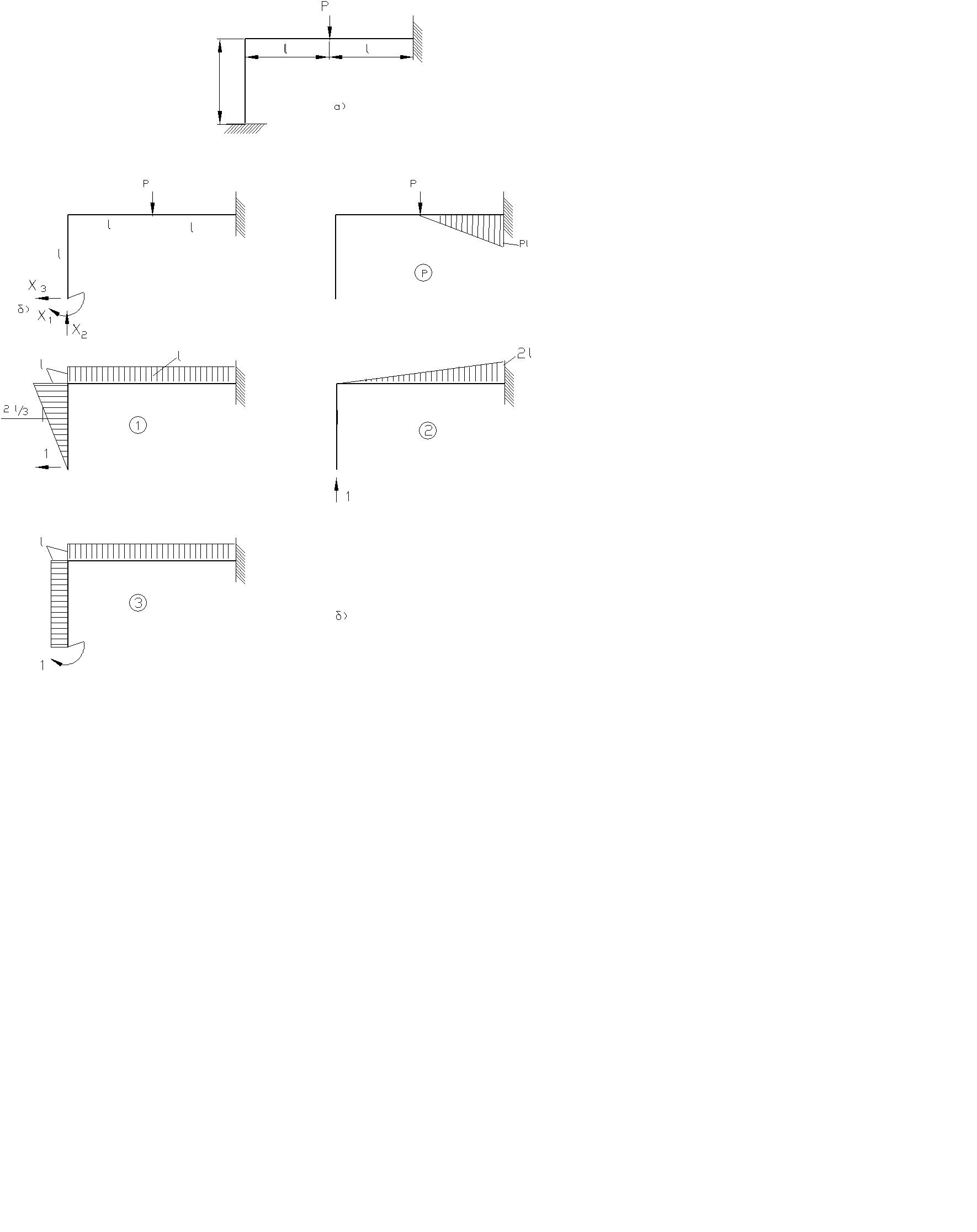
Пример 2.9: Раскрыть статическую неопределимость системы, изображенную на рис. 2.35,а

Здесь длина каждого плеча равна l.

Так как деформации из-за изгиба и кручения значительно превышают деформации от растяжения и сдвига, то последними 3-мя интегралами в выражении (2-158) пренебрежем.

Запишем уравнения статики для сил по вертикальной оси Y и горизонтальной оси Z и изгибающих моментов

åY=0; åZ= 0; åМ= 0.

Поскольку заделка дает 3 связи (ограничения), то две заделки дают 6 связей. Следовательно, в этом случае имеем степень статической неопределимости n= 6-3= 3.

Выбирая основную систему, отбрасываем левую заделку. Действие ее заменяем двумя силами X₁, X₂ и моментом X₃ (рис.2.32,б).

Канонические уравнения (2-157) для рассматриваемой системы принимают вид

d₁₁ Х₁+ d₁₂ Х₂+ d₁₃ Х₃ = - d_1Р ,

d₂₁ Х₁+ d₂₂ Х₂+ d₂₃ Х₃ = - d_2Р ,

d₃₁ Х₁+ d₃₂ Х₂.+d₃₃ Х₃ = - d_3Р .

Определяем коэффициенты уравнений, полагая, что жесткость всех участков рамы постоянна и равна EJ.

Величина d₁₁ определяется перемножением первой единичной эпюры самой на себя. Для каждого участка берется, следовательно, площадь эпюры и умножается на ординату этой же эпюры, проходящую через ее центр тяжести

d₁₁= (EJ)^-1[(l²/2)(2l/3)+ 2l²l]= 7l³/(3EJ).

Здесь d₁₁ при l= k всегда положительны, т.к. площади эпюр и ординаты имеют общий знак.

Определяем далее, и остальные коэффициенты уравнений, перемножая соответствующие эпюры

d₁₂= d₂₁= 2l³/(EJ); d₁₃= d₃₁= 5l²/(2EJ); d₂₂= 8l³ /(3EJ); d₂₃= d₃₂= 2l²/(EJ); d₃₃= 3l/(EJ); d_1P=- Pl³ /(2EJ); d_2P=- 5Pl³ /(6EJ); d_3P=- Pl² /(2EJ).

Подставляем найденные коэффициенты в канонические уравнения. После сокращений получим

(7/3)lX₁+ 2lX₂+ (5/2)X₃= Pl/2;

2lX₁+ (8/3)lX₂+ 2X₃= 5Pl/6;

(5/2)lX₁+ 2lX₂+ 3X₃= Pl/2.

Рис.2.35 К примеру 2.9

Решая эти уравнения, находим

X₁= -P/4; X₂= 7P/16; X₃= Pl/12.

На этом раскрытие статической неопределимости заканчивается.

Пример 2.10: Определить вертикальное перемещение точки В стержневой системы на рис. 2.36.

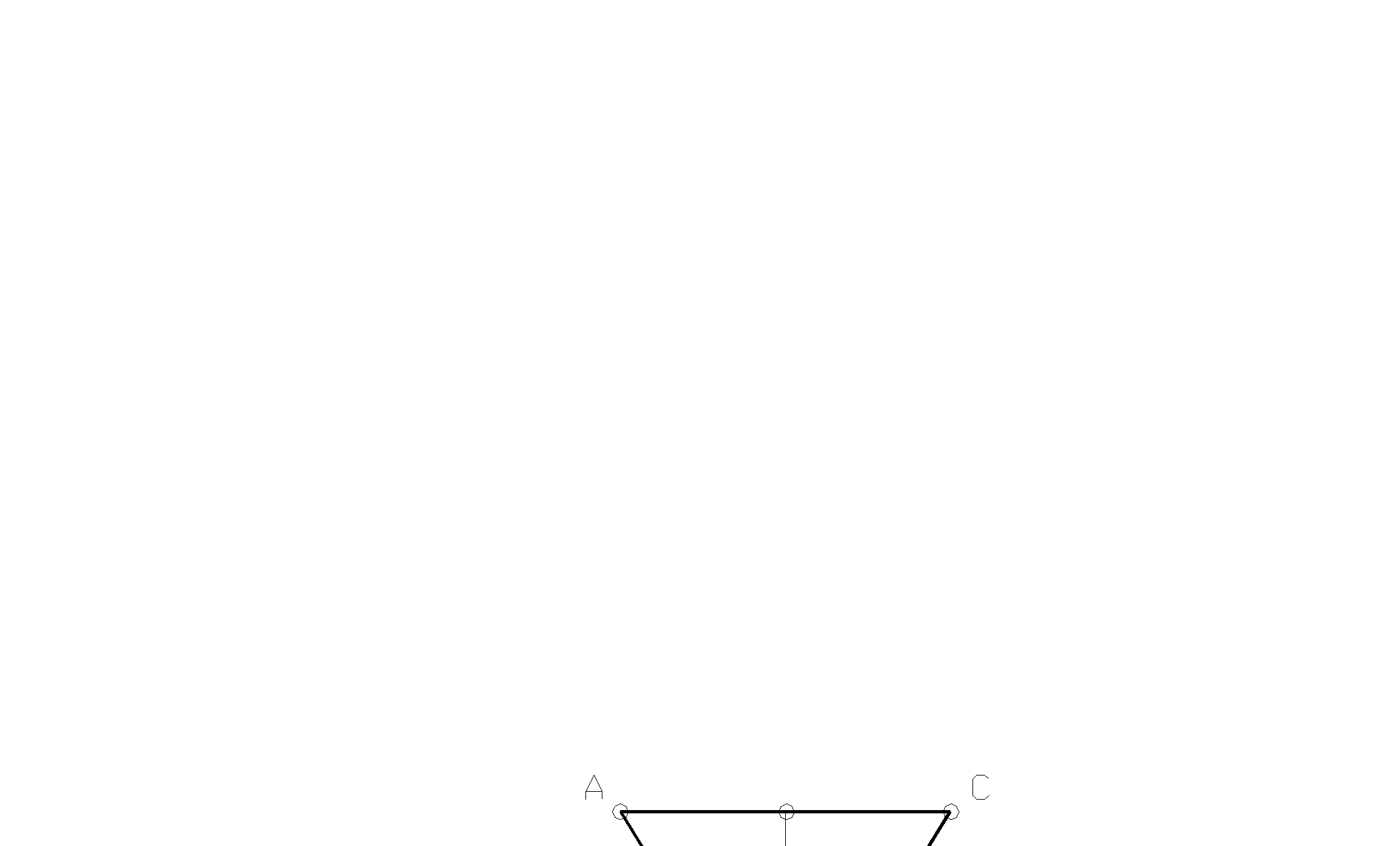
Рис. 2.36

К примеру 2.10

Здесь АВ= ВС, а в точках А, В, С установлены шарниры. По стержню АВ направлена сила N₁, а по ВС- N₂.

Так как F= N₁cosa + N₂cosa= =2N₁cos a, то N₁= F/(2cosa).

Потенциальная энергия деформации стержней

U= 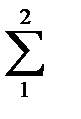N_i ²l_i /(2Ef)= [l/(2fE)](N₁²+ N ²₂)= N ²₁l/(fE)= F ²l/(4fEcos²a).

Используя теорему Кастильяно, для перемещения от силы F получим d_В =¶U/¶F= F l/(2fEcos²a).

Пример 2.11: Определить вертикальное перемещение точки В стержневой системы на рис. 2.37.

Здесь АВ= ВС= l₁; DB= l₂. В точках А, В, С, D установлены шарниры. По стержню АВ направлена сила N₁, по DB- N₂, по ВС- N₃.

Очевидно N₁= N₃.

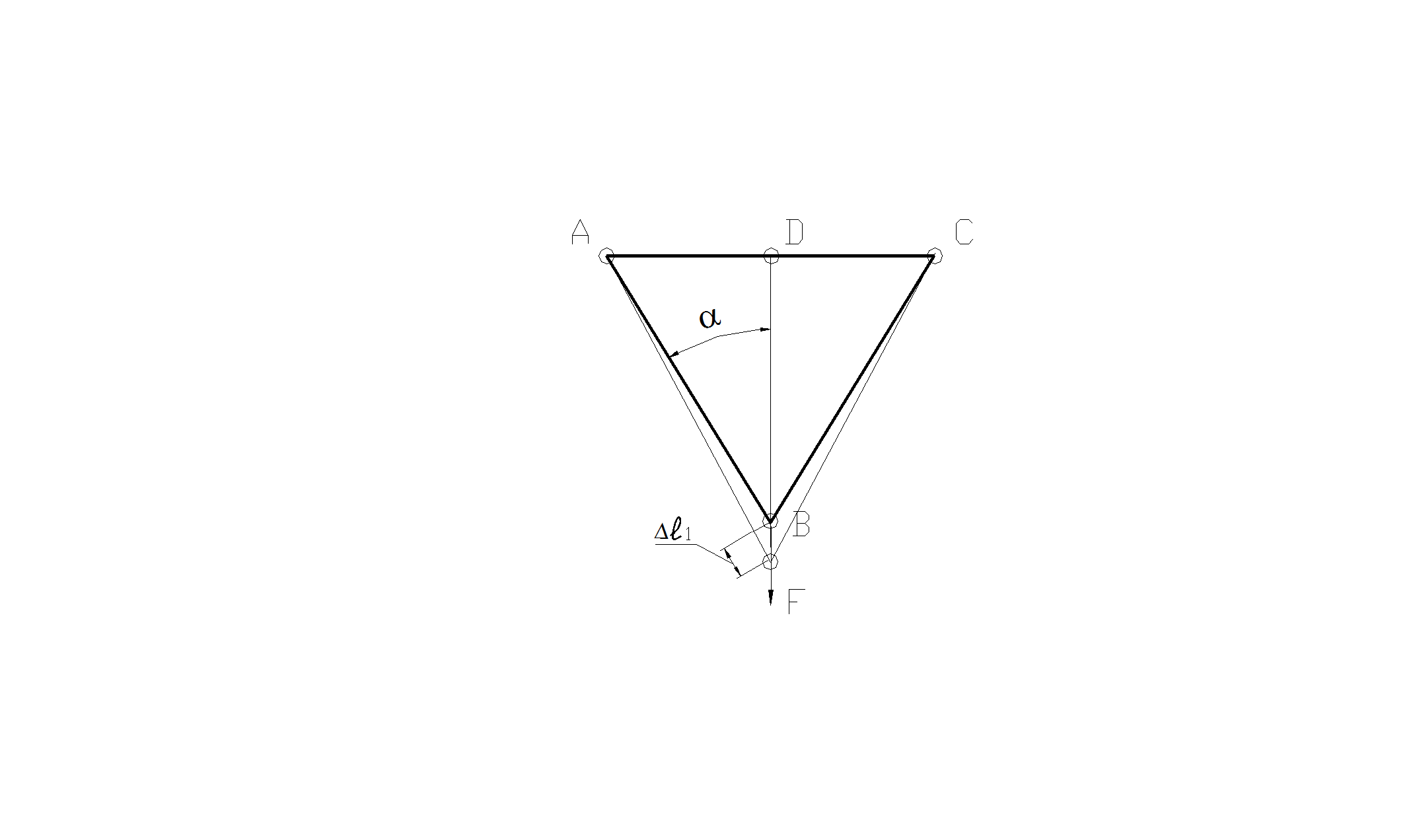
Рис.2.37

К примеру 2.11

Определим сначала действующие силы, составив уравнение сил

2N₁cosa+ N₂- F= 0.

При перемещении точки В имеет место соотношение Dl₁= Dl₂cosa , учитывая которое получим

N₁l₁/(Ef)= N₂l₂cosa/(Ef).

а так как из конструкции следует, что l₂= l₁cosa , то подставим его в предыдущее соотношение

N₁= N₂cos²a.

Следовательно,

N₂= F/(1+2cos³a); s₂= N₂/f; e₂= Dl₂/l₂= N₂ /(fE);

N₁= Fcos²a/(1+2cos³a); s₁= N₁/f, e₁= Dl₁/l₁= N₁/(Ef).

Отсюда вертикальное перемещение точки В равно

Dl₂= N₂l₂/(fE)= F l₂ /[(1+2cos³a) f E].

Пример 2.12: Определить напряжения в стержне на рис. 2.38

N₂

> Y

a Рис.2.38

о о К примеру 2.12

l F

F

>

x N₁

а) б)

Для решения задачи устраним нижнюю и верхнюю заделки, а их действие заменим силами реакции N₁ и N₂, значение которых заранее не известно. Для того, чтобы выразить эти силы через известную силу F, рассмотрим равновесие части, освобожденной от заделок.

Составим уравнение -N₂+ F- N₁=0.

Поскольку в приведенное уравнение входят 2 неизвестные, то введем дополнительное уравнение, учитывающее совместность деформации, т.е., что длина стержня не меняется Dl=0.

Так как стержень воспринимает сжимающие и растягивающие силы, то

D l= Fa/(Ef)- N₁ l/(Ef)= 0.

Откуда N₁= Fa / l.

Из уравнения равновесия сил получим

N₂= F- N₁= F(1-a/l)= F(l- a)/l

Напряжения будут равны

s₁= N₁/f; s₂= N₂/f.