Пружины.

В промышленности применяются разные пружины: витые (растяжения, сжатия рис. 2.40,а,б), плоские, тарельчатые (рис. 2.40,в), кольцевые (рис.2.40,г), рессоры (рис.2.40,д), стержневые (торсионные) (рис.2.40,е) и др. Они стандартизированы. Существуют и гидравлические пружины (рис.2.40,ж), в которых в качестве упругого элемента используется жидкость.

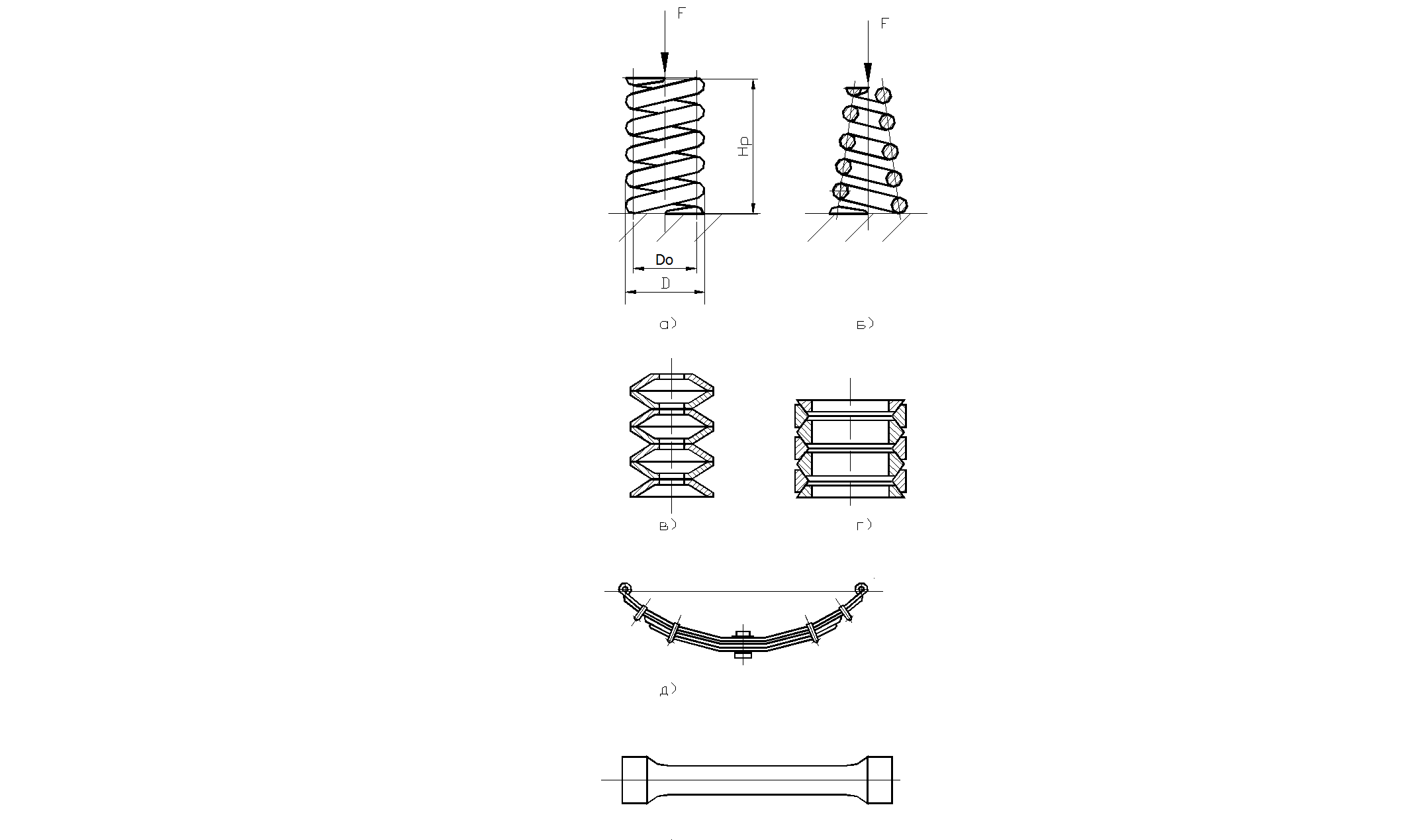
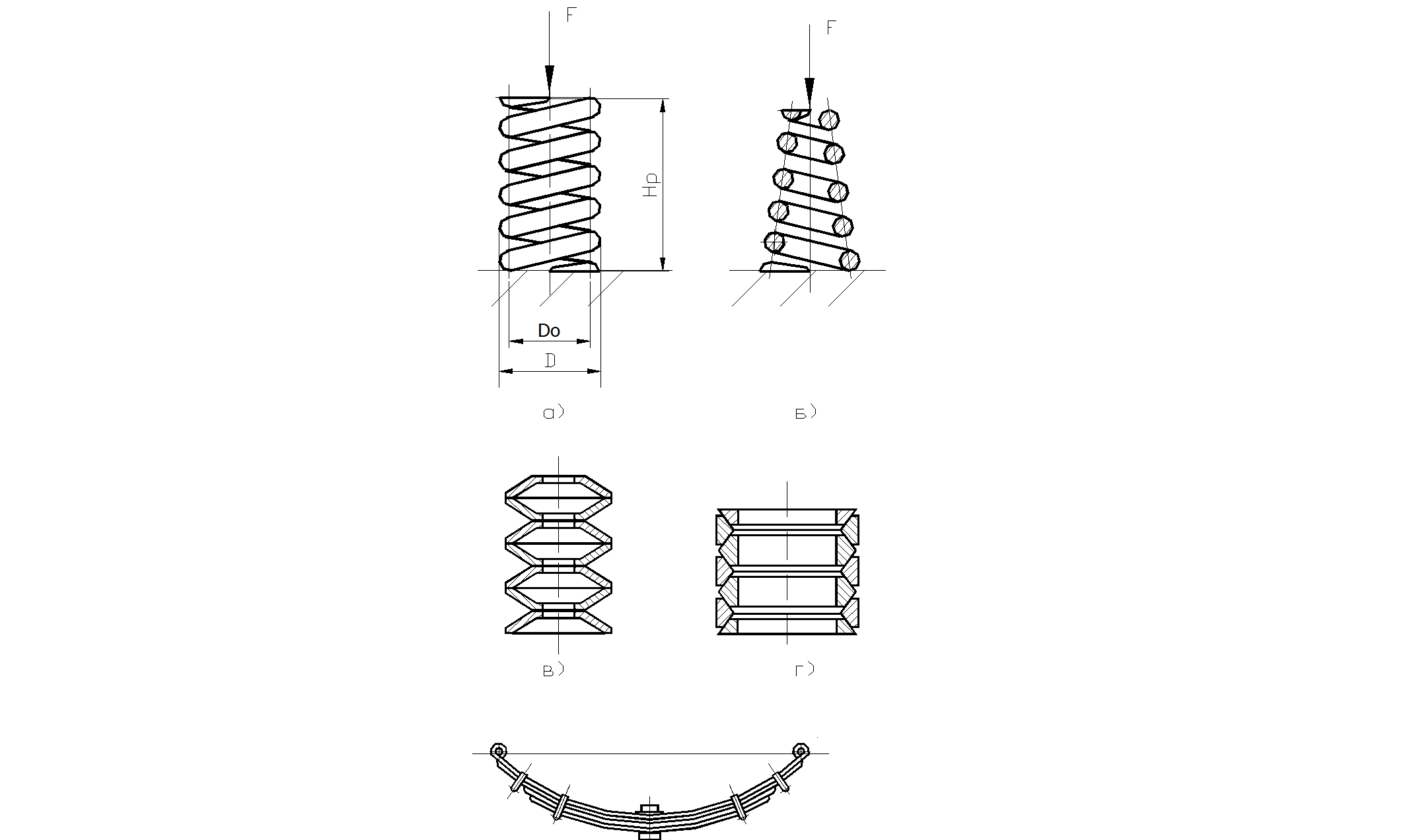
Рис. 2.40. Конструкции пружин: а) витая сжатия; б) витая фасонная; в) тарельчатая; г) кольцевая; д) рессора; е) стержневая; ж) гидравлическая.

Наиболее распространены витые или винтовые цилиндрические пружины, работающие на растяжение, сжатие. Рассмотрим их подробнее.

Витая пружина может рассматриваться как пространственно изргнутый брус, осевая линия которого в простейшем случае представляет собою винтовую линию с диаметром витка D₀ , числом витков z и углом подъема a; с_n = D₀/ d- индекс пружины; d- диаметр проволоки. При этом шаг пружины s= pD₀ tga. Обычно s<<pD_0.

Свойства пружины зависят от формы сечения проволоки и формы витка.

Конструктивной особенностью витых пружин является отделка концов, которые отгибаются таким образом, чтобы могло быть выполнено крепление пружины к смежным деталям.

Обычно величину c_n выбирают в зависимости от диаметра в следующих пределах

d, мм . . . . .до 2,5 3...5 6...12

с_n . . . . . . . . 5...12 4...10 4...9 .

Под действием силы F пружина деформируется (растягивается или сжимается). При этом в проволоке развиваются следующие максимальные касательные напряжения

t_max= KFD₀/(2W_к)£ [t_к ], (2-161)

где К= (4c_n- 1)/(4c_n- 4)+ 0,615/c_n- коэффициент, учитывающий кривизну витка и влияние поперечной силы; W_к - геометрический момент сопротивления сечения проволоки (для цилиндрической проволоки W_к= W_p=p d³/16 ).

Обычно пружины изготавливают из специального материала: сталей 60С2, 50ХФА ([t_к ]= 400- 750МПа); бронзы ([t_к ]= (0,2- -0,6)s_вр ).

Деформацию пружины можно рассчитать с помощью выражения

Dx= l_п F, (2-162)

где l_п= zpD³₀/(4GJ_к)- податливость пружины; z - число полных витков; G - модуль сдвига материала проволоки; J_к - геометрический момент инерции сечения для кручения (для цилиндрической проволоки J_к= J_р= p d⁴/32) .

На рис. 2.41 показана зависимость между нагрузкой и осадкой (деформацией) пружины сжатия).

Рис. 2.41. Диаграмма пружины сжатия

H₀= H₃+ z(s-d);

H₃= (z₁- 0,5)d

Также линейную деформацию можно описать выражением

Dx= F/C= Fl_пр/(fE_y )=FJ_пр, (2-163)

где l_пр= Н₀ – H₃ - длина пружины; Е_у = l_прС/f - условный модуль упругости; f= p(D²_н- D²_в)/4 - площадь сечения пружины; C= (F₂- F₁)/d - коэффициент жесткости пружины, определяемый по перемещению d конца при разности сил F₂- F₁; J_пр= l_пр/(fE_y)- коэффициент упругости.

Если пружину рассматривать как стержень сечением f, то под действием продольной силы в нем будут развиваться условные напряжения s_у= F/f= DxE_y/l_np. Эти выражения позволяют записать

s_у= {d³/[2D₀K(D²- D²_в)]}t_max. (2-164)

При проектировании диаметр проволоки определяют из выражения

d= 1,6(KFc_n/[t])^1/2. (2-165)

Так как жесткость одного полного витка равна l= pD³₀/(4GJ_к), то необходимое число витков можно оценить по упругому перемещению (ходу)

z= Dx/[l(F₂- F₁)]. (2-166)

Число витков округляют до полувитка при z£ 20 и до одного витка при z>20. Полное число витков

z₁= z+ (1,5...2).

Длина проволоки для изготовления пружины

L= pD₀ z₁/cos a » 3,2D₀z₁. (2-167)

При динамических колебаниях пружины уменьшают амплитуду колебаний и увеличивают демпфирование (подробней о динамике см. гл.3).