Сложное сопротивление.

Косой изгиб- имеет место, когда плоскость изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения (рис.2.31,а).

В этом случае разлагают изгибающий момент на два, действующих в главных плоскостях (проходят через главные оси сечения). Касательными напряжениями обычно пренебрегают.

M_z= F_yx= Mcosj; M_y= F_zx= Msin j.

В точке В сечения нормальные напряжения равны

s= M_yz/J_y+ M_zy/J_z= M(z sinj/J_y+ y cosj/J_z). (2-137)

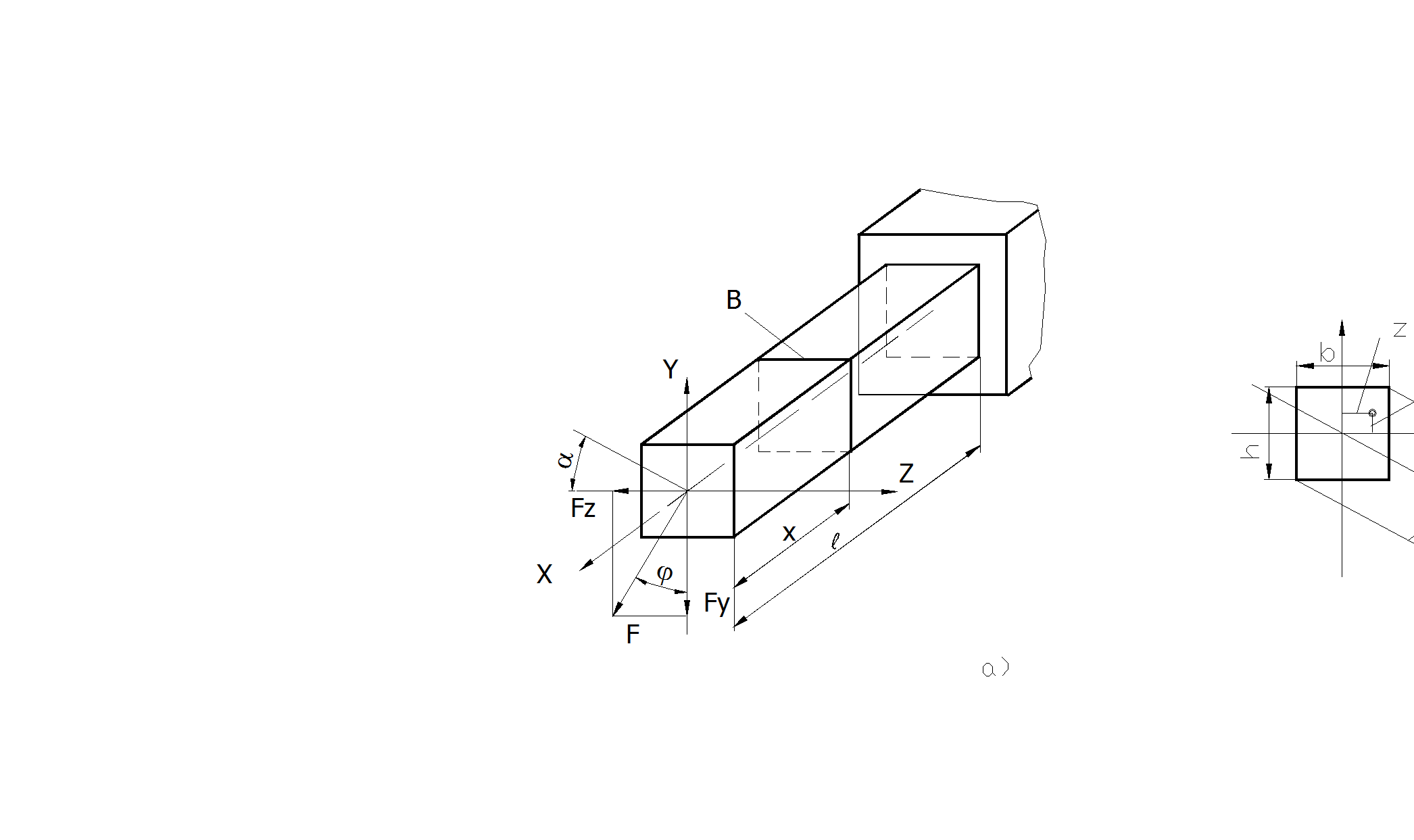
а) нейтральная линия

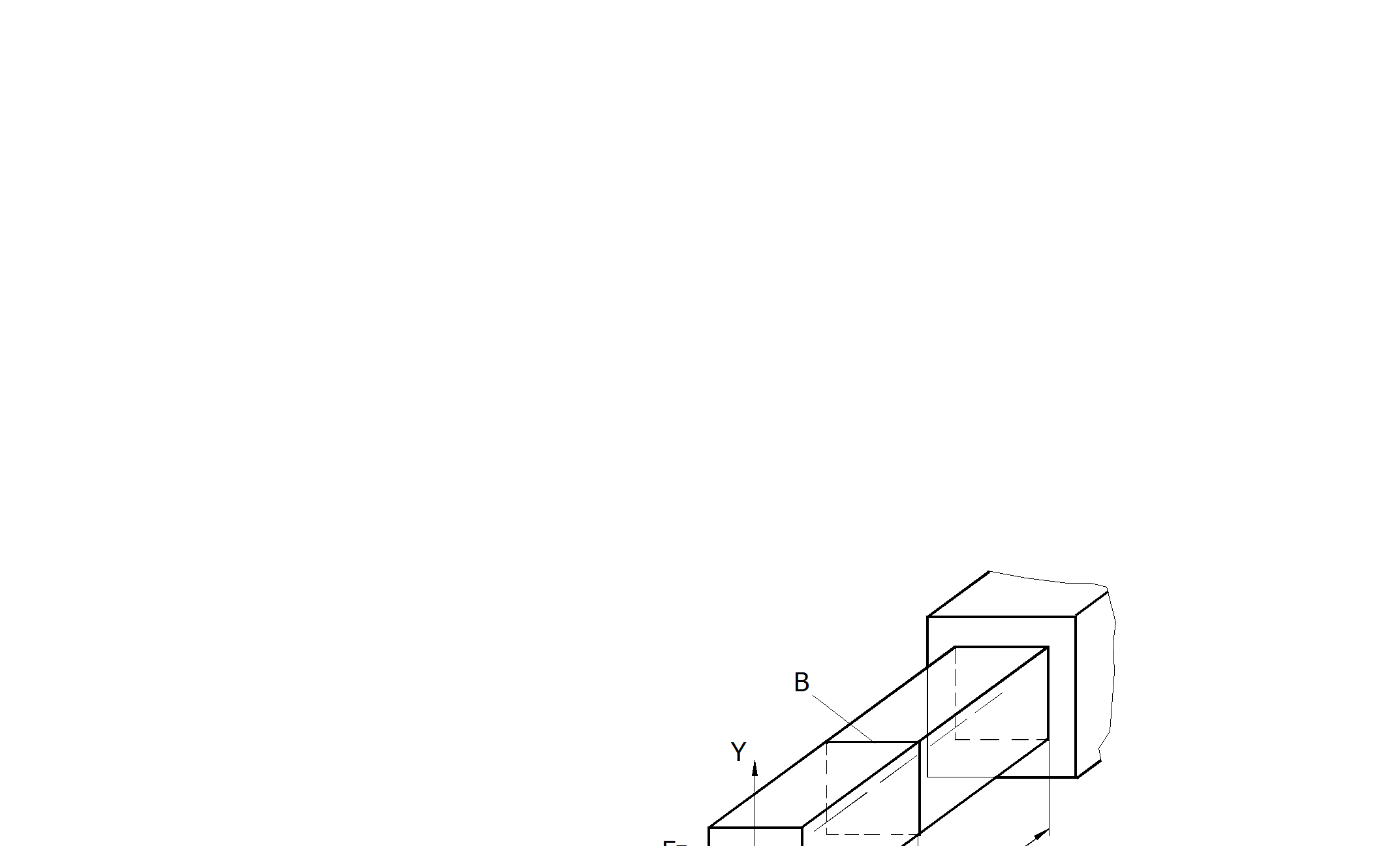
Рис.2.31

Сложный изгиб:

а) косой изгиб;

б) изгиб с внецентренным нагружением

б)

Положив в (2-137) s=0, найдем для нейтральной линии

y₀= - z₀ tgj(J_z/ J_y)

или

y₀/z₀= tga= - (J_z/J_y)tgj. (2-138)

т.е. нейтральная линия не перпендикулярна к плоскости момента, а несколько повернута в сторону оси минимального момента инерции.

Для круга, у которого J_z= J_y a=90°, получим

s_max= M_yz_max/J_y+ M_zy_max/J_z. (2-139)

Суммарный прогиб равен

d = (y²+ z²)^1/2. (2-140)

Изгиб с растяжением или сжатием (внецентренное нагружение) (рис. 2.31,б)

В сечении В консольно закрепленного стержня действуют

M_y= F_zx, Q_y= F_z; M_z= F_yx, Q_z= F_y.; N= F_x.

Полагая действия сил независимыми и пренебрегая касательными напряжениями, получим

s= N/f+ M_yz/J_y+ M_zy/J_z. (2-141)

Откуда

s_max = N/f+ M_y/W_y+ M_z/W_z. (2-142)

Кручение с изгибом.

Этот случай имеет место в зубчатых редукторах (рис. 2.32).

F_t1= F_t2; F_r1= F_r2; M_кр2= F_t2D₂/2; F_r1= F_t2tg20° .

Напряжения от кручения:

t_max= М_кр2/ W_p= M_кр2/(p d ³/16). (2-143)

Для изгиба в плоскости YАX от силы F_r (касательными напряжениями от перерезывающей силы пренебрегаем) получим

A_y+ B_y= F_r2;

A_yl- F_r2b= 0, т.е. A_y= F_r2b/l.

B_y= F_r2- A_y= F_r2a/l.

Следовательно, максимальный изгибающий момент в этой плоскости равен

M_umax1= A_ya= F_r2ba/l.

Откуда максимальные нормальные напряжения будут

s_ymax= M_umax1 /W_y= 32F_r2ba/(lp d³). (2-144)

Используя энергетическую теорию прочности, находим интенсивность напряжения

s_i= (s²_zmax+ s²_ymax+ 3t²_max)^1/2=

={[32F_t2ba/(lpd³) ]²+ [32F_t2ba/(lpd³)]²+ 3 [M_кр2/(pd³/16)]²}^1/2. (2-145)

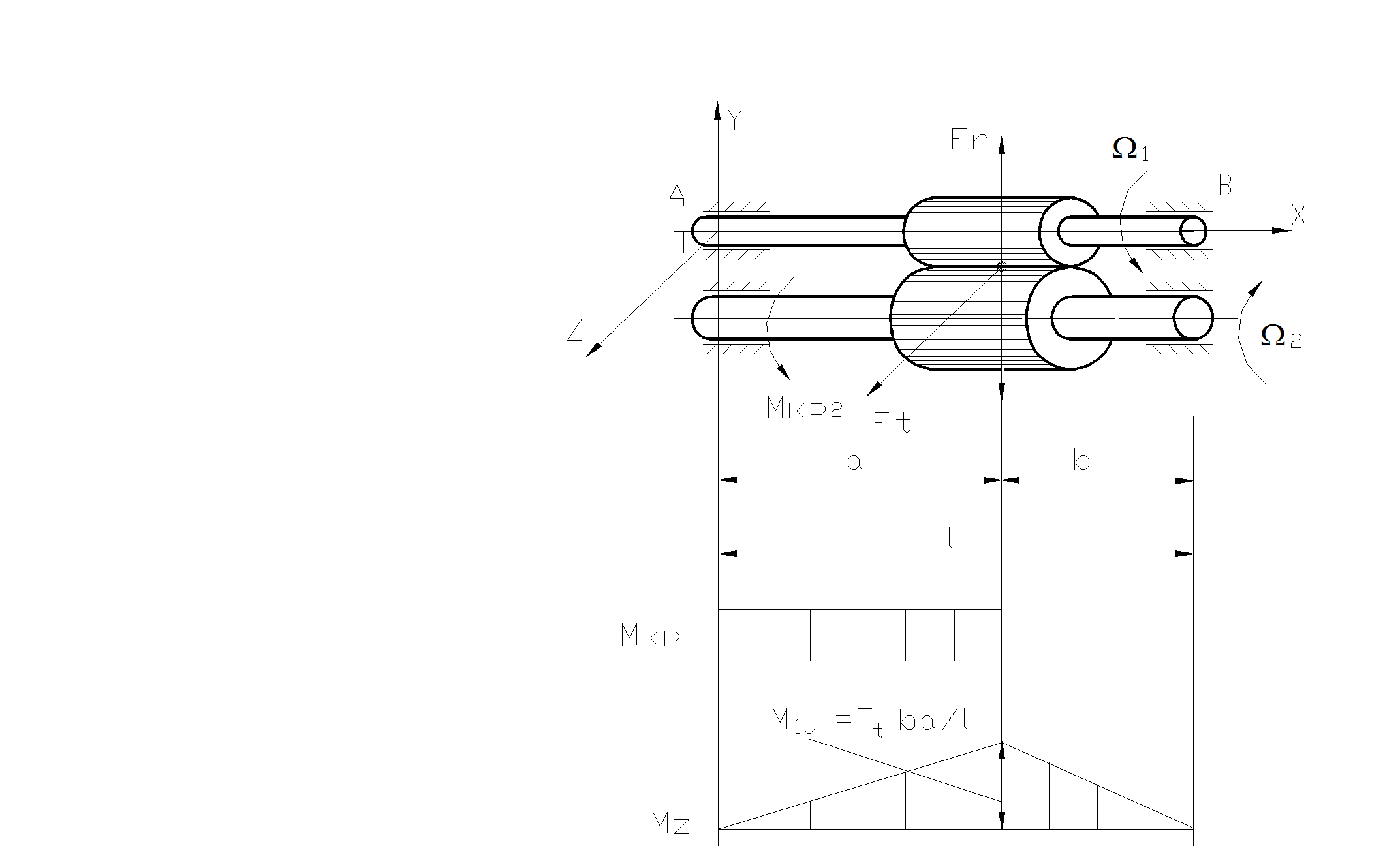
Рис. 2. 32. Кручение с

изгибом.

При этом должно быть

s_i£ [s_т].