Поперечный изгиб.

Рассмотрим балку (рис. 2.25), нагруженную распределенной по длине l нагрузкой интенсивностью q на единицу длины.

Вся нагрузка F= ql воспринимается двумя опорами А,Б. Причем опора А может совершать продольные перемещения. Поэтому F_А= F_Б= = ql/2, а продольная сила равна нулю.

От поперечной нагрузки в сечении действуют как перерезывающая (поперечная) сила, приводящая к касательным напряжениям t в сечении, так и нормальные напряжения s, обусловленные изгибом балки.

Разместим начало координат в точке А. Тогда связь перерезывающей силы с расстоянием x₁ от точки А можно описать уравнением

Q(x)= F_A- qx₁= ql/2- qx₁.

Изгибающий момент, действующий в каждой точке балки, описывается уравнением

M_z(x)= F_ax₁- qx₁x₁/2= qlx₁/2- qx²₁/2.

Это уравнение является выпуклой параболой. Из d M_z(x)/dx= ql/2- -qx₁=0 следует, что при x₁= l/2 будет максимум M_z= ql²/8, а при x₁= 0, x₁= l изгибающий момент M_z равен нулю.

Вырежем из балки элемент длиной dx (рис.2.25,б).

Пусть в левом сечении действует перерезывающая сила Q_y и изгибающий момент M_z. Тогда в правом будет - Q_y+ dQ_y; M_z+ dM_z.

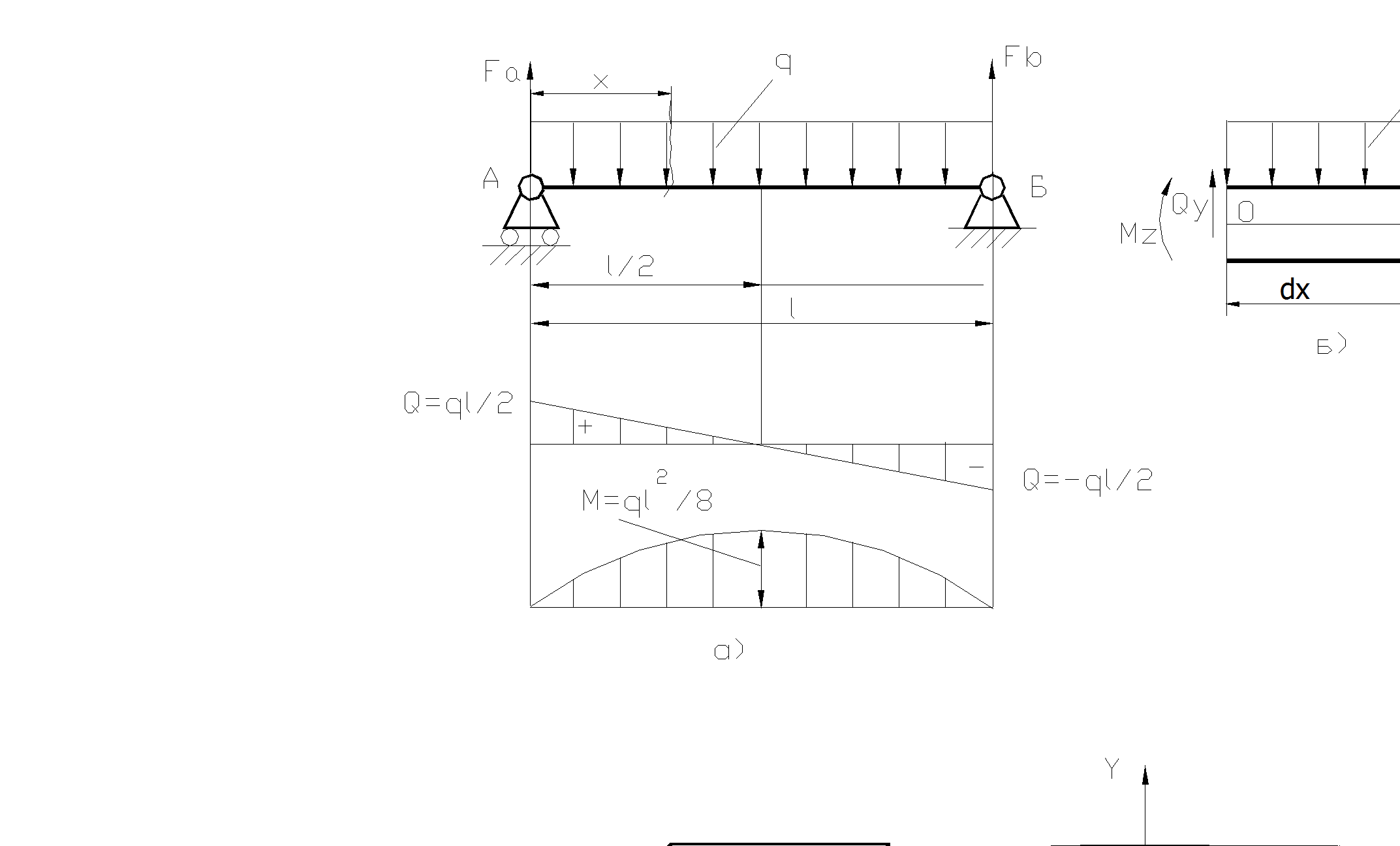
Рис. 2.25

Нагрузки при поперечном изгибе:

а) схема нагрузок и эпюры поперечной силы Q и изгибающего момента M;

б) силы, действующие на вырезанный элемент;

в,г) касательные напряжения в сечении балки.

Составим уравнения равновесия относительно точки О вырезанного участка

åM= M_z- (M_z+ dM_z)+ (Q_y+ dQ_y)dx+ qdxdx/2= 0;

åY= Q_y- qdx- (Q_y+ dQ_y ) = 0.

Из первого уравнения получим

-dM_z+ (Q_y+ dQ_y)dx+ qdxdx/2= 0.

Так как dQ_y<<Q_y, qdx² /2» 0, то можно записать

dM_z/dx= Q_y. (2-129)

Из второго уравнения следует

dQ/dx= -q. (2-130)

Также

d²M_z/dx² = -q. (2-131)

Касательные напряжения возникают не только в поперечном сечении, но и в продольных сечениях (рис. 2.25,в). Они искажают форму сечения. В большинстве случаев этим пренебрегают.

Величину касательных напряжений при поперечном изгибе можно рассчитать по формуле Журавского

t= (dM_z/dx)S^*_z/(J_zb)= QS^*_z/(J_zb), (2-132)

где S^*_z -статический момент сечения; b - ширина балки.

Так для прямоугольника получено

t= 6Q(h²/4- y²)/(bh³). (2-133)

Это параболическая зависимость (см. рис.2.25,г).

При y=0 t_max= 1,5 Q/(bh), (2-134)

а при y= h/2 t=0.

Максимальные нормальные напряжения равны (см. (2-111))

s_max= M_z/W_z= 6Fl/(bh²).

Откуда при Q= F

s_max/t_max= [6Fl/(bh²)][ 1,5 Q/(bh)]= 4l/h,

т.е. при l>h t @ 0. Поэтому обычно касательными напряжениями пренебрегают.

В круге будет

t_max= (4/3)Q/(p r²). (2- 135)

Для оценки прочности стержня надо знать s_max , t_max. При этом в точках волокон, наиболее удаленных от нейтрального слоя, действуют лишь нормальные напряжения, а в точках нейтрального слоя- касательные. В других точках сечения действуют оба вида напряжений.

Пример 2.5.

При расчете балок принято правило знаков, изображенное на рис. 2.26

1. Для балки сечением b₁h на рис. 2.27 построить графики изменения по длине поперечной силы и изгибающего момента - эпюры поперечной силы и изгибающего момента.

Из уравнения равновесия моментов относительно точки А получим

åM= F_bl - F_aa= 0.

Откуда

F_b= Fa/l.

Из уравнения равновесия моментов относительно точки В получим

F_al - F_bb= 0.

Откуда F_a= Fb/l.

C учетом правила знаков составим уравнения перерезывающих сил и изгибающих моментов.

Для левого участка x₁<a

Q_y(x₁)= F_a= Fb/l.

M_z(x₁)= F_ax₁= Fbx₁/l.

Для правого участка x₂> a

Q_y(x₂)= F_a- F= F(b/l-1)= F(b-l)/l.

M_z(x₂)= F_ax₂- F(x₂- a)= Fbx₂/l - F(x₂- a).

Эпюры или графики изменения по длине балки сил и моментов показаны на рис. 2.27.

Максимальный изгибающий момент будет при х= а M_znax= Fba/l.

При этом максимальное нормальное напряжение равно

s_max = M_zmax/ W_z= Fbal^-1/W_z. (2-136)

Если сечение балки прямоугольник, то W_z= b₁ h²/6, тогда

s_max = Fbal^-1/ (bh²/6)= 6Fba/(b₁h²l).

Если сечение круг диаметром d, то s_max= 32Fbal^-1/(pd³)

Для кольца получим

s_max = 32Fbal^-1/ [(pd³₁)(1- d⁴₂ /d⁴₁)],

где d₁, d₂ соответственно наружный и внутренний диаметры кольца.

Максимальное касательное напряжение равно для прямоугольника

t_max= 1,5 Q/(bh).

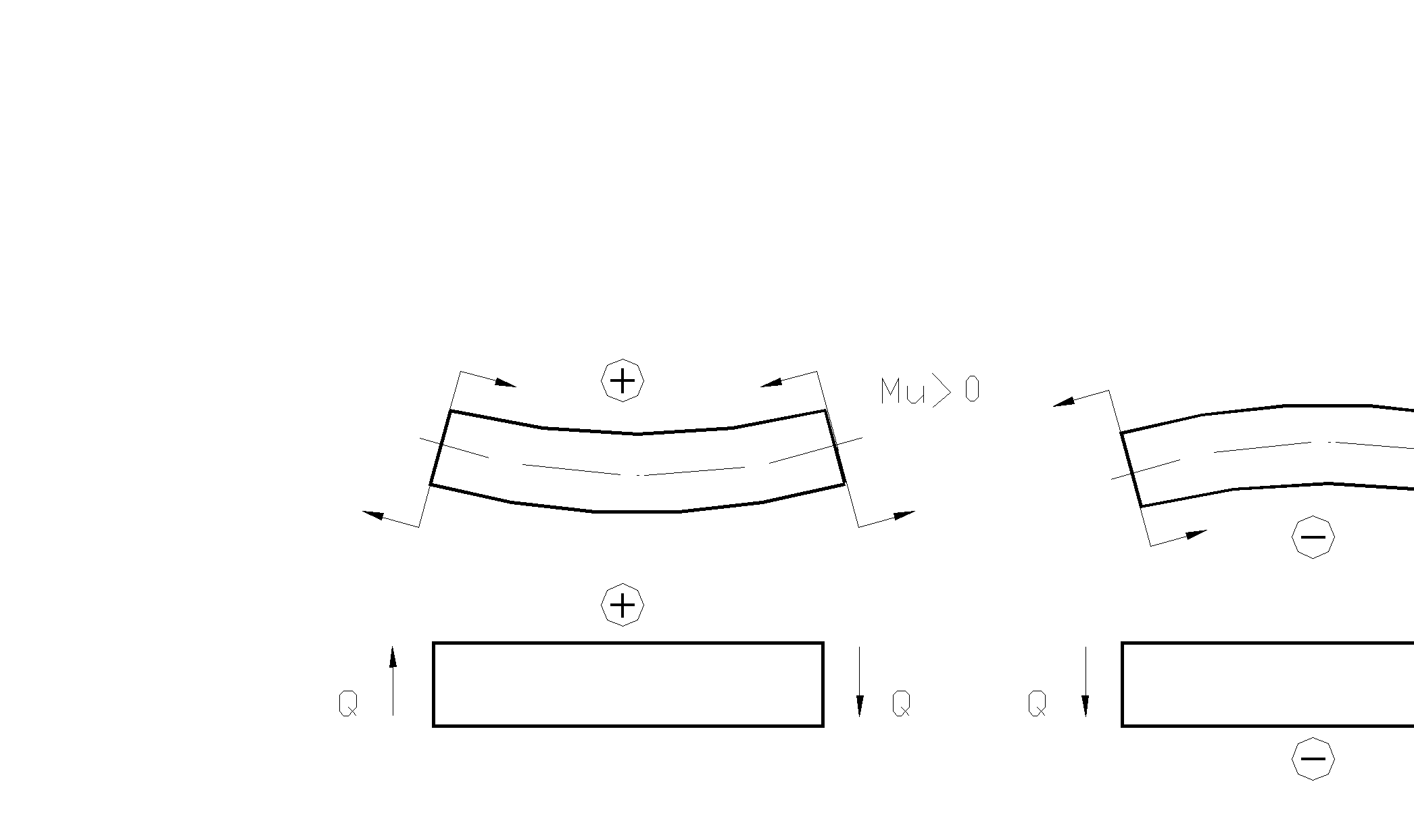
Рис. 2.26. Правило знаков.

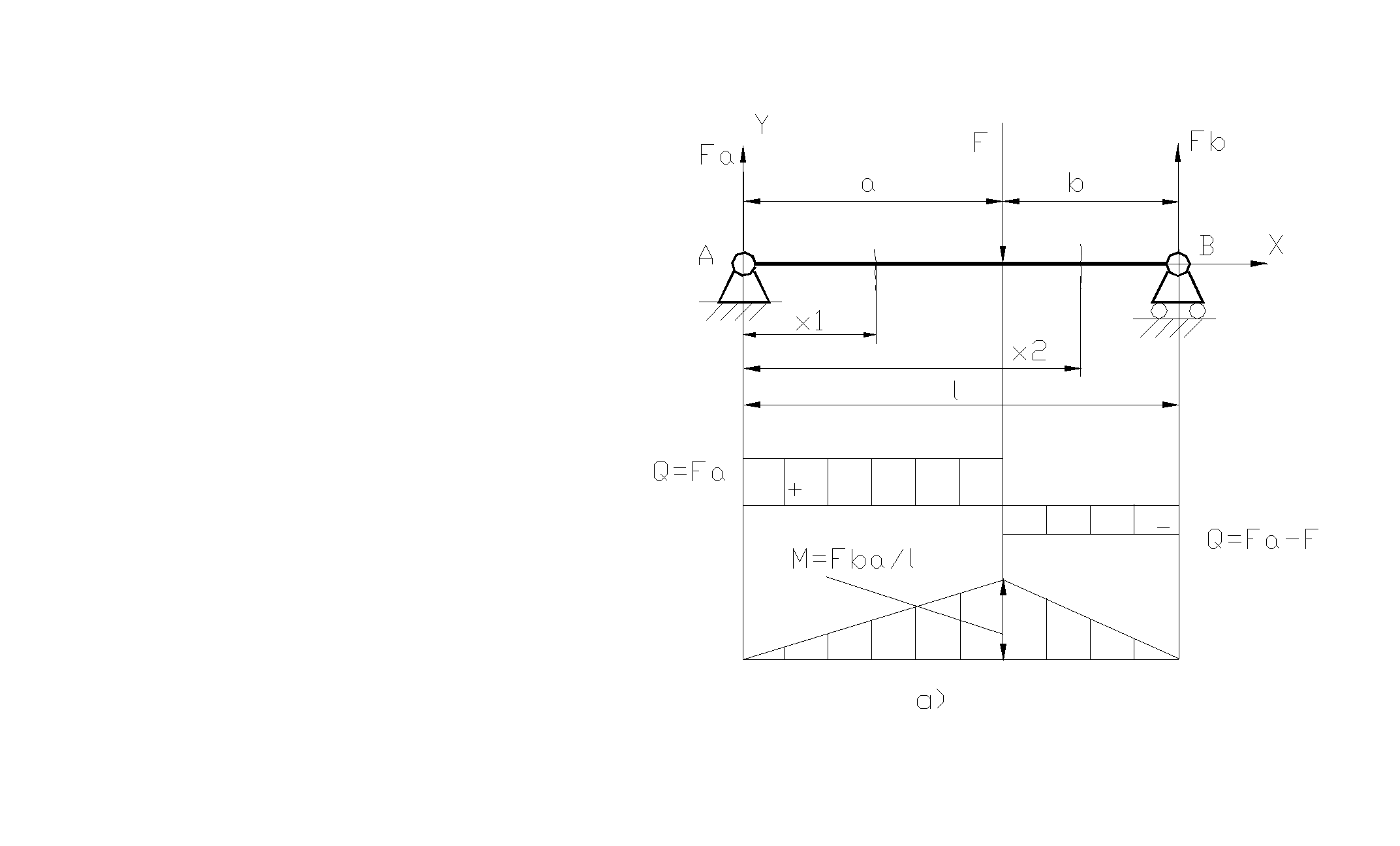
Рис. 2.27. Расчет балки

Пример 2.6:

Дано: Балка с нагрузками, как на рис. 2.28;

F= 1,6 кН; q= 0,2 кН/м; a= 2,5 м; b= 1,25 м; с= 1,25 м.

Допускаемое напряжение [s]= 110 Н/мм².

Построить эпюры перерезывающей силы и изгибающего момента.

Определить диаметр балки.

Из уравнения моментов относительно опоры В определим реакцию F_A в опоре А

F_A *5= 0,2*2,5*3,75+ F*1,25

F_A= 0,375+ 0,25F= 0,775 кН.

Из уравнения моментов относительно опоры А определим реакцию F_В в опоре В

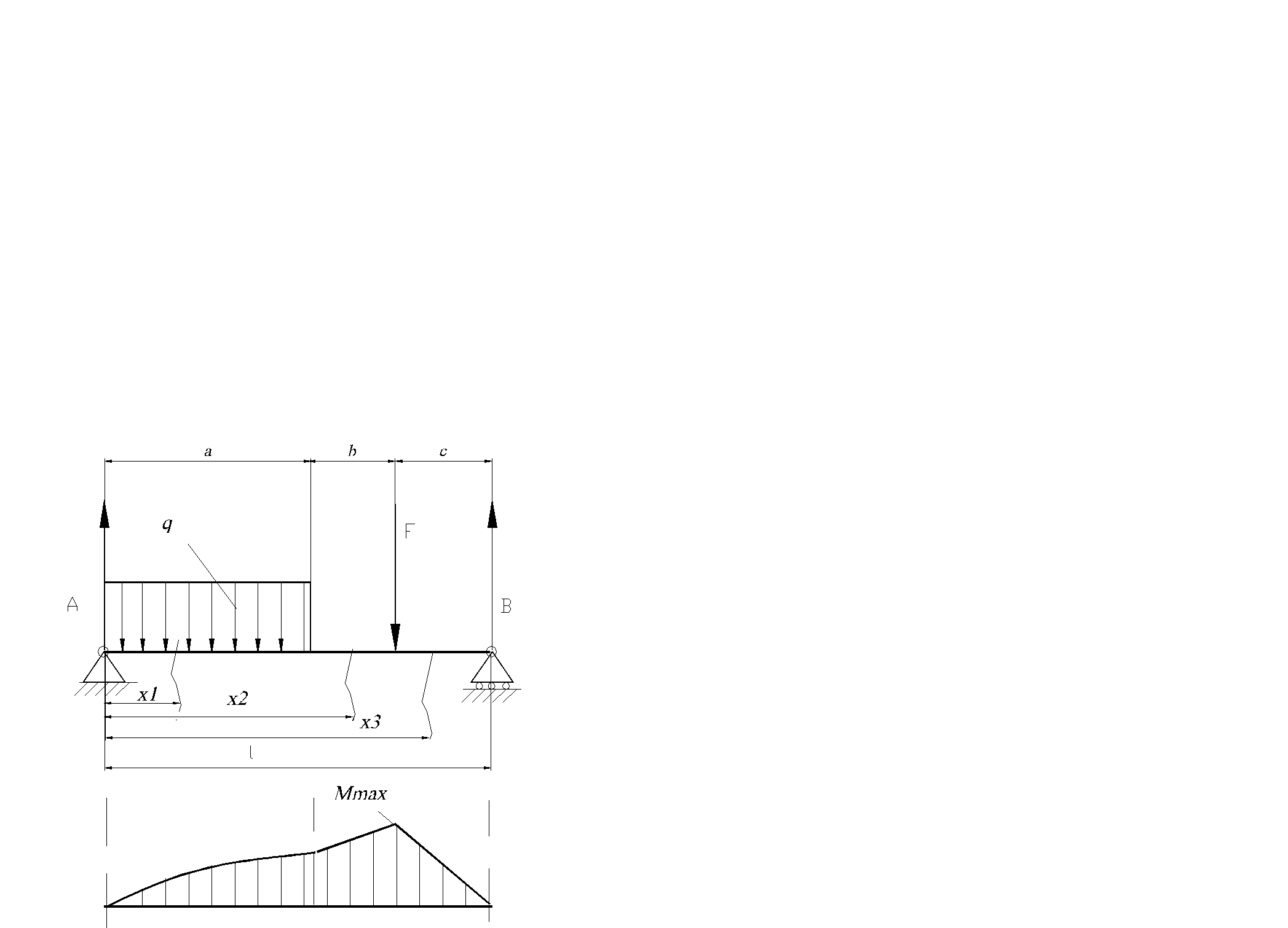
Рис. 2.28 Балка.

F_В *5= F*3,75+ 0,2*2,5*1,25= 6,625 кН.

Составим уравнения моментов на 1-м участке

M(x₁)= F_Ax₁- qx²₁/2= 0,775x₁- 0,1x²₁.

Составим уравнение поперечных сил

Q(x)= F_a- qx= 0,775- 0,2x.

Составим уравнение моментов на 2-м участке

M(x₂)= F_Ax₂- q*2,5(x₂-1,25)= 0,775x₂- 0,5(x₂- 1,25)= 0,275x₂ + +0,625 .

Составим уравнение поперечных сил

Q(x)= F_a- qа= 0,775- 0,5= 0,225 кН.

Составим уравнение моментов на 3-м участке

M(x₃)= F_Ax₃- q*2,5(x₃-1,25) – F(x₃ – 3,75)= 0,775x₃ - 0,5(x₃ - 1,25) – -F(x₃ - 3,75)= -1,325x₃ + 6,625 .

Составим уравнение поперечных сил

Q(x)= F_a- qа- F=0,225- 1,6= - 1,375 кН.

При x₂= 2,5 M(x₂)= 1,31 кНм

При x₂= 3,75 M(x₂)= 1,66 кНм

При x₃= 3,75 M(x₃)= 1,66 кНм.

При х₃= 5 М(х₃)= 0.

Т.е. М_мах= 1,66 кНм. Тогда

d= [М_мах/(p [s]/32)]^1/3 ={ 1,66*32*10⁵/(3,14*110)}^1/3 » 24,87 мм.

Пример 2.7:

Дано: Балка с нагрузками на рис. 2.29; F₁= F₂= 800 Н;

q= 1200 Н/м; a= 1 м; b= 2м; с= 1,5 м; балка имеет прямоугольное сечение b₁x h= 150x300 мм.

Определить максимальное напряжение.

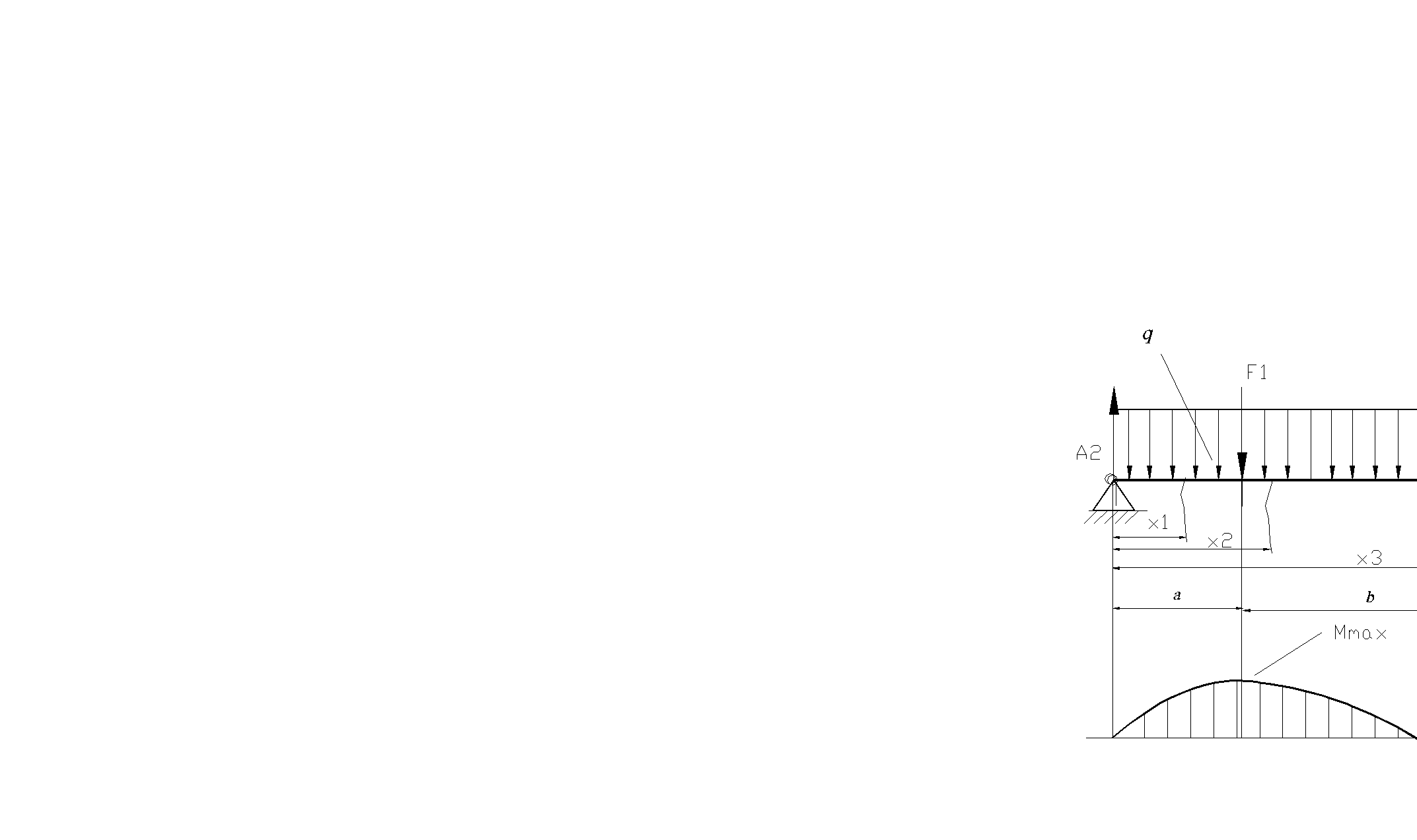
Рис. 2.29

Балка с нагрузками и эпюрой изгибающего момента.

Из уравнения моментов относительно опоры В определим реакцию F_A в опоре А

F_A *3 – 1200*3*1,5- 800*2 + 800*1,5= 0;

F_A = (1200*4,5+ 800*0,5)/3= 1933,3 Н.

Из уравнения моментов относительно опоры A определим реакцию F_B в опоре B

F_B *3 = 800+1200*3*1,5+ 800x4,5= 9800.

F_B = 3267 Н.

Составим уравнения моментов на 1-м участке

M(x₁)= F_Ax₁- qx²₁/2=1933x₁- 600x²₁.

Составим уравнения моментов на 2-м участке

M(x₂)= F_Ax₂- q*x² ₂ /2 –F₁(x₂- 1) =1933x₂- 800(x₂- 1) – 600x²₂ = = 1133x₂ - 600x²₂ + 800 .

Составим уравнения моментов на 3-м участке

M(x₃)= F_Ax₃- q*3*(x ₃ – 1,5) –F₁(x₃- 1) + F_B(x₃- 3) =1933x₃- -3600(x₃- -1,5) - 800x₃ + 800+ 3267x₃- 9800= 800х₃ -3600 .

При x₂= 1м M(x₂)= 1333 Нм

При x₂= 3м M(x₂)= -1200 Нм

При x₃= 3 м M(x₃)= - 1200 Нм.

При х₃= 4,5 М(х₃)= 0.

Т.е. М_мах= 1333 Нм. Тогда

s_мах= М_мах/ (b₁h²/6)= 6*1333*10³/(150*300²)= 0,59 Н/мм²= =0,59МПа.