Сдвиг и кручение.

Если на стержень действуют силы, как это показано на рис. 2.16,а, то при малом расстоянии между силами F заштрихованный участок наклонится. Поскольку на стержень действуют только поперечные силы, то в сечении между F-F разовьются только касательные напряжения t, уравновешивающие указанные воздействия. Это изображено на рис. 2.16,в.

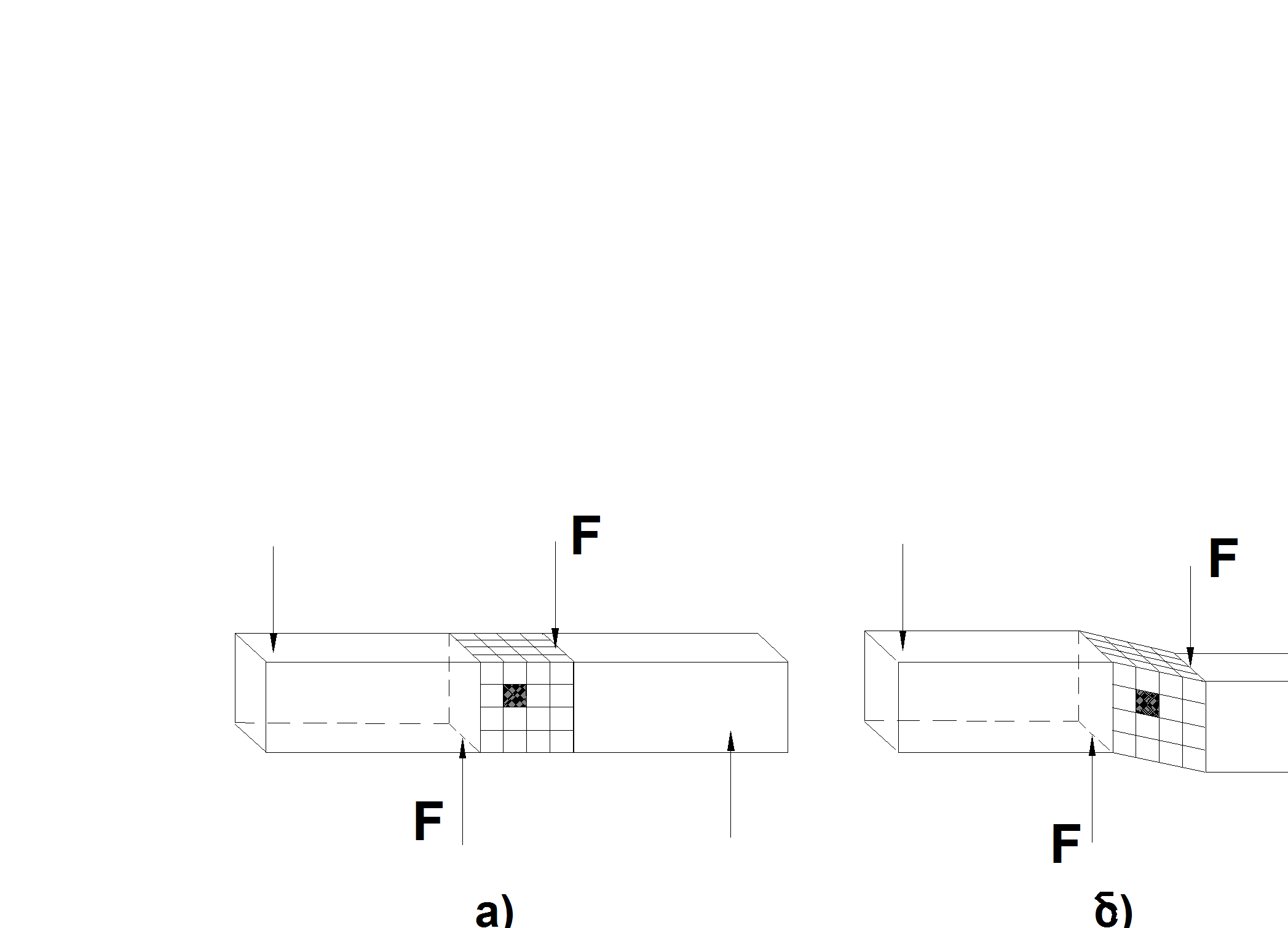
а) б) в)

Рис. 2.16 Схема деформации и внутренние силы (напряжения)

при сдвиге стержня.

Принимая распределение касательных напряжений t равномерным по сечению площадью f, их величину определяют из соотношения

t = F/f. (2-82)

Величина этих напряжений должна быть меньше допускаемых значений, т.е. t £ [t].

Если на участке между силами F выделить прямоугольник и рассмотреть его после отмеченного изгиба, то на гранях образованного параллелограмма возникнут касательные напряжения, как показано на рис. 2.17.

Рис. 2.17

Напряжения и деформации элемента при сдвиге

Такое напряженное состояние называют чистым сдвигом. Величина а называется абсолютным сдвигом. Угол g, на который изменяются прямые углы, называют относительным сдвигом

tgg @ g = a/h. (2-83)

Экспериментально установлено, что

a= Fh/(Gf), (2-84)

где G- является коэффициентом пропорциональности и называется модулем сдвига (для стали G= 8*10⁴ МПа).

Учитывая (2-82) и (2-83), из (2-84) получим закон Гука при сдвиге

t =Gg. (2-85)

Между модулем продольной упругости и модулем сдвига имеется взаимосвязь

G= 0,5E/(1+c)@ 0,4 E.

Чистый сдвиг реализовать весьма сложно, т.к. практически всегда будут и другие напряжения.

Достаточно часто сдвиг проявляется при кручении, это такой вид деформации, когда в поперечных сечениях действует только крутящий момент, а остальные силы отсутствуют.

Если рассматривать кручение цилиндрического стержня (рис. 2.18), то сечения, удаленные от точки закрепления на расстояние х будут поворачиваться друг относительно друга на некоторый угол j, измеряемый от оси вращения. Тогда на расстоянии x+ dx угол поворота будет j+ dj .

Полагая образующие прямыми, получим

È È È

tgg= (CC₁- BB₁ )/ BC= [r (j +dj)- rj]/dx= rdj /dx= r q.

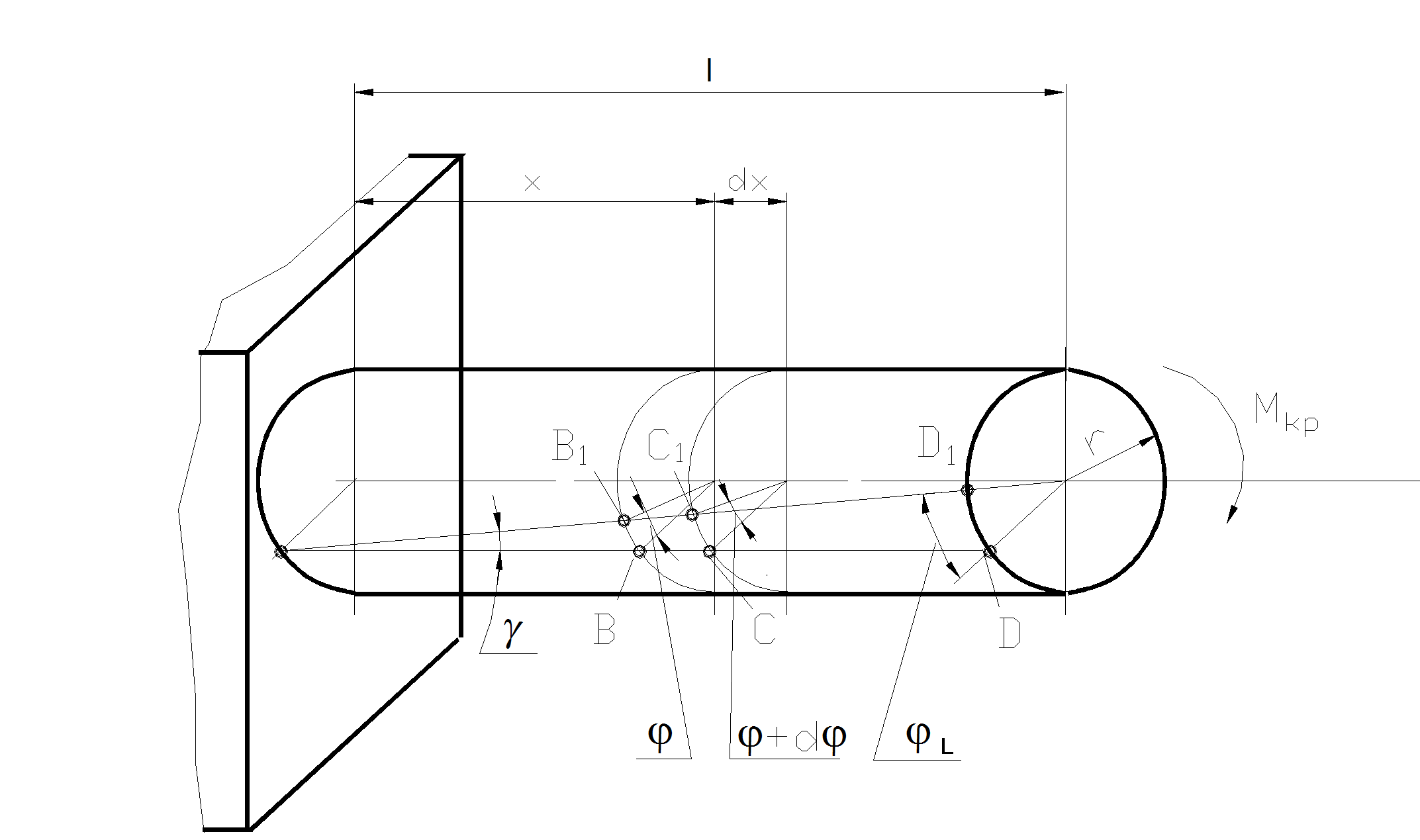
Рис.2.18 Скручивание стержня.

Отношение dj/dx называется относительным углом закручива-ния и обозначается буквой q. Тогда

tgg» g= rq . (2-86)

Из закона Гука (2-85) следует

t= Gg = Gq r. (2-87)

Таким образом, в любой точке сечения стержня касательные напряжения равны t_r = Gq r, где r - радиус точки относительно оси вращения. Следовательно, на поверхности стержня касательные напряжения будут максимальными.

Выделим элементарную площадку размерами df= rdjdr в сечении стержня. Момент касательных сил на этой площадке относительно оси вращения dM_кр= t_r r df.

Тогда по всему сечению получим

М_кр= 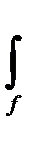t_r r df.

Учитывая (2-87), запишем

М_кр= 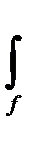Gq r² df= Gq 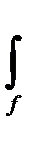r² df.

Интеграл 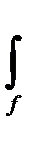r²df = J_p называется полярным моментом инерции сечения. Поэтому

М_кр= Gq J_p. (2-88)

Поскольку df= rdjdr, тодля круга

J_p = 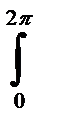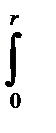r³djdr= 2p 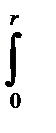r³dr= 2pr⁴/4= p r⁴/2= pd⁴/32 . (2-89)

Для кольца будет

J_p = 2p 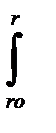r³dr= p r⁴ (1- r₀ ⁴/r⁴) /2= pd⁴ (1- d₀ ⁴/d⁴) /32,. (2-90)

где r₀, d₀- радиус и диаметр отверстия в кольце.

Для прямоугольника, расположенного симметрично относительно центра тяжести и имеющего df= b dy , где b – ширина по оси х; y -координата по высоте, равной h, получим

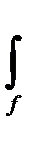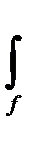J_p = r²df= y²df+ 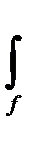х²df = b 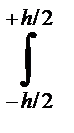y²dy + h 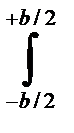x²dy = by³/3| +

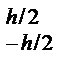+ hx³/3| 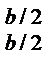= bh³/12+ hb³/12 = hb(h²+ b²)/12. (2-91)

Из (2-88) определим относительный угол закручивания стержня любой формы

q= М_кр/ (GJ_p). (2-92)

Откуда закручивание стержня длиной l будет

j_l = 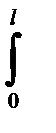М_крdx/ (GJ_p)= М_крl/ (GJ_p). (2-93)

Если по длине стержня переменного сечения действуют разные моменты кручения, суммарный угол закручивания можно определить из соотношения

j_l = 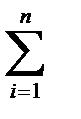М_крi l_i/ (G_i J_pi). (2-94)

Подставив в (2-87) q= М_кр/ (GJ_p), определим величину касательных напряжений в любой точке сечения, расположенной на радиусе r

t= Gr М_кр/ (GJ_p) = M_крr /J_p, (2-95)

а для точек, находящихся на поверхности стержня это будет максимальное значение касательного напряжения

t_max = M_кр /W_p , (2-96)

где W_p= J_p/r - называется полярным моментом сопротивления сечения.

В работающих конструкциях должны выполняться условия

t_max £ [t]; j£ [j], (2-97)

где значения в квадратных скобках называются допускаемыми.

Полагая, что при закручивании стержня в пределах упругости изменение потенциальной энергий от деформации будет dE_p= 0,5M_крdj, для элементарного участка длиной dx запишем dj= М_кр(GJ_p)^-1dx, тогда

dE_p= 0,5M²_кр(GJ_p)^-1dx. (2-98)

В этом случае потенциальная энергия стержня длиной l составит

E_p= 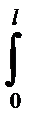0,5M²_кр(GJ_p)^-1dx= 0,5 M²_кр(GJ_p)^-1l. (2-99)

Это выражение получено в предположении постоянства по длине стержня G, J_p.

Подставим в (2-98) М_кр= t_мах W_p и разделим на dV= fdx

w_n = 0,5(t_мах W_p)² /(fGJ_p)=0,5t ²_махW ²_p /(fGJ_p)=

= 0,5t ²_махJ_p /(fGy²_max)=0,5t ²_мах k_fJ /G, (2-100)

где k_fJ = J_p/(fy²_max); y²_max - максимальная ордината сечения.

Величина w_п представляет собой потенциальную энергию, накопленную в элементарном объеме скручиваемого стержня.

Для круга при k_fJ = J_p/(fy²_max)= 0,5pr⁴/(pr²r²)= 0,5 он

аравна

w_п =0,25t²_махG^-1. (2-101)

Изгиб.

Чистый изгиб

Рассмотрим балку, один конец которой закреплен в стенке ( это называется заделкой), а на другой, свободный, действует в плоскости чертежа только изгибающий момент (рис. 2.19). От него балка изгибается.

Из теории упругости известно, что уравнение изогнутой оси записывается в форме

y= x² M_u/(2EJ_z). (2-102)

Это парабола.

Продифференцируем это уравнение по х

dy/dx= x M_u/(EJ_z); d²y/dx²= M_u/(EJ_z). (2-103)

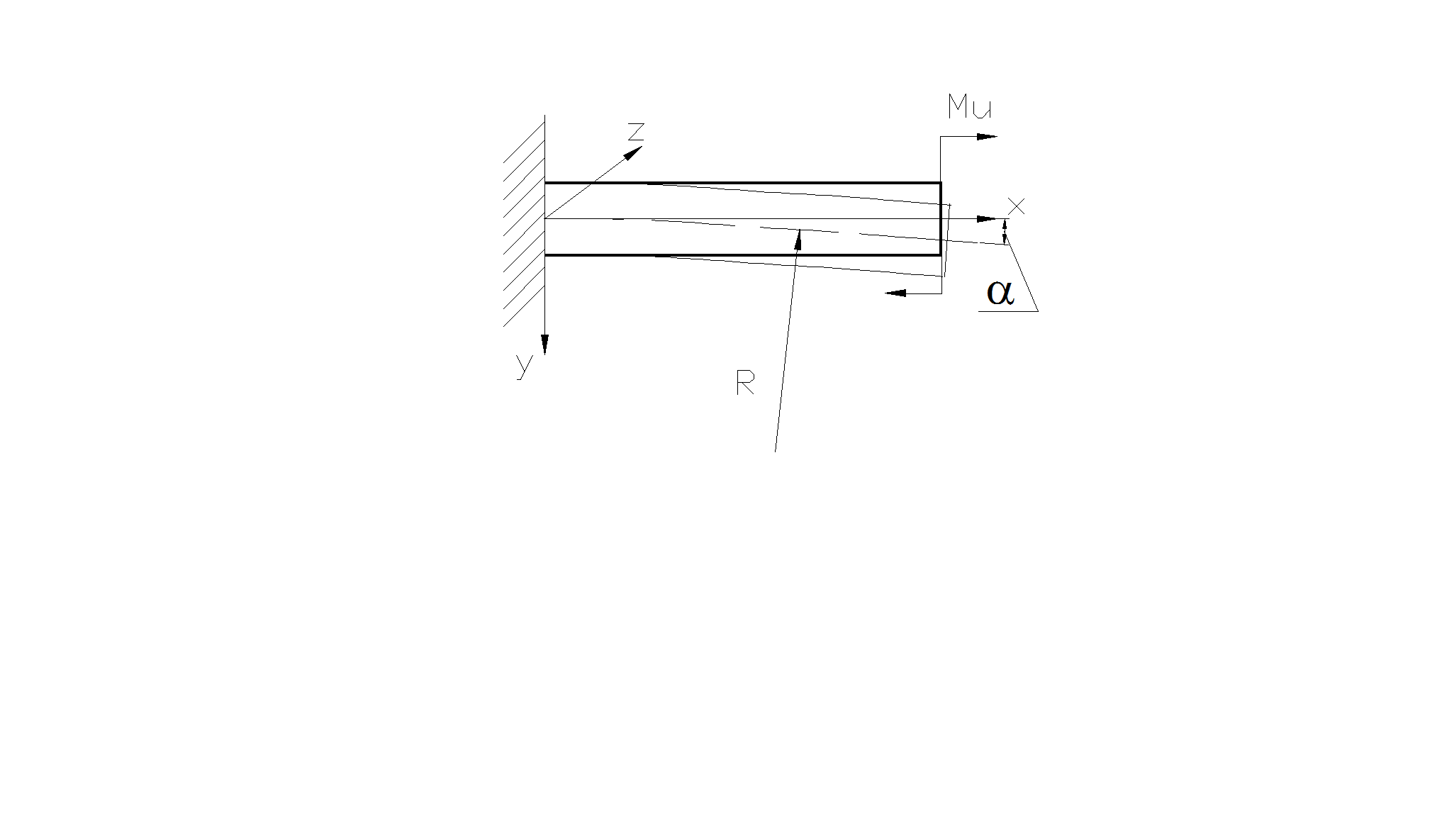
Рис.2.19 Чистый изгиб балки

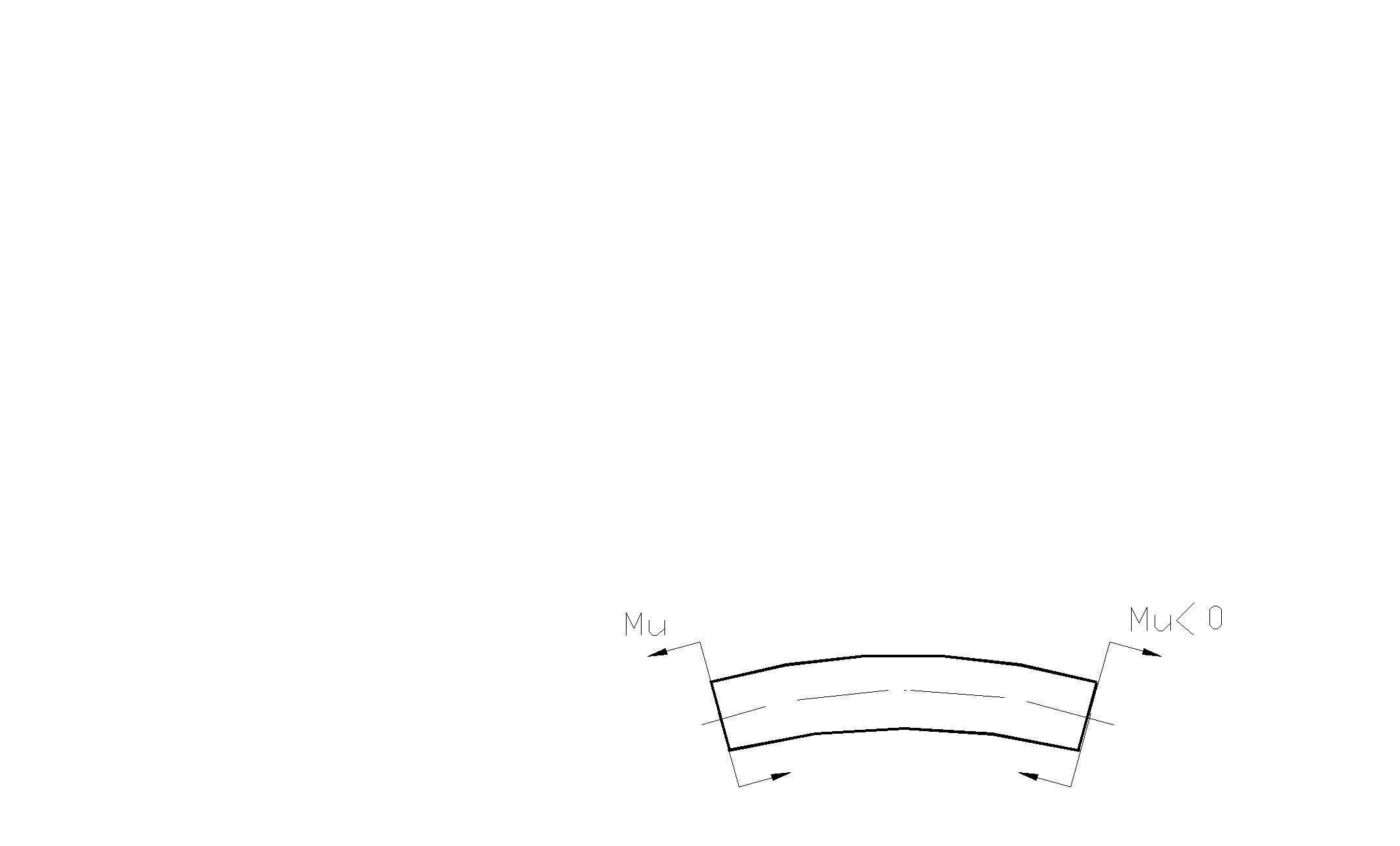
Рис. 2.20 Напряжения при чистом

изгибе

Заметим, что dy/dx= tga » a , где a - угол поворота оси балки; J_z= 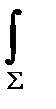y²df; df- элементарнаяплощадь сечения стержня. Е- модуль проольной упругости.

Сомножитель J_z называется моментом инерции поперечного сечения å относительно оси z.

Из (2-103) следует, что при действии только изгибающего момента М_и d²y/dx²=const.

Поскольку в математике величина d²y/dx² связана с кривизной в точке какой-либо изогнутой кривой соотношением d²y/dx²» 1/R, где R- радиус кривизны в точке кривой, то можно записать

d²y/dx²» 1/R= M_u/(EJ_z). (2-104)

Если мысленно отделить балку от заделки и заменить заделку противонаправленным изгибающим моментом М_и (рис. 2.20), то выше линии, проходящей по центрам тяжести сечений балки- нейтральной оси, будем иметь растягивающие напряжения (+s), а ниже- сжимающие - (-s).

При чистом изгибе в сечениях действуют только нормальные (перпендикулярные к поперечному сечению) напряжения.

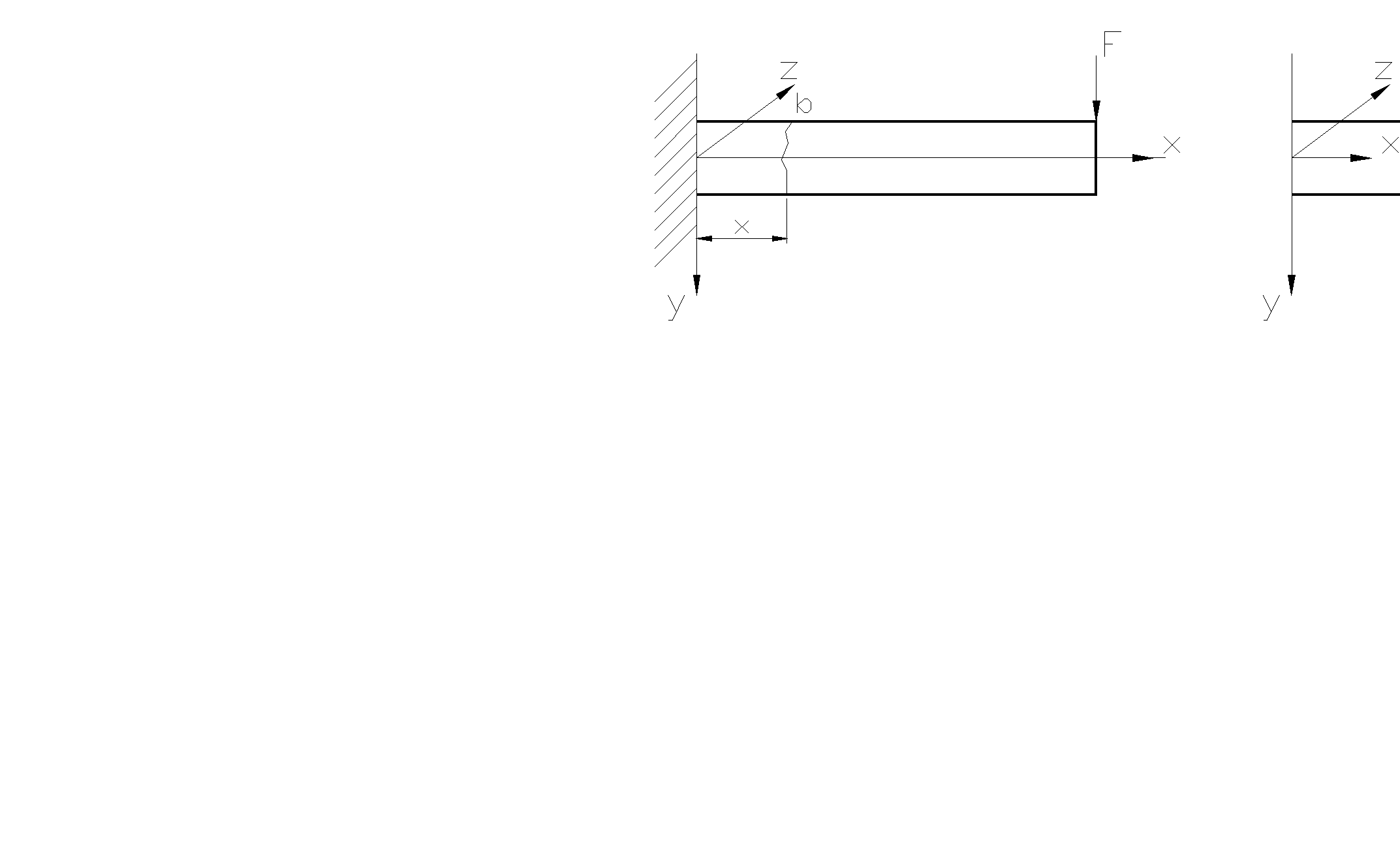
Рис. 2.21 Изгиб от поперечной силы

Чаще встечаются более сложные случаи, когда действуют не только изгибающие моменты, но и поперечные силы (рис. 2.21)

Отделим участок длиной х и заменим левую часть на действие соответствующей системы сил

F+ Q= 0; F(l-x)- M_ux= 0. (2-105)

Здесь Q - перерезывающая сила; M_ux - изгибающий момент в конкретном сечении балки, расположенном на расстоянии х от начала координат. Видно, что перерезывающая сила постоянна по всей длине балки и равна Q= -F, а изгибающий момент меняется по длине M_ux= = F(l-x).

Следовательно, в сечениях балки кроме нормальных напряжений s, действуют и касательные напряжения t.

Из-за сложности фактической картины действия различных напряжений приняты основные допущения:

1. В балке существует нейтральная ось такая, что каждый элемент балки на ней только изгибается, но не удлиняется и не укорачивается.

2. Плоские сечения, перпендикулярные к нейтральной оси в начальном недеформированном состоянии, после изгиба остаются плоскими и перпендикулярными к изогнутой нейтральной оси.

Эти допущения позволяют вывести закон распределения нормальных напряжений в любом сечении балки.

Рассмотрим участок изгибаемой балки (рис.2.22) выше нейтральной оси. Здесь S- длина участка до деформации; S+ DS- после деформации.

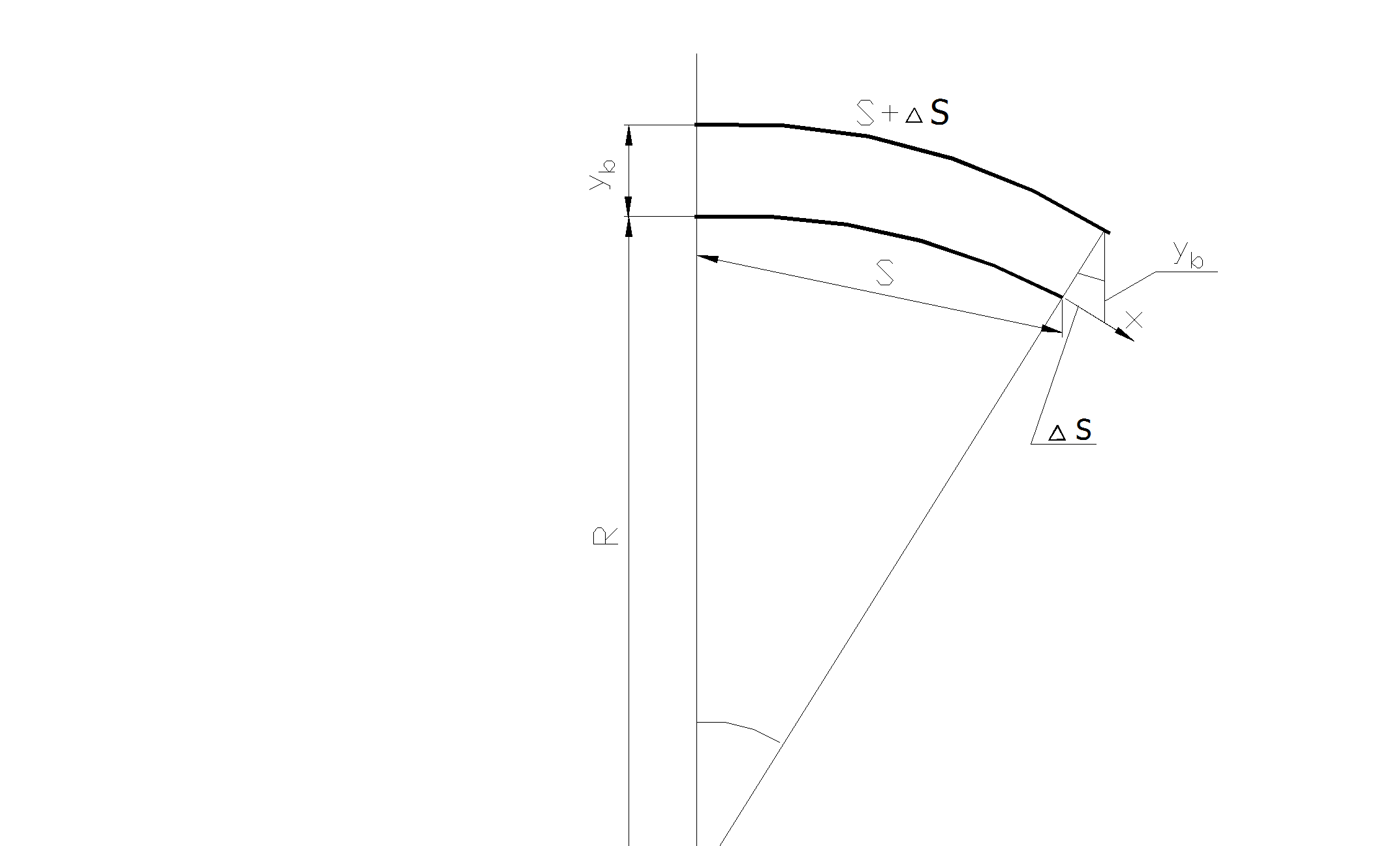
Рис. 2.22

Вывод закона распределения

нормальных напряжений

Относительное удлинение участка будет

e=DS/S. (2-106)

Если рассматриваемое волокно находится на расстоянии y_в от оси х, то из подобия по углам треугольников следует

DS/y_в = S/R или DS/ S= y_в /R.

Тогда с учетом (2-106) нормальные напряжения в сечении будут

s_х= eE= - Ey_в/R. (2-107)

Здесь знак зависит от направления отсчета.

В этом случае изгибающий момент в сечении на расстоянии х от точки отсчета равен

M_ux= 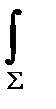(-y_в)s_x df= ER^-1 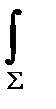y_в²df= ER^-1J_z. (2-108)

Откуда следует R^-1= M_ux/(EJ_z), а учитывая R^-1» d²y/dx², получим

d²y/dx²= M_ux/(EJ_z). (2-109)

Эта формула подобна (2-104), однако здесь изгибающий момент зависит от х. Поэтому изогнутая ось в общем случае не является параболой.

Подставив соотношение для R^-1 в (2-107), получим

s_х= - Ey_в M_ux/(EJ_z)= - y_в M_ux/J_z (2-110)

или максимальные нормальные напряжения при изгибе

½s_{х max}½ = M_ux/W_z, (2-111)

где W_z= J_z / y_в- геометрический момент сопротивления поперечного сечения относительно оси z.

По аналогии с предыдущими случаями потенциальную энергию, накопленную при изгибе можно опредеделить выражением

E_p= 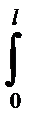[M²_ux/(2EJ_z)]dx. (2-112)