Уравнения движения сплошной cреды.

В теоретической механике в основном имеют дело с сосредоточенными или концентрированными силами, т.е. действующими в точке. В механике сплошной среды рассматриваются распределенные силы, т.е. силы, действующие в каждой части объема V или на каждом элементе поверхности å сплошной среды. Причем при стремлении бесконечно малого элемента объема или поверхности к нулю главный вектор действующих на него сил также стремится к нулю.

Силы, распределенные по объему V, называются объемными или массовыми. Пусть F главный вектор массовых сил, действующих на элемент массы Dm. Тогда плотность массовой силы в данной точке

Á = lim F / m . (2-16)

Dm®0

Для малой частицы F » Á Dm.

Иногда рассматривают силу Ф, приходящуюся не на единицу массы, а на единицу объема

Ф= lim (F /DV) ,

DV ®0

т.е. Ф= r Á. Размерностью произведений ФdV и Ádm является сила; размерностью Á является ускорение, а Ф- ускорение, умноженное на размерность плотности r сплошной среды.

Массовыми силами являются: сила тяжести (вес); гравитационные силы;силы инерции; электромагнитные силы.

В механике абсолютно твердого тела действие любой системы сил эквивалентно действию ее главного вектора и главного момента. В механике деформируемых сред существенен характер распределения сил по телу. Если, например, металлический шток продольно перемещается в среде, плотно его обжимающей по цилиндрической поверхности, то по этой поверхности на шток действуют поверхностные силы. Здесь

p= lim (DP/ Df) - плотность распределения внешних поверхностных сил;

Df®0

DP - изменение суммарной силы, действующей на цилиндрическую поверхность штока; Df - ограниченный участок поверхности штока.

В общем случае внешние поверхностные силы могут действовать не по всей длине тела, а во множестве мест, распределенных случайным образом по длине. Так происходит при бурении нефтяных и газовых скважин, где труба, имеющая меньший наружный диаметр по сравнению с внутренним диаметром поверхности затрубного пространства, под действием разного рода нагрузок изгибается и трется о стенки скважины.

Выделим в сплошной среде тела некоторый произвольный объем V и разобьем его сечением S на две части V₁ и V₂. (рис. 2.2)

Если рассматривать движение одной из частей, например V₁, то действие на нее второй части V₂ необходимо заменить распределенными по V₁ массовыми силами и распределенными по S поверхностными силами.

Сечение S можно проводить по-разному, и тогда распределенные по поверхности S силы будут различаться.

Рис. 2.2

Силы внутренних напряжений

Возьмем некоторую точку М внутри тела и рассмотрим в ней различные площадки df. Ориентацию этих площадок будем определять нормалью n к ним, а полную силу, действующую со стороны части среды в объеме V₂ на часть среды в объеме V₁ на площадки df с нормалью n обозначим через d P. Далее примем d P= = s _n d f , где s _n - конечный вектор.

Вектор s_n можно рассматривать как поверхностную плотность силы взаимодействия разделенных частей вдоль площадки d f. В общем s _n может зависеть от ориентации площадки d f и других ее геометрических свойств. Направление нормали n будем выбирать всегда так, чтобы она была внешней по отношению к той части среды, на которую действует вводимая сила s_ndf. Так, например, влияние объема V₂ на V₁ будем заменять распределенными силами s_n df, а влияние объема V₁ на V₂ - распределенными силами s_-n df = - s_n df (рис.2.2). Такого рода поверхностные силы можно вводить в любой точке сплошной среды. Это силы внутренних напряжений.

Рис.2.3 Разложение сил внутренних напряжений.

s_ndf= s _nn n df + s_nt t df , где s _nndf - нормальная компонента силы внутреннего напряжения; s_ntdf- касательная или тангенцальная сила (сила внутреннего трения).

Поверхностные силы s _n df могут быть и внешними.

В каждой точке M сплошной среды существует бесконечно много векторов s _n , соответствующих бесконечному набору площадок df, проходящих через эту точку. Однако между ними имеется универсальная, независящая от частных свойств движущейся среды, связьdzpp.ений и ___________________________________________________________________________________________________________________.

Уравнение количества движения (импульса).

Основным динамическим уравнением движения материальной точки является 2-й закон Ньютона F = m a , где a= d u /dt

Так как масса постоянна m= const, то

m d u / dt = d( mu) / dt= F.(2-17)

Произведение mu называется количеством движения точки или импульсом.

Для системы из n материальных точек с массой каждой из них m, движущихся со скоростью v_i можно написать d(m_i u_i)/dt = F_i ,

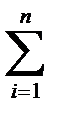d(m_i u_i)/ dt= d ( 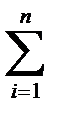m_i u_i)/ dt= 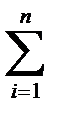F_i ^(e). (2-18)

Здесь справа стоит сумма только внешних по отношению к системе сил, т.к. внутренние силы взаимодействия по 3-му закону Ньютона существуют попарно и при суммировании сокращаются. Выражение (2-18) можно переписать

Q= 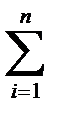m_i u_i= m u^*, (2-19)

где m= 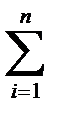m_i - масса всей системы; u ^* - скорость центра масс системы из точек.

Причем u ^*= m^-1 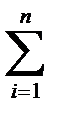m_i u_i

Вектор Q называется количеством движения системы. Тогда уравнение количества движения для системы из n материальных точек можно записать в форме

dQ/ dt= 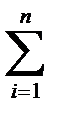F_i^(e) или m d u ^*/ dt= 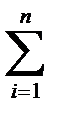F_i^(e). (2-20)

Производная по времени от количества движения системы материальных точек равняется сумме всех действующих на систему внешних сил.

Для конечного индивидуального объема V сплошной среды, ограниченного поверхностью S , напишем уравнение количества движения

dQ/ dt= 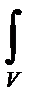Frdd + 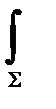s_ndf, (2-21)

где Q= 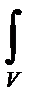u rdd (dd- элементарный объем); 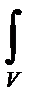Frdd - сумма внешних массовых сил и 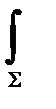s_ndf - сумма поверхностных сил, действующих на среду в объеме V, соответственно.

Следовательно, для любого индивидуального объема V сплошной среды можно записать уравнение количества движения

d ( 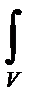urdd)/ dt= 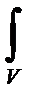Frdd + 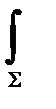s_ndf. (2-22)

Если на массу в объеме V дополнительно действуют еще внешние сосредоточенные в точке силы или силы, сосредоточенные вдоль некоторых линий, то их сумму надо добавить в правую часть (2-22).

С учетом теоремы Гаусса- Остроградского уравнение (2-22) можно переписать в дифференциальной форме при r= const [2]

r d u / dt= Fr + ¶ s₁ /¶ x+ ¶s₂ / ¶ y+ ¶ s₃ / ¶ z , (2-23)

где s₁ , s₂ , s₃ - напряжения, направленные параллельно координатным плоскостям прямоугольной декартовой системы координат.

Уравнение моментов количества движения

Умножив уравнение mdu/dt= Fвекторно слева на радиус вектор рассматриваемой точки массой m относительно некоторой точки О- начала инерционной системы координат, получим уравнение моментов количества движения для точки

dK/ dt= Ф, (2-24)

где K= rx mu; Ф = r x F.

Для массы n материальных точек с массами m_i , движущимися со скоростями u_i , можно написать

d(r_i x m_i u_i)= r_i x F_i ,

где F_i - главный вектор всех, в том числе и внутренних сил по отношению ко всей системе сил, действующих на рассматриваемую точку с массой m_i.

В сумме для K= 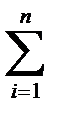(r_ix m u_i) получим

dK / dt= 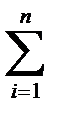(r_ix F_i ^(e)). (2-25)

Здесь справа в силу 3-го закона Ньютона стоит сумма моментов только внешних для всей системы сил.

Следует отметить, что момент количества движения системы материальных точек можно записать в форме

K= r^* x mu^*+ (r_{i отн}х mu_{i отн}) , (2-26)

где m= 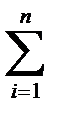m_i ; r^*, u^*- радиус- вектор и скорость движения центра масс; r_{i отн} , u_{i отн} - радиус- вектор и скорость движения i-й точки относительно центра масс и движущейся вместе с центром масс.

Моментом количества движения конечного объема V сплошной среды обычно называют [2]

K= 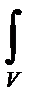r xur dd , (2-27) где r - радиусы- векторы точек сплошной среды относительно некоторой неподвижной точки O, а u - их скорости.

Если скорость объема d сплошной среды u= u^*+ u _отн , где u^* - скорость рассматриваемой точки относительно центра масс, то можно записать

K=r x Q+ 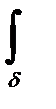r_отн х u_отн r dd ,

где Q= m u^*- количество движения материальной точки массы m, совпадающей с центром масс.

Возможна также запись K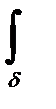^*= r_отн х u_отн r dd .

Момент количества движения равен [2]

K= 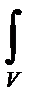r xur dd + 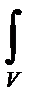k r dd, (2-28)

где k - плотность собственных или внутренних моментов количества движения.

С учетом изложенного, уравнение моментов количества движения системы материальных точек конечного индивидуального объема V сплошной среды можно записать в форме

d( 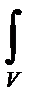r xur dd + 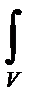k r dd)/dt=

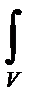= r xаr dd + 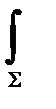rx s_ndf + 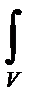hrdd+ 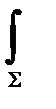q_ndf. (2-29)

Производная по времени от момента количества движения произвольного индивидуального объема V сплошной среды (с учетом собственных моментов) равна сумме моментов внешних массовых и поверхностных сил, действующих на этот объем, и сумме моментов, действующих на этот объем распределенных массовых и поверхностных пар, вызванных внешними по отношению к объему материальными объектами. Здесь вектором а обозначено ускорение от массовых сил, например ускорение свободного падения.

Уравнения (2-22) и (2-29) являются базисными векторными уравнениями, и они применяются для любых сплошных сред и любых движений.

В классическом случае уравнение (2-29) при отсутствии внутренних моментов количества движения и распределенных массовых и поверхностных пар имеет вид

d( 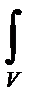r xur dd)/dt= 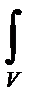r xаr dd + 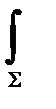А df, (2-30)

где А=r x s_n

В случае непрерывных движений сплошной среды можно, воспользовавшись равенством А= А₁ cos (n, x)+ А₂ cos(n, y)+ А₃ cos(n, z) и теоремой Гаусса- Остроградского, получить

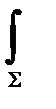Аdf= 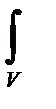divА dd .

Моменты распределенных поверхностных пар можно представить в виде Q_n= Q_in_i .

Тогда с помощью теоремы Гаусса- Остроградского 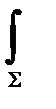Q_ndf= 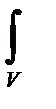div Qdd .

Полагая dm= rdd= const, уравнение (2-29) перепишем

d 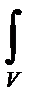(rxur +kr dd)/dt= 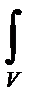r xаr dd + 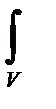[divА + div Q] dd + 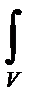hrdd .

Откуда в дифференциальной форме

rd (r xu +k)/dt= r r xа + divА + div Q + hr . (2-31)

Так, для вращающегося относительно своей оси с угловой скоростью W стержня при отсутствии массовых сил (а=0), распределенных массовых (h=0) и поверхностных пар (Q=0) дифференциальное уравнение момента количества движения запишется r¶ (r²W) / ¶ t= ¶(rt)/ ¶x.

Здесь k= r²W ;¶ А/¶ х= ¶(rt)/¶х; t - касательные напряжения по сечению стержня.

Если рассматривать максимальные касательные напряжения на наружной цилиндрической поверхности радиусом r_o и учитывать, что возникающие напряжения направлены в противоположную от скорости движения сторону, то это уравнение можно переписать в форме

r_or ¶ W / ¶ t= - ¶ t_max / ¶ x. (2-32)

Положим теперь, что на стержень действуют какие-либо внешние объекты, приводящие к появлению распределенных поверхностных пар.

Тогда можно записать r¶ (r²W)/ ¶ t= ¶(rt)/ ¶x + ¶ Q / ¶x.

Пусть при вращении на индивидуальный объем среды действует сила трения, создающая, момент h=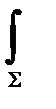rх vhdf , где v- скорость скольжения поверхности стержня относительно контактирующей поверхности; h - коэффициент трения.

Из теоремы Гаусса- Остроградского следует

h=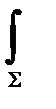rх vhdf= 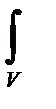div (rх vh)dd

Так как это взаимодействие происходит только по поверхности, то r= r_o. В связи с чем ¶ Q / ¶x= ¶ (r²_oW h)/ ¶x.

Из последнего равенства следует, если h= const, то ¶ Q / ¶ x = 0. Обычно коэффициент потерь на трение является функцией скорости скольжения, необязательно линейной. Связь с длиной стержня может быть и есть, например, при проводке скважин, но весьма неоднозначная.

2.4. Линейное упругое тело.

Линейное упругое тело является частной моделью сплошного тела.

Упругим телом, по Седову [2], называется среда, в которой компоненты тензора напряжений в каждой частице являются функциями компонент тензора деформаций, компонент метрического тензора, температуры и, возможно, других параметров физико-химической природы (например, концентрации фаз).

Уравнения движения в перемещениях, уравнения Ламе, имеют вид

(l+ m) grad (div w) + mDw+ rF= ra (2-33)

или в декартовой системе координат

ra_x= (l+ m) ¶(¶ w₁ /¶ x+ ¶ w₂ /¶ y+ ¶ w₃ /¶ z)/ ¶ x+

+ m (¶ ²w₁/¶ x²+ ¶ ²w₁/¶ y²+ ¶ ²w₁/¶ z²)+ rF_x ,

ra_y= (l+ m) ¶(¶ w₁ /¶ x+ ¶ w₂ /¶ y+ ¶ w₃ /¶ z)/ ¶ y+

+ m (¶ ²w₂/¶ x²+ ¶ ²w₂/¶ y²+ ¶ ²w₂/¶ z²)+ rF_y ,

ra_z= (l+ m) ¶(¶ w₁ /¶ x+ ¶ w₂ /¶ y+ ¶ w₃ /¶ z)/ ¶ z+

+ m(¶ ²w₃ /¶x ²+¶ ²w₃ /¶ y ²+ ¶ ²w₃ /¶ z²)+ rF_z ,

где w₁, w₂, w₃ - компоненты вектора перемещения w; a - вектор ускорения.

Вместо коэффициентов Ламе l и m в теории упругости введены модуль Юнга (модуль упругости)

E= m(3l+ 2m)/ (l+ m) (2-34)

и коэффициент Пуассона, характеризующий сужение поперечного сечения.

c= l/[2(l+ m)]. (2-35)

Эти коэффициенты можно также определить из выражений

c=Drl/(rD l); E= Ds l/D l,

где D r, D l, Ds- соответственно, отклонения радиуса сечения, длины участка, напряжения.

После упрощения уравнения Ламе записываются в форме

(¶ ²a/¶ t ²)_xi = F+ (l+ m)r ^-1_o grad (div w) + m r ^-1_oD w. (2-36)

При наличии движения температура в упругом теле, вообще говоря, не остается постоянной, а меняется как с течением времени, так и от точки к точке объема, занятого упругим телом.

Однако в случае волновых процессов, распространяющихся в упругом теле, температура из-за ее малой скорости изменения может считаться постоянной, т.е. процесс будет адиабатическим.

В этой связи, полагая массовые силы равными нулю F= 0, для компонент вектора перемещения w из уравнения (2-36) выводятся уравнения [2]

¶ ² w₁/¶ x ²= a^-2₁¶ ²w₁/¶ t ², (2-37)

¶ ² w₂ /¶ x ²= a^-2₂ ¶ ²w₂ /¶ t ², (2-38)

¶ ² w₃ /¶ x ²= a^-2₂ ¶ ²w₂ /¶ t ², (2-39)

где a₁= [(l_а +2m_а)/ r]^1/2- скорость распространения продольной волны возмущений; a₂= (m_а/r)^1/2- скорость распространения поперечной волны возмущения.

Здесь указаны значения коэффициентов Ламе для адиабатических процессов. В случае изотермических процессов в качестве нижнего индекса станет применяться буква «и». Когда не учитываются термодинамические особенности, то индексы не будут применяться.

Следовательно, плоская упругая волна представляет собой две независимо распространяющиеся волны. В одной смещение w₁ совпадает с направлением распространения самой волны. В другой - смещение лежит в плоскости, ортогональной к ее направлению, т.е. существуют две скорости звука. Например, для железа a₁ = 7000 м/с, а₂ = 3200 м/с. Поперечная волна сопровождается вращением частиц среды, но в ней не происходит изменения их объема. В продольной- наоборот, изменяется объем частиц, но нет вращения.

Скорость продольных волн в изотропной твердой среде в справочнике по физике Яворского В.М., Детлафа А.А. описывается также выражением

a₁= [Er ^-1(1- c) (1+c)^-1 (1- 2c)^-1]^1/2=q (Er ^-1)^1/2, (2-40)

а поперечных

a₂=(G/ r)^1/2 , (2-41)

где G= E/[2(1+c)] - модуль сдвига; q= [1- 2c²/(1-c)]^-1/2.

Для стали модуль упругости (продольной упругости) равен Е@ @2,1*10⁵МПа, коэффициент Пуассона - c= 0,24- 0,28; модуль сдвига G@ 8*10⁴МПа. Тогда из (2-40) получим

а₁» 1,106(Е /r)^1/2.

Если полагать плотность, коэффициенты Ламе постоянными для данного материала, то, экспериментально определив скорость распространения звуковой волны, величину модуля упругости можно вычислить из выражения

E= a²₁r/q ². (2-42)

Использованные выше коэффициенты в общем случае зависят от многих факторов. Поэтому при точных расчетах необходимо учитывать переменность указанных величин.

При растяжении (сжатии) упругую деформацию металла в машинострои-тельной практике описывают законом Гука s= Ee. Здесь e = D l/l-относительное удлинение.

Вообще, вопросами передачи энергии через металлические детали занимается также реология. До настоящего времени при традиционном подходе в этом процессе весьма много неясностей. Существует ряд гипотез и соответствующих феноменологических моделей Максвелла, Фойгта, Зинера.

Так, из часто применяемой при анализе модели Зинера следует, что передачу движения через элементарную частицу вещества можно описать общим уравнением

s+ t_e ds/dt = Е₁(q+t_s dq/dt),(2-43)

где Е₁ - модуль упругости при изотермическом процессе депформации; t_e2- время релаксации при условии постоянной деформации; t_s - время ретардации (запаздывания); q- деформация.

Реологические исследования дали основание ввести дополнение к закону Гука, учитывающее особенности передачи динамических воздействий и записываемое в преобразованиях по Лапласу (см. подробнее гл.3) следующим образом:

Е_w= s(jw)/ q(jw)= E_u + jE, (2-44)

где w - частота колебаний.

Это уравнение позволяет представить процесс прохождения гармонического сигнала в виде частотной характеристики, показанной на рис. 2.4

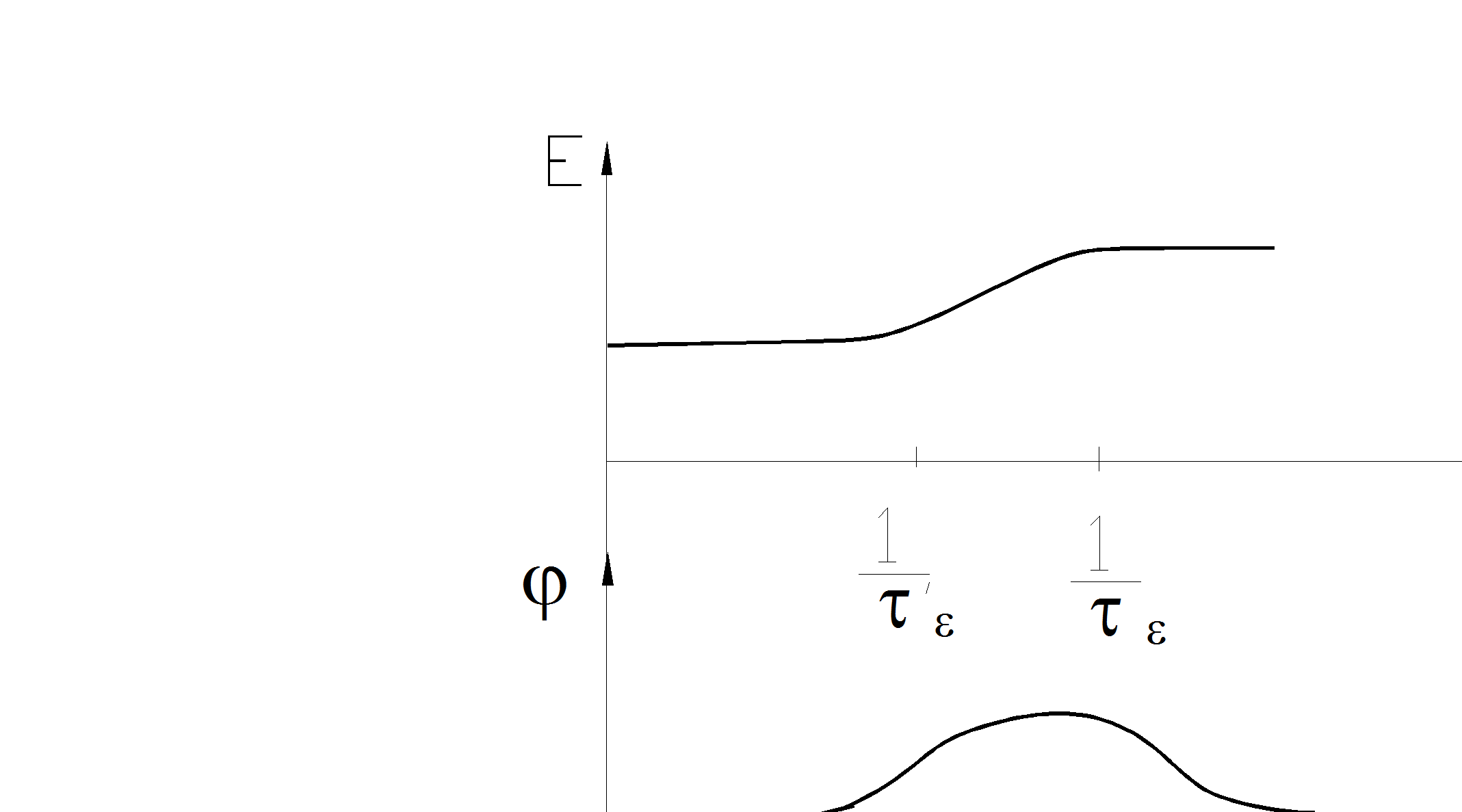
Рис. 2.4

Особенность прохождения гармонического сигнала через металл (t’_e = t_eE₂/E₁; E₂ - модуль упругости при адиабатической деформации; j - сдвиг по фазе).

Измеряя скорость распространения звуковых волн, коэффициент затухания и учитывая значение q (см.(2-40)) , можноопределить Е_w. Кроме того, для процесса передачи мощности характерна нелинейная зависимость- гистерезисная петля, показанная на рис.2.5 .

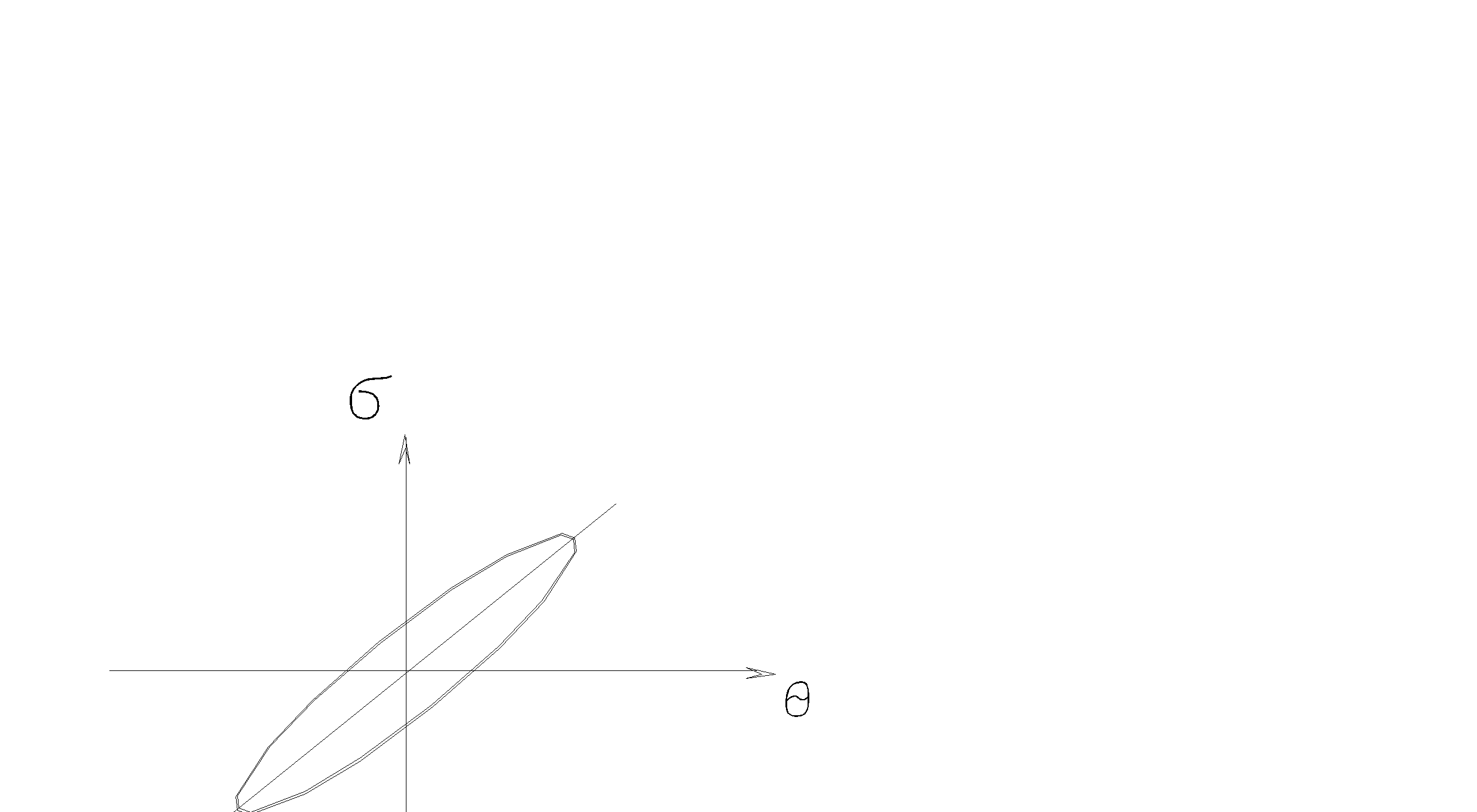
Рис.2. 5.

Гистерезисная петля.

Если обратиться к кристаллам, то закон упругой деформации может быть выведен из рассмотрения упругого взаимодействия атомов. Взаимосвязь сил отталкивания и притяжения имеет такой же характер, как и при взаимодействии ионов и электронов в атоме рис.2.6.

На больших расстояниях а притяжение и отталкивание пренебрежительно малы, но при сближении они возрастают. При таком выводе следует, что в зоне больших упругих деформаций или больших напряжений закон Гука становится нелинейным. Об этом свидетельствует и форма гистерезисной петли.

В случае скручивания закон Гука записывается в форме t = GJ- для малых деформаций. Здесь t- максимальное касательное (скалывающее) напряжение; G- модуль сдвига (для стали G= 8*10⁴ МПа); J- угол сдвига (поворота) в радианах. Полный поворот сечения на расстоянии z от начала координат равен j=J‘z, где J‘= =dj /dz- относительный угол закручивания.

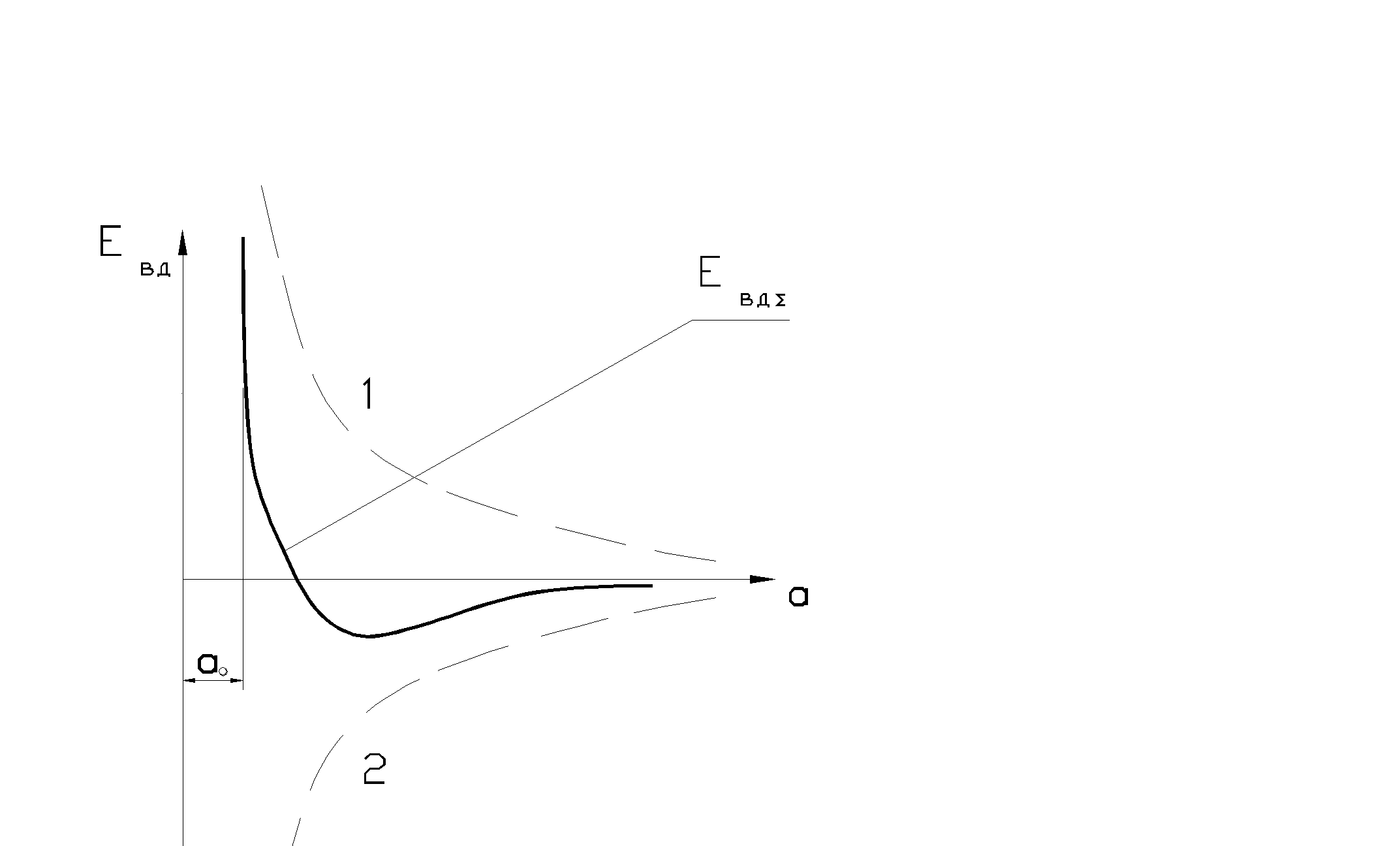
Рис. 2.6. Зависимость энергии взаимодействия Е_вд между ионами и электронами в кристалле: 1- силы отталкивания; 2- силы притяжения; Е_вдå- суммарная энергия взаимодействия.

Модули упругости определяют статическими и динамическими методами.

Статические. Под действием нагрузки происходит растяжение, измеряя которое, определяют модуль упругости E.

Недостаток заключается в том, что для получения точного результата нужна большая деформация, но при этом есть вероятность пластической деформации.

Динамические. Модуль сдвига G определяют по частоте крутильных колебаний. Модуль упругости E определяют по частоте изгибных колебаний.

Импульсный метод основан на определении скорости распространения волн через образец.

При всестороннем сжатии

s= KDV/ V, (2-45)

где К- модуль всесторонней объемной упругости; DV - изменение объема.

Приближенно DV/ V @ 3 Dl/ l= 3s / E, т.е. s/К= 3s/Е. Откуда К= Е/ 3.

В практике машиностроения обычно полагают E= const, G= const.

С учетом изложенного, с достаточной для практических расчетов точностью уравнение продольных колебаний можно записать в форме

¶ ²u / ¶ t ²= (E/r)¶ ²u /¶ x², (2-46)

где u - перемещение вдоль оси.

При скручивании вала, стержня происходит последовательный поворот множества плоских поперечных сечений на расстоянии по оси друг от друга dx. Причем, как показывает теория упругости [2], эти сечения практичеси поворачиваются как твердые диски. Следовательно, точки двух сечений находящиеся на расстоянии r_i от оси при повороте сечения на угол dj смещаются друг относительно друга на расстояние

dw₂= r_idj. (2-47)

Поэтому в случае отсутствия продольных колебаний и при действии только скручивающего импульса в стержне возникнут скручивающие движения, когда каждая точка от близлежащей будет смещаться на расстояние dw₂. Подставим (2-47) в уравнение (2- 38) и сократим на r_i

¶ ²j / ¶ t ²= (G /r)¶ ²j /¶ x². (2- 48)

Основные понятия теории сопротивления материалов.

Ниже рассматриваемые основные понятия теории сопротивления материалов (сопромата) базируются на положениях механики сплошных сред, приведенных в разделах 2.1- 2.4, из-за чего возможны повторения.

Если на стержень, площадь сечения которого равна f, в осевом направлении действует сила F, то в теле стержня образуются продольные напряжения

s= F/f. (2-49)

Из простых экспериментов получено, что под действием силы F происходит продольная деформация. При этом удлинение равно

Dl= Fl/(Ef)= JF, (2- 50)

где J= l/(Ef)- коэффициент продольной упругости.

Из этой формулы можно также определить относительное удлинение e = Dl /l = s / Е и закон, называемый законом Гука,

s = Еe. (2-51)

Если стержень имеет переменное сечение, то его удлинение будет

Dl= 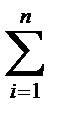F_il_i/(E_if_i),

где индекс i относится к каждому участку.