Теорема Гаусса - Остроградского.

Рассмотрим в движущейся среде в момент времени t индивидуальный объем V сплошной среды, ограниченный поверхностью å. В каждой точке этой поверхности выберем внешнюю по отношению к V нормаль n . В момент времени t + Dt этот объем перейдет в объем V¢, а å - в поверхность å¢, ограничивающую V¢.

Изменение объема V¢- V= 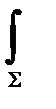_nDtds, где _n - проекция скорости uна нормаль n; ds - элементарная площадь поверхности å.

Уменьшение V¢ по отношению к V учитывается условием, что нормаль всегда внешняя к V. Скорость изменения объема равна

lim (V¢-V 0)/ Dt Dt®0

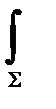
= _n ds (2-13)

Рис. 2.1.

К теореме Гаусса- Остроградского.

В том числе для бесконечно малого объема V^*, ограниченного поверхностью å^*

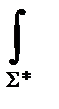
_n ds

Из определения дивергенции следует

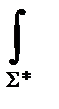
_n ds= 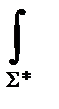[ucos(n, x)+ v cos (n, y) + w cos(n, z)] d s =

= V^*div 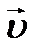+ V^*e= (¶ u/ ¶x+ ¶ v/¶y+ ¶ w/¶ z)dt, (2-14)

где t - элементарный объем.

Здесь находящиеся в левой части интегралы, взятые по смежным поверхностям å^*, в силу противоположных направлений нормалей к ним сократятся и в пределе останется только интеграл по внешней поверхности å.

Выражение (2-14) представляет собой теорему Гаусса-Остроградского о преобразовании интеграла, взятого по замкнутой поверхности å, в интеграл, взятый по ограниченному этой поверхностью å объему V.

Уравнение (2-14) можно переписать в виде, независимом от выбора системы координат

_n ds = 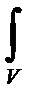div u dt. (2-15)