Надежность и ее оценка

Надежность слагается из безотказности, ремонтопригодности, долговечности и сохраняемости изделия [1].

В зависимости от вида устройства надежность может определяться разными параметрами. Так, надежность подшипника определяется его долговечностью; зубчатого колеса- безотказностью, долговечностью, ремонтопригодностью.

Безотказность- это свойство изделия сохранять непрерывную работоспособность;

долговечность- свойство сохранять работоспособность до предельного состояния с необходимыми перерывами для технического обслуживания и ремонтов;

ремонтопригодность- это свойство изделия, позволяющее производить его ремонт и техническое обслуживание;

сохраняемость- это свойство изделия сохранять показатели качества в течение срока хранения и транспортирования, а также после них.

Показатели безотказности различают для невосстанавливаемых и восстанавливаемых изделий. Для невосстанавливаемых изделий понятия надежность и долговечность совпадают. Для восстанавливаемых- безотказность это одно из свойств, определяющих их надежность.

Показателями безотказности невосстанавливаемых изделий являются- вероятность безотказной работы, средняя наработка на отказ, интенсивность отказов; для восстанавливаемых изделий- вероятность безотказной работы, наработка на отказ, характеристика и параметр потока отказов.

Расчеты приведенных показателей проводятся на базе теории вероятностей.

Для определения показателей безотказности невосстанавливаемых изделий необходимо знать распределение отказов, как случайных величин.

Распределение описывается характеристиками плотности распределения отказов f(x), интегральной функцией распределения отказов Q(x) и вероятностью безотказной работы Р(х). Существует зависимость

f(x)= dO(x)/dx. (1-4)

Отсюда произведение f(x)Dx при достаточно малом Dx приблизительно равно вероятности нахождения х в интервале [x_i , x_i + Dx] При наработке х, не превышающей требуемой x_i , с помощью плотности распределения получаем

P(x£ x₁)= 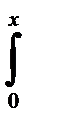f(x)dx, (1-5)

где x- переменная интегрирования.

Вероятность безотказной работы Р(х) определяется из плотности распределения отказов. Так как в рассматриваемом случае изделие может быть в состоянии отказа или работоспособности, то P(x₁)+ Q(x₁)=1. Отсюда

P(x₁)= P(x> x₁)= 1 – Q(x₁)= 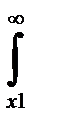f(x) dx. (1-6)

Плотность распределения отказов позволяет найти вероятность того, что случайная величина x заключена между х₁ и х₂.

Среднюю наработку на отказ можно определить из выражения

x_cp= 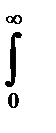xf(x) dx. (1-7)

или посредством приближенного вычисления

`х_ср= ( x_i)/N, (1- 8)

где N- число испытуемых изделий; x_i - суммарная наработка испытуемых изделий до отказа.

Если из N наблюдаемых изделий за время Т отказало r изделий, то средняя наработка до отказа будет

`х_ср=[ x_i +T(N- r)]/r. (1-9)

Условие отсутствия отказов до рассматриваемого момента времени может быть выражено интенсивностью отказов

l(x)= f(x)/P(x). (1-10)

Рис. 1.3

Изменение интенсивности отказов в зависимости от наработки.

На рис. 1.3 приведен распространенный вид функции интенсивности отказов. Здесь наработка распределена на 3 периода. Период I относится к приработке изделия, когда интенсивность отказов повышена. Период II называется периодом нормальной эксплуатации, когда интенсивность отказов является минимальной и интенсивность отказов постоянна по величине. В периоде III начинают проявляться отказы из-за интенсивности износа, усталостных разрушений, старения и других причин, обусловленных длительностью эксплуатации.

Вероятность безотказной работы равна

P(x)= exp[- l(x)dx]. (1-11)

Долговечность изделия оценивается по ресурсу (наработке) и сроку службы (продолжительности эксплуатации). Если ресурс дает непосредственное представление о наработке в различных условиях, то срок службы удобен для планирования сроков сдачи изделий в ремонт, замене их новыми и т.д.

Показатели ремонтопригодности зависят от процессов восстановления, технического обслуживания и ремонта.

1. 4. Условия работы машины и причины отказов.

В одних типах устройств в широких пределах меняется режим работы, в других- режимы меняются циклично. В результате отказы различных элементов образуют случайный поток событий.

В основе всей теории надежности лежат сведения об отказах. Эти сведения могут быть даны в эмпирической или аналитической формах.

Если после испытаний получена информация об отказах, то методами математической статистики можно найти по этим данным статистическую модель, описывающую явление. Может быть и обратная задача, когда задается статистическая модель, а по ней определяются характеристики надежности системы.

Существуют разные подобные характеристики.

Наиболее часто используется нормальное распределение (Гауссово).

Выражение плотности нормального распределения записывается в форме

f(x, m,s)= [s(2p)^1/2 ]^-1exp{-(x- m_[)²/(2s)}; (1-12)

0<x<µ ; 0< m_x < µ ; s> 0.

Здесь m_x - среднее значение или математическое ожидание (параметр, характеризующий центр распределения); s- средне- квадратическое отклонение случайной величины x (параметр, характеризующий масштаб распределения). Поэтому x_cp= m_x.

Кривая, иллюстрирующая эту функцию, приведена на рис 1.4.

Исходными данными для определения распределения служат наблюдаемые значения случайной величины, сгруппированные в интервалы, по которым строится гистограмма или график плотности распределения. По этим графикам, в ряде случаев с помощью ЭВМ, находится закон распределения случайной величины. Часто пользуются приближенными рекомендациями.

Рис. 1.4

Плотность нормального распределения

Нормальное распределение обладает тем свойством, что композиция случайных ве-личин с нормальным законом распределения есть тоже нормальное распределение.

Экспоненциальное распределение служит распространенной статистической моделью для времени безотказной работы. Оно предполагает, что отказы происходят независимо друг от друга с постоянной интенсивностью.

Важно только, чтобы каждый элемент в отдельности не оказывал очень большого влияние на вероятность выхода из строя всей системы. Это распределение часто описывает распределение времени безотказной работы систем, в которых каждый отказавший элемент немедленно заменяется работоспособным.

Выражение, характеризующее плотность распределения отказов имеет вид

lexp(-lx);

f(x, l)= x³ 0; l³ 0; (1-13)

0 в остальных случаях .

Экспоненциальное распределение зависит от одного параметра l.

Если имеется наработка x₀, в течение которой отказы не поступают, то

lexp[-l(x- x₀)];

f(x, l)= x³ 0; l³ 0 (1-14)

0 в остальных случаях .

Средняя наработка до отказа (математическое ожидание) x_cp=l^-1.

Распределение Вейбулла соответствует более общей статистической модели, охватывая различные законы изменения случайной величины с течением времени. Плотность распределения

ba^-1(x/a)^b-1 lexp[- (x/a)^b ];

f(x,a, b)= x³ 0; a³ 0; b³ 0; (1-15)

0 в остальных случаях .

Распределение Вейбулла – двухпараметрическое. Параметр а называют иногда параметром масштаба, а параметр b- параметром формы.

Экспоненциальное распределение- это частный случай распределения Вейбулла.

1.5. Надежность машин при проектировании и эксплуатации.