Мощности.
2. 1. Основные положения механики сплошных сред [2].
Известно, что все тела представляют собой совокупность разнообразных молекул и атомов, определенным образом организованных в тех или иных материалах.
В металлах они объединены в кристаллы- твердые тела, имеющие правильное периодическое расположение составляющих их частиц, ограниченные плоскими, упорядочено расположенными друг относительно друга гранями, сходящимися в ребрах и вершинах. Кристаллы могут объединяться в кристаллиты. В сплавах возникают разные фазы, зерна и т.п.
Для кристалла характерна анизотропия свойств по разным направлениям. Однако в случае содержащихся разнонаправленных кристаллов может возникнуть такое явление, как квазитропия, т.е. по всем направлениям свойства будут одинаковыми.
В неметаллах элементарные частицы вещества объединены в молекулы разных форм: цеповидные, разветвленные, плоские и др.
Кроме того, в металлах, сплавах, сначала имеющих квазитропию, после мехобработки (прокатки) может возникнуть анизотропия, обусловленная появлением соответствующих слоев и т.п. Это существенно изменяет свойства материалов.
В конечном итоге взаимодействия в материале могут быть приведены к электромагнитным силам, которые в кристаллах металла имеют одну величину, а на стыке зерен- другую, существенно меньшую.
В расчетах в принципе можно отслеживать движение весьма малых участков деформируемого тела. Для этого необходимо использовать соответствующий математический аппарат и мощные электронные вычислительные машины (ЭВМ). Тогда появляется возможность учета выше отмеченных особенностей.
1Рассматривая далее среду, как сплошную, состоящую из отдельных частиц, может быть достаточно крупных, но являющуюся квазитропной, опишем некоторые основные ее свойства.
Под пространством будем понимать совокупность точек, задаваемых числами- координатами. При этом будем рассматривать 3-х мерные пространства, где расстояния между двумя точками определяется по формуле
r= [(x1- x2)2+ (y1- y2)2+ (z1- z2)2]1/2, где x1, x2 , y1, y2,, z1, z2- координаты точек.
Если следовать общей теории относительности, то время t зависит от скорости перемещения. Такой, новый подход к описанию процессов в твердых телах, учитывающий этот фактор, впервые изложен в статье Чернышева Г.Н., Иванова С.Д.2, где введена в рассмотрение четырехмерная модель упругого тела. В предлагаемой же книге, используя традиционные представления Лагранжа при недеформируемом времени, будем полагать, что точка с координатами x1, x2, x3 (x1= x; x2= y; x3= z) движется, если ее координаты меняются со временем
xi= fi(t) (i= 1, 2, 3). (2-1)
Сплошная среда представляет собой непрерывную совокупность точек (частиц) - континуум. Знать движение среды - это значит знать движение всех ее частиц.
Для любой точки континуума, выделяемой координатами а, b, c, можно написать закон движения или перемещения, куда входят функции 4-х переменных 
x1= x1(a, b, c, t), x2= x2 (a, b, c, t), x3= x3(a, b, c, t) или
xi= xi(a, b, c, t), i=1, 2, 3. (2-2)
Если в функциях (2-2) a, b, c фиксированы, а t= Var, то (2-2) описывает движение одной фиксированной точки. При a=Var, b= Var, c= Var, t= const функ-ции (2-2) дают распределение точек континуума в данный момент времени.
Если переменными будут a, b, c, t, то функции (2-2) описывают движение сплошной среды и являются законом движения континуума.
Координаты a, b, c или z1, z2, z3 , индивидуализирующие точки континуума, и время t называются переменными Лагранжа.
Обычно основной задачей механики, по крайней мере, применительно к твердым телам, считалось определение функций (2-2). Однако в ряде случаев возникает необходимость изучения закона не перемещения, а скоростей движения континуума и напряжений, возникающих при этом.
Причина заключается в том, что существуют механические системы, например приводы, где более важно знать изменения скоростей и напряжений. Поэтому для них изучение закона перемещения является избыточным, поскольку приводит к необходимости дополнительных исследований, например форм колебаний.
Учитывая физический опыт, предположим, что в каждый фиксированный момент времени t= const функции xi= xi(a, b, c, t) являются взаимнооднозначными функциями. В этом случае якобиан
¶x1/¶z1 ¶x1/¶z2 ¶x1/¶z3
D = ¶x2/¶z1 ¶x2/¶z2 ¶x2/¶z3
¶x3/¶z1 ¶x3/¶z2 ¶x3/¶z3
не может обращаться в нуль во всех точках некоторого конечного объема. Если D ¹ 0, то формулы (2-2) можно разрешить относительно z1, z2 , z3 и представить решение в виде однозначных непрерывных функций
zi= zi (x1, x2, x3,, t).(2-3)
Совокупность значений x1, x2, x3 образует в пространстве область D, занимаемую телом в данный момент времени t. Если координаты z1, z2 , z3 рассматривать как значения координат x1, x2, x3 в некоторый другой момент времени t0 , то область D0 изменений z1, z2 , z3 соответствует объему, занятому телом в момент времени t0.
В этом случае законы движения (2-2), (2-3) можно рассматривать как взаимнооднозначное и непрерывное отображение областей D и D0.
Пусть некоторая точка сплошной среды в момент времени t находится в точке М пространства, а в момент t+Dt- в точке М¢. Тогда расстояние ММ¢ = D r. Под Dr , понимается малое направленное перемещение индивидуальной точки сплошной среды за время Dt. В евклидовом пространстве Dr представляет собой приращение радиуса- вектора r, рассматриваемой точки сплошной среды. Здесь и далее векторные величины будем обозначать жирным шрифтом. В некоторых случаях для этого будем использовать букву со стрелкой вверху.
Частная производная ¶ r /¶ t = uназывается скоростью движения точки сплошной среды. Это векторная величина. Поскольку радиус- вектор зависит от z1, z2 , z3 и t, то поэтому и берется частная производная по t.
Скорость вычисляется относительно системы отсчета, которая в общем случае выбирается произвольно и может быть подвижной и неподвижной.
Через каждую точку пространства проходит 3 координатные линии и в каждой точке пространства M(x1, x2, x3) можно рассмотреть элементарные прямолинейные направления D r 1, D r 2, D r 3 , выходящие из этой точки и соединяющие ее с точками М1(х1+Dх1, х2, х3), М2(х1, х2+Dх2, х3), М3 (х1, х2, х3+Dх3) соответственно. В каждой точке пространства можно ввести пределы
lim (D r i /Dxi ), lim (D r i /Dz i ),
Dx® 0 Dz® 0
которые будут направлены по касательным к соответствующим координатным линиям в точке М.В эвклидовом пространстве эти пределы являются частными производными от Dr по соответствующим координатам. Если под Dx i или Dz i понимать длины дуг вдоль соответствующих координатных линий, то ¶ r / ¶ xi , ¶ r / ¶ z i по величине равны единице.
Введем обозначения 
¶ r / ¶ xi = A i и  ¶ r / ¶ z i =
¶ r / ¶ z i = 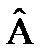 i
i  (2-4)
(2-4)
и будем аналогично [2] называть их векторами базиса системы отсчета и для соответствующей системы соответственно.
Если система координат x1, x2, x3 декартова, то можно пользоваться обозначениями
A 1 = i ; A 2 = j ; A 3= k ,
где i , j , k - единичные векторы по осям координат x, y, z соответственно.
Бесконечно малое перемещение точки сплошной среды ММ¢ = D r можно разложить по векторам базиса A 1, A 2, A 3 , взятым в точке М
Dr = Dх1A 1+ Dх2 A 2+ Dх3 A3 , (2-5)
где Dх1 , Dх2, Dх3 - компоненты перемещения D r.
Разложение (2-5) можно записать в форме D r= 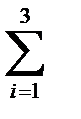 D хi A i .
D хi A i .
Тогда для скорости перемещения можно записать
u = ¶ r / ¶ t= 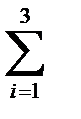
 i A i , (2-6)
i A i , (2-6)
где  i= (¶ x/ ¶ t) z i .
i= (¶ x/ ¶ t) z i .
Переменные  1,
1,  2,
2,  3 называются комплексными векторами скорости u в базисе A 1, A 2, A 3.
3 называются комплексными векторами скорости u в базисе A 1, A 2, A 3.
В декартовой системе координат можно записать
r = x i +y j+ z k , u= u i +v j+ w k, (2-7)
где u= (¶ x/ ¶ t)z i ; v= (¶ y/¶ t)z i ; w= (¶ z/¶ t)z i .
Ускорение описывается выражением
a = ¶ u/ ¶ t= 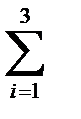 Dai A i
Dai A i  , (2-8)
, (2-8)
где ai= ai(z1, z2 , z3 , t).
В декартовой системе координат верны формулы
a1= ¶ 2x/¶ t 2; a2= ¶ 2y/¶ t 2; a3= ¶ 2z /¶ t 2.
Для твердого тела, совершающего произвольное движение, Эйлером получена формула распределения в нем скоростей движения
u 1= u 0+ W х r, (2-9)
где u 0 - скорость некоторой определенной точки О абсолютно твердого тела; u 1 - скорость любой точки О1 тела; W - вектор мгновенной угловой скорости твердого тела; r - радиус- вектор ОО1.
Рассмотрим понятие дивергенции скорости u .
Возьмем в момент времени t бесконечно малую сферу x2+ y2+ z2= R2, состоящую из точек среды. Через время Dt она перейдет в эллипсоид, уравнение которого будет иметь вид [2]
x*2(1+e1Dt) -2 + y*2(1+e2 Dt) -2 + z*2(1+e3Dt) -2 = R2, (2-10)
где e1 , e2 , e3- главные компоненты тензора скоростей деформаций; x*, y*, z* - главные оси.
В момент времени t объем сферы V0= (4/3)pR3, а в момент t+ Dt -
V= (4/3)pR3(1+e1Dt) (1+e2 Dt) (1+e3Dt).
Тогда предел относительного изменения бесконечно малого объема при t®0, V®0
lim (V-V0)/(V0Dt)= e1+ e2+ e3 . (2-11)
Dt®0
V® 0
Сумма e1+ e2+ e3 - является инвариантной величиной, которая называется дивергенцией вектора скоростей и в декартовой системе координат записывается в форме
div u= ¶ u/ ¶x + ¶ v/¶y + ¶ w/ ¶z . (2-12)
Это изменение не зависит от формы объекта V0 бесконечно малой частицы.
Дата добавления: 2015-02-23; просмотров: 839;
