Пример. 2.1
Определить удлинение болта на рис. 2.7.
D l= FE-1[4l2/(pd22) + 4l1/(pd21)]= 4F(pE)-1(l2d-22+ l1d-21).
В случае одновременного действия сил и температуры деформация может быть определена из выражения
Dl= Fl/(Ef)+ a l (T- T0), (2-52)
где a- коэффициент линейного расширения твердого тела, 1/град; Т, Т0- конечная и начальная температура.
В технике применяются различные схемы нагружения деталей, показанные на рис. 2.7- 2.11.
Если к телу приложено внешнее усилие F, то потенциальная энергия, запасенная телом при деформации, равна
А= FDl/2.
Подставив в это выражение (2-50), получим
А= 0,5FFl/(Ef)= 0,5F2l/(Ef). (2-53)
Разделив эту величину на объем тела, получим удельную потенциальную энергию деформированного тела
Аq= FDl/(2fl)= 0,5s e.. (2-54)
При действии на тело нескольких сил потенциальная энергия равна
А= 0,5 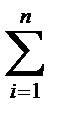 F iDli - формула Клайперона. (2-55)
F iDli - формула Клайперона. (2-55)
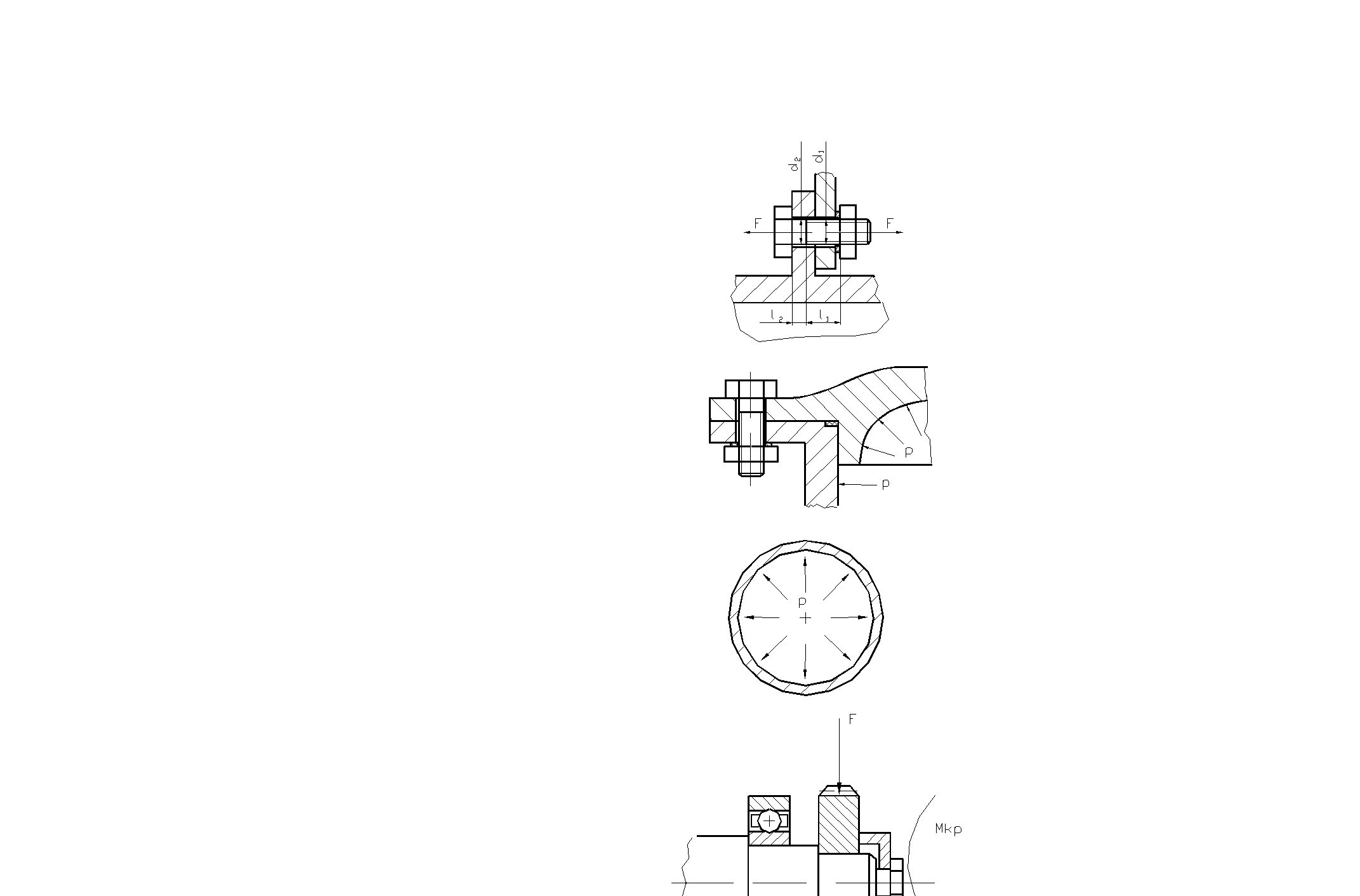
Рис.2.7
Схема сил, действующих на болт.
Рис. 2.8
Схема действия сил на крышке
Рис.2.9
Схема действия сил в трубе
Рис. 2.10
Схема действия сил на вале.
Рис.2.11
Схема действия на стержень нескольких сил
Так, для стержня на рис. 2.11, перемещения точек приложения сил F1 и F2 соответственно равны
Dl1= F1l/(Ef)- F2a/(Ef); Dl2= F1a/(Ef)- F2a/(Ef).
Потенциальная энергия по формуле Клайперона будет
A= 0,5[F21 l/(Ef)- F22a/(Ef)].
Продифференцировав (2-53) по силе, получим
dA/dF= Fl/(Ef)= D l.
Если теперь положить, что на тело действуют несколько независимых сил и потенциальная энергия равна А= 0,5 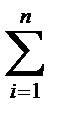 Fi2li/(Eifi) , а слагаемые независимы друг от друга и линейны, то
Fi2li/(Eifi) , а слагаемые независимы друг от друга и линейны, то
¶A/¶Fi = Fili/(Eifi)= Dli .
В этом заключается теорема Кастильяно:
Если на упругое тело, закрепленное на недеформируемом основании, действуют несколько сил, то частная производная от потенциальной энергии тела по какой- либо внешней силе равна перемещению точки приложения этой силы в направлении силы.
Механические свойства конструкционных материалов
|
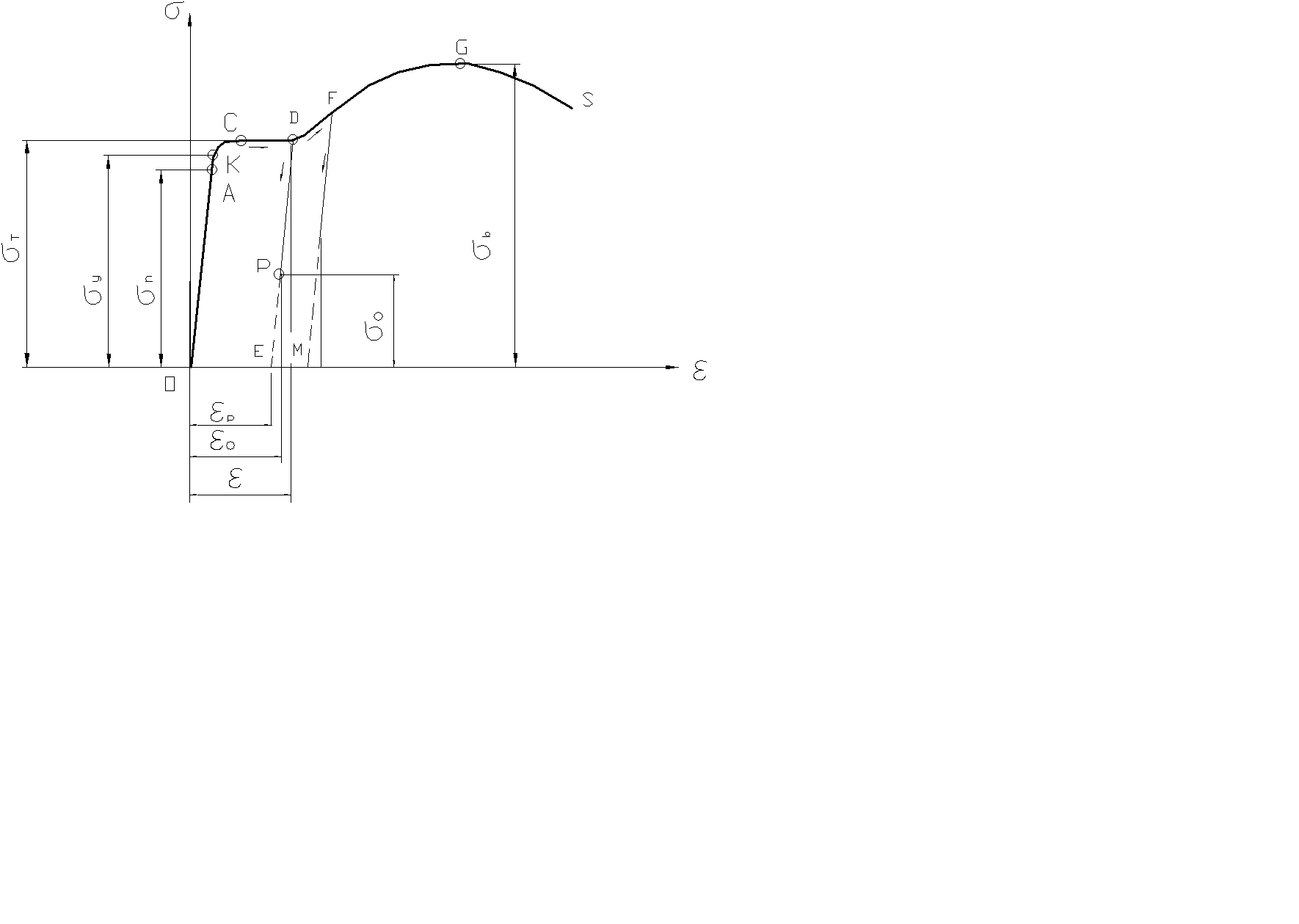
Рис.2.12
Диаграмма растяжения
В расчетах на прочность необходимо знать механические свойства материалов. Часто их определяют по результатам растяжения или сжатия специального образца, которые проводят на универсальных испытательных машинах. При испытаниях обычно определяют диаграммы ратяжения (сжатия) рис. 2.12. Здесь по оси ординат отложено напряжение s, а по оси абцисс- относительная деформация e =Dl/l0 , где Dl - удлинение; l0 - начальная длина рабочей части образца.
Диаграмму можно условно разделить на 4 зоны.
Первая зона называется зоной упругости. Здесь свойства материала на участке ОА подчиняются закону Гука
s= Ee ; F= DlEf0 /l0, (2- 56)
где f0- начальная площадь сечения стержня.
Наибольшее напряжение, до которого материал следует закону Гука, называют пределом пропорциональности sп. Угол наклона прямой ОА a= arctg(s/ e)= arctg E.
Коэффициент Е называют модулем упругости, модулем продольной упругости или модулем Юнга материала.
Напряжение в точке К, называемое пределом упругости sу, позволяет уточнить зону, где возникают остаточные деформации. Обычно sп@ sу .
Вторая зона KD называется зоной общей пластичности. Для нее характерно существенное увеличение деформации образца без заметного возрастания напряжения. В этой зоне для малоуглеродистой стали наблюдается практически горизонтальный участок- площадка текучести, напряжение при которой называют пределом текучести sт. Для легированных сталей здесь имеется некоторый положительный наклон, т.е. нет ярко выраженной отмеченной площадки. В таких материалах за предел текучести принимается условная величина напряжения, при котором остаточная деформация составляет eр= 0,02...0,2 % (до 0,5%), и этот предел обозначается буквами s0,2.
Третья зона DG - зона упрочнения. Здесь удлинение возрастает, но увеличивается и напряжение. При этом происходит образование шейки, т.е. уменьшение площади сечения образца. В точке G напряжение в стержне становится максимальным. Напряжение при этом называется пределом прочности sв .
Если стержень, где напряжение меньше предела пропорциональности, т.е. s < sп , разгрузить до нуля, то длина восстановится, а s = 0.
Если же в стержне создать напряжение si, равное или выше предела текучести, то его длина увеличится, а после разгрузки сократится на некоторую величину. Часто считают, что при этом напряжение будет равным нулю, а остаточная деформация - eр (см. рис. 2.12) Однако на практике после холодной деформации в теле детали, изготовленной например из стали, возникают остаточные напряжения sо. Поэтому сокращение детали после разгрузки будет De= Е(si- so).
В случае скручивания, изгиба имеет место такая же закономерность. При этом для некоторых форм стальных деталей известна оценка величины остаточных напряжений: так при изгибе цилиндрического прутка so= 0,7sт; при изгибе прямоугольного стержня - so= 0,5sт [3].
При изучении пластической деформации различают основные напряжения, возникающие в упруго деформируемом теле, рабочие напряжения, фактически действующие в данный момент и распределяющиеся по телу в зависимости от его формы, внешних нагрузок, условий получения необратимых деформаций, а также дополнительные напряжения. Последние классифицируются как напряжения 1-го рода (взаимно уравновешивающиеся между большими объемами деформируемого тела), 2-го рода (взаимно уравновешивающиеся между отдельными зернами или группами зерен деформируемого тела), 3-го рода (взаимноуравновешивающиеся в пределах одного зерна). После прекращения действия внешней нагрузки снимаются только основные напряжения, а 99% остаточной энергии деформации составляют напряжения 3-го рода.
Если теперь деталь, ранее нагруженную свыше предела текучести, например, до точки F, опять нагрузить, то до значений напряжений, соответствующих точке F, пластических деформаций не будет. Материал приобретает способность передавать без пластических деформаций более высокие усилия. Это явление, повышение прочностных свойств в результате предварительного пластического деформирования называется нагартовкой или наклепом, который может быть снят термообработкой- отжигом.
Закон изменения напряжения от деформации при нагрузках, превышающих предел текучести, можно описать уравнением
si = s0,2+ Aenпл . (2-57)
Для некоторых материалов это уравнение имеет следующий вид :
сталь 10 si= 210+ 306e 0,21пл МПа;
сталь 20 si= 260+ 368e 0,18пл МПа;
сталь 40Х si= 570+ 422e 0,07пл МПа.
Иногда зону, характеризуемую выражением Z= Aenпл, описывают с помощью соотношения Z= П1De, где De - изменение относительного удлинения в зоне упрочнения, а модуль упрочнения определяется из таблицы 2.1.
Табл. 2.1
Данные по свойствам сталей
| Марка стали | Предел текучести, МПа | Модуль упрочнения П1, МПа |
| Ст. 10- ст.15, ст.1, ст 2. | ||
| Ст. 20- ст.25, ст.3, ст.4, 20К- 25К | ||
| Ст.30- ст.35, ст.5 | ||
| Ст.40- ст.45, ст.6, 15Х, 20Х | ||
| Ст.50- ст.60, ст.7, 20ХН, 30Х, 35Х | ||
| 40Х- 50Х, 40ХН- 50ХН |
Четвертую зону GS называют зоной местной текучести. Здесь удлинение образца происходит с образованием шейки и снижением общего напряжения в стержне, хотя напряжение в шейке возрастает. Затем происходит разрыв.
Стандартные испытания на сжатие обычно не проводят. Для большинства материалов при обычных расчетах модуль упругости, пределы упругости и текучести при сжатии и растяжении считаются одинаковыми.
В качестве показателей пластичности материала используют относительное остаточное удлинение образца после разрыва
d= (lp- l0)/ l0
и относительное остаточное уменьшение площади поперечного сечения в шейке после разрыва
y= (f0- fp)/ f0.
Уменьшение поперечного сечения при упругих деформациях характеризует также коэффициент Пуассона
c= Drl/(rDl).
(Обычно этот коэффициент обозначают буквой m, но так же обозначают и коэффициент трения и др. В связи с этим здесь для коэффициента Пуассона применена буква c.)
При нагреве механические характеристики металлов изменяются (см. рис. 2.13.).
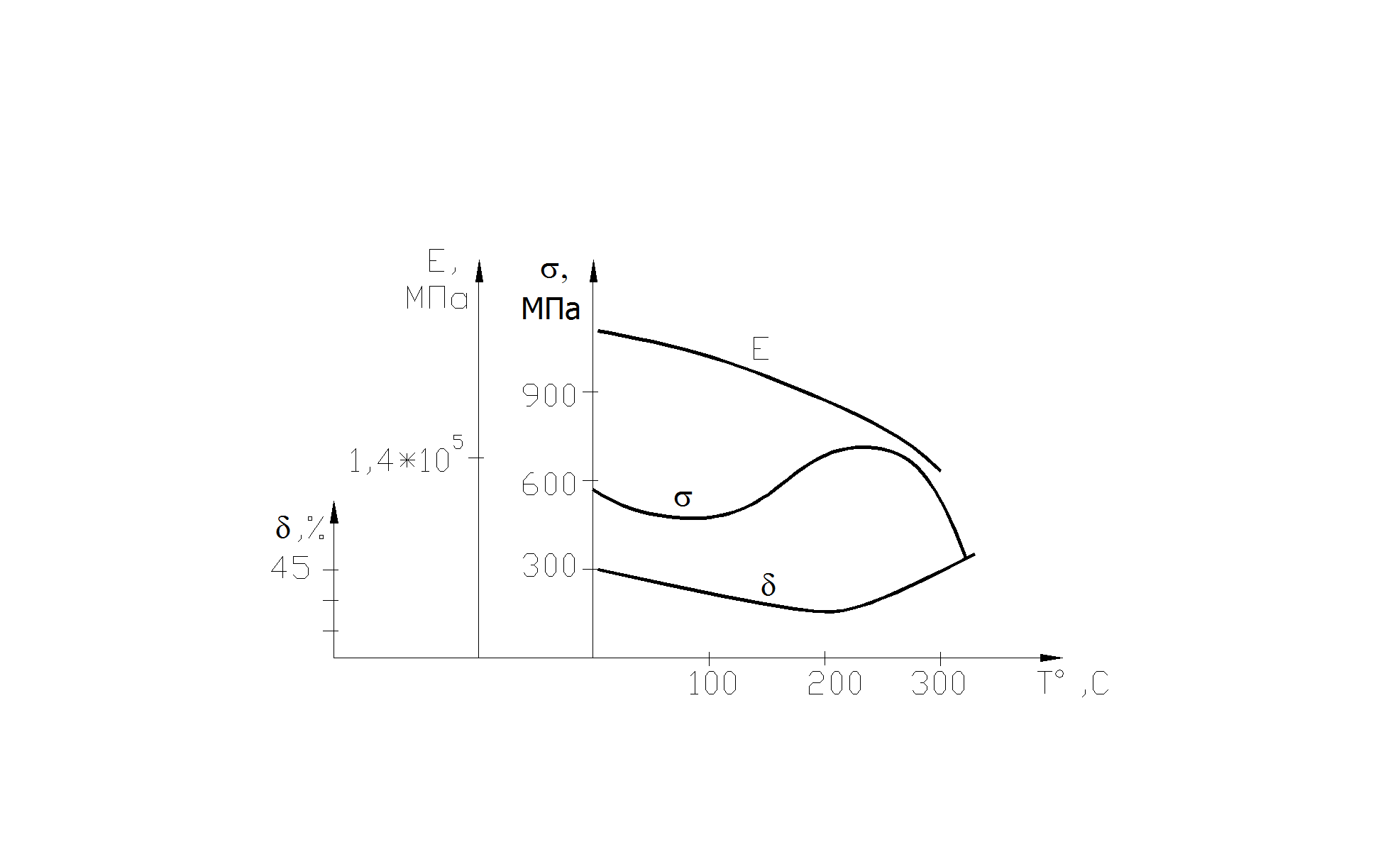
Рис.2.13
Влияние температуры на механические характеристики металлов.
Во время проектирования теплообменных апаратов необходимо также учитывать:
-предел длительной прочности- отношение силы, при которой происходит разрушение растянутого образца через заданный промежуток времени к первоначальной площади;
- предел ползучести- напряжение, при котором деформация за заданный промежуток времени достигает заданной величины.
Кроме выше указанных характеристик материалов есть и другие параметры, знание которых необходимо при разработке машин.
Дата добавления: 2015-02-23; просмотров: 916;
