Геометрические характеристики плоских сечений.
Из вышеизложенного следует, что нормальные и касательные напряжения, деформации зависят от геометрических характеристик сечений деформируемых деталей.
Площадь сечения.
Зависит от формы:
круг- s= p R2= pD2/4;
кольцо- s= p(R2- r2)= pD2(1- k2), k= d/D;
прямоугольник s= bh;
треугольник s= 0,5bh,
где D, R,d, r, h- соответственно, наружные диаметр и радиус, внутренние диаметр и радиус, сторона и высота.
Статические моменты сечения.
Статический момент относительно оси z
Sz=  ydA.
ydA.
Статический момент относительно оси y
Sy=  zdA.
zdA.
При параллельном переносе осей будет y1= y- b, а z1= z- a.
Тогда
Sz1=  y1 dA=
y1 dA=  ( y- b )dA= Sz- bA;
( y- b )dA= Sz- bA;
Sy1=  z1 dA=
z1 dA=  ( z- a )dA= Sy- aA. (2-113)
( z- a )dA= Sy- aA. (2-113)
Здесь А- площадь сечения.
Среди семейства параллельных осей z, y можно найти оси, относительно которых статический момент Sz1 или Sy1 будет равен нулю. Такую ось называют центральной, а точку их пересечения - центром тяжести сечения.
Если начало координат будет в точке C- центре тяжести, то ее координаты можно определить следующим образом
zC= a= A-1  z dA= Sy /A; yC= b= A-1
z dA= Sy /A; yC= b= A-1  y dA= Sz /A. (2-114)
y dA= Sz /A. (2-114)
Пример 2.3:
1.Прямоугольник. Найти на каком расстоянии от основания b находится центр тяжести.
dA= bdz
Sy=  z dA=
z dA= 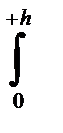 zbdz= bz2/2½
zbdz= bz2/2½ 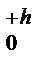 = bh2/2.
= bh2/2.
zC= Sy/A= (bh2/2)/(bh)= h/2.
Выполнив такие же операции относительно оси y, получим, что абсцисса центра тяжести равна
yC= b/2.
2. Треугольник неравнобочный (Рис. 2.23). Основание b лежит на оси ОХ1. На каком расстоянии от основания находится центр тяжести.
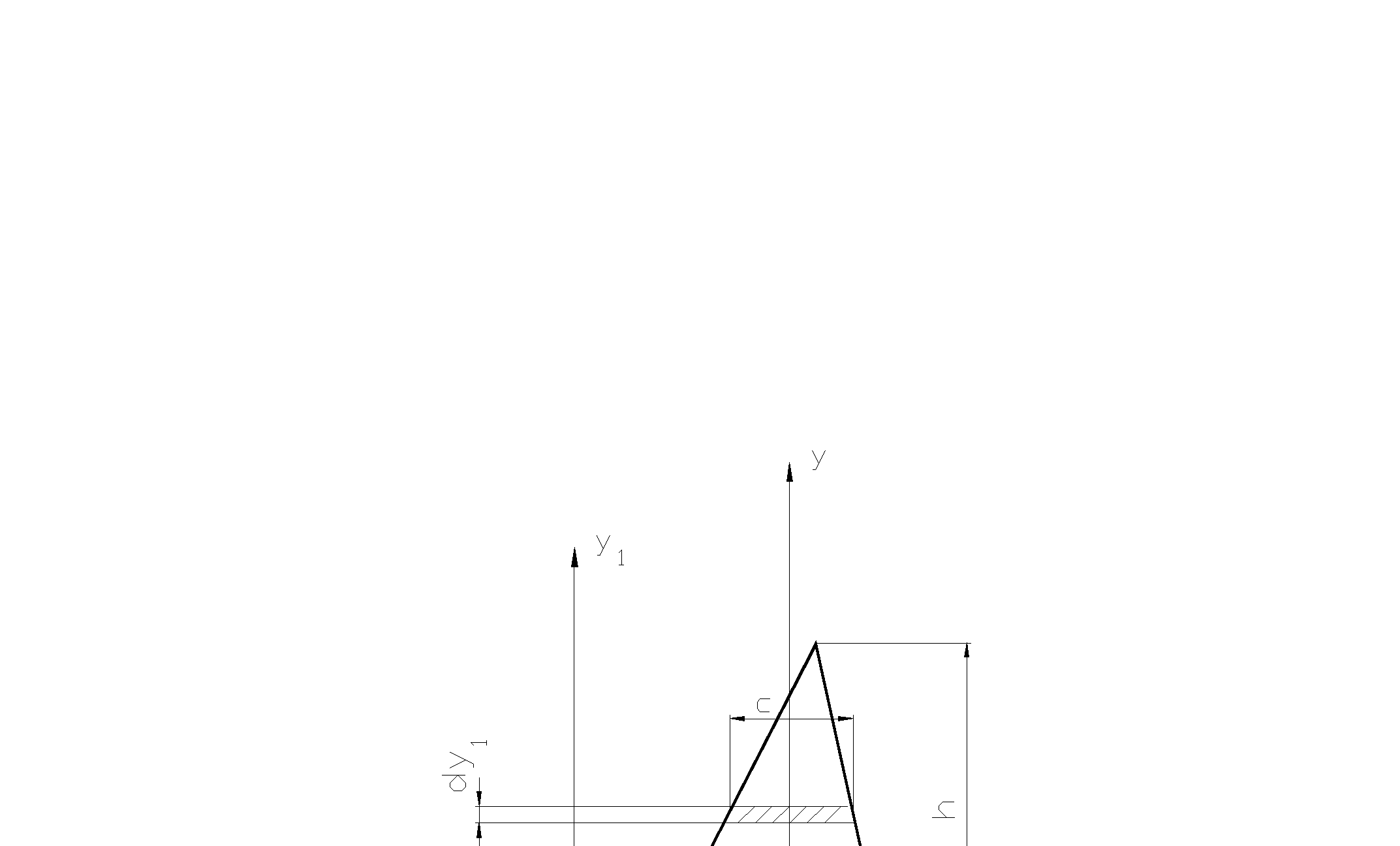
Рис.2.23.
Определение центра тяжести
треугольника.
Sх1=  y1 dA.
y1 dA.
dA= cdy1.
Из подобия треугольников находим c=b(h- y1)/h, где h - высота.
Таким образом,
Sx1=  y1 dA=
y1 dA=  y1[ b(h-y1)/h]dy1 = bh-1
y1[ b(h-y1)/h]dy1 = bh-1 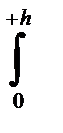 (h-y1)y1dy1= bh2/6. (2-115)
(h-y1)y1dy1= bh2/6. (2-115)
Отсюда
yС= Sx1/A= (bh2/6)/(bh/2)= h/3. (2-116)
Моменты инерции сечения.
Из предыдущего изложения следует, что существуют осевые, полярные моменты инерции. Кроме того, рассматриваются центробежные моменты инерции.
Осевой момент инерции относительно оси z
Jz=  y2 dA.
y2 dA.
Осевой момент инерции относительно оси y
Jy=  z2 dA.
z2 dA.
Полярный момент инерции относительно полюса O, размещенного в начале координат
Jр=  r2 dA=
r2 dA=  (z2+ y2) dA= Jy+ Jz. (2-117)
(z2+ y2) dA= Jy+ Jz. (2-117)
Центробежный момент инерции относительно осей z, y
Jzy= Jyz =  yz dA. (2-118)
yz dA. (2-118)
Центробежный момент инерции может иметь разные знаки (+), (-).
Значения моментов инерции зависят от положения сечения в осях координат.
Доказано, что при параллельном перемещении осей координат z1Oy1 в положение zOy моменты инерции сечений будут
Jz= Jz1+ 2aSz1+ a2A; Jy= Jy1+ 2bSy1+ b2A; Jzy= Jz1y1+ aSy1+ bSz1+ abA.
Если оси O1z1 и O1y1 являются центральными, то статические моменты равны нулю, последние соотношения примут вид
Jz= Jz1+ a2A; Jy= Jy1+ b2A; Jzy= Jz1y1+ abA. (2-119)
Для полярного момента инерции при параллельном переносе осей из центра тяжести в произвольную точку
Jp= Jz+ Jy= Jp1+ (a2+ b2)A. (2-120)
Момент инерции сложного сечения находят как сумму моментов инерции составных частей этого сечения.
В случае поворота сечения на угол a получим новые оси
u= z cosa + y sina; u= y cosa- z sina.
Тогда
Ju=  u2 dA.= Jzcos2a - Jzy sin (2a) + Jysin2a;
u2 dA.= Jzcos2a - Jzy sin (2a) + Jysin2a;
Ju=  u2 dA.= Jzsin2a + Jzy sin (2a) + Jycos2a;
u2 dA.= Jzsin2a + Jzy sin (2a) + Jycos2a;
Juu= Jzy cos(2a)+ 0,5(Jz- Jy)sin (2a). (2-121)
Из первых 2-х выражений следует Ju+ Ju= Jz+ Jy= const.
Из d Ju / da получим
d Ju / da= 2Jz cosa sina+ 2Jzycos(2a)- 2Jysina cosa =0
tg(2a)= 2Jzy/(Jy- Jz). (2-122)
Следовательно, если a= a0, т.е. при отсутствии поворота Jzy= 0.
Оси, относительно которых Jzy= 0, а осевые моменты имеют экстремальные значения, называют главными осями. Оси симметрии всегда главные. Если же главные оси проходят через центр тяжести, то их называют главными центральными осями, а соответствующие им осевые моменты инерции называются главными центральными моментами инерции.
Jmax/min= 0,5(Jy+ Jz) ± [0,25(Jy- Jz)2+ J2yz]1/2. (2-123)
Пример 2.4:
3. Определить относительно центральной оси Oz момент инерции прямоугольника высотой h, шириной основания b (рис.2.24,а) .
Jz=  y2 dA.= b
y2 dA.= b 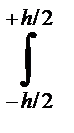 y2dy= bh3/12. (2-124)
y2dy= bh3/12. (2-124)
4. Определить момент инерции прямоугольника относительно оси О1z1, проходящей через основание (Здесь dA= bdy1).
Jz1= b 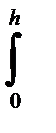 y21dy1 = bh3/3. (2-125)
y21dy1 = bh3/3. (2-125)
5. Определить центробежный момент инерции сечения прямоугольника относительно осей О1y1O1z1 (рис.2.24,а)
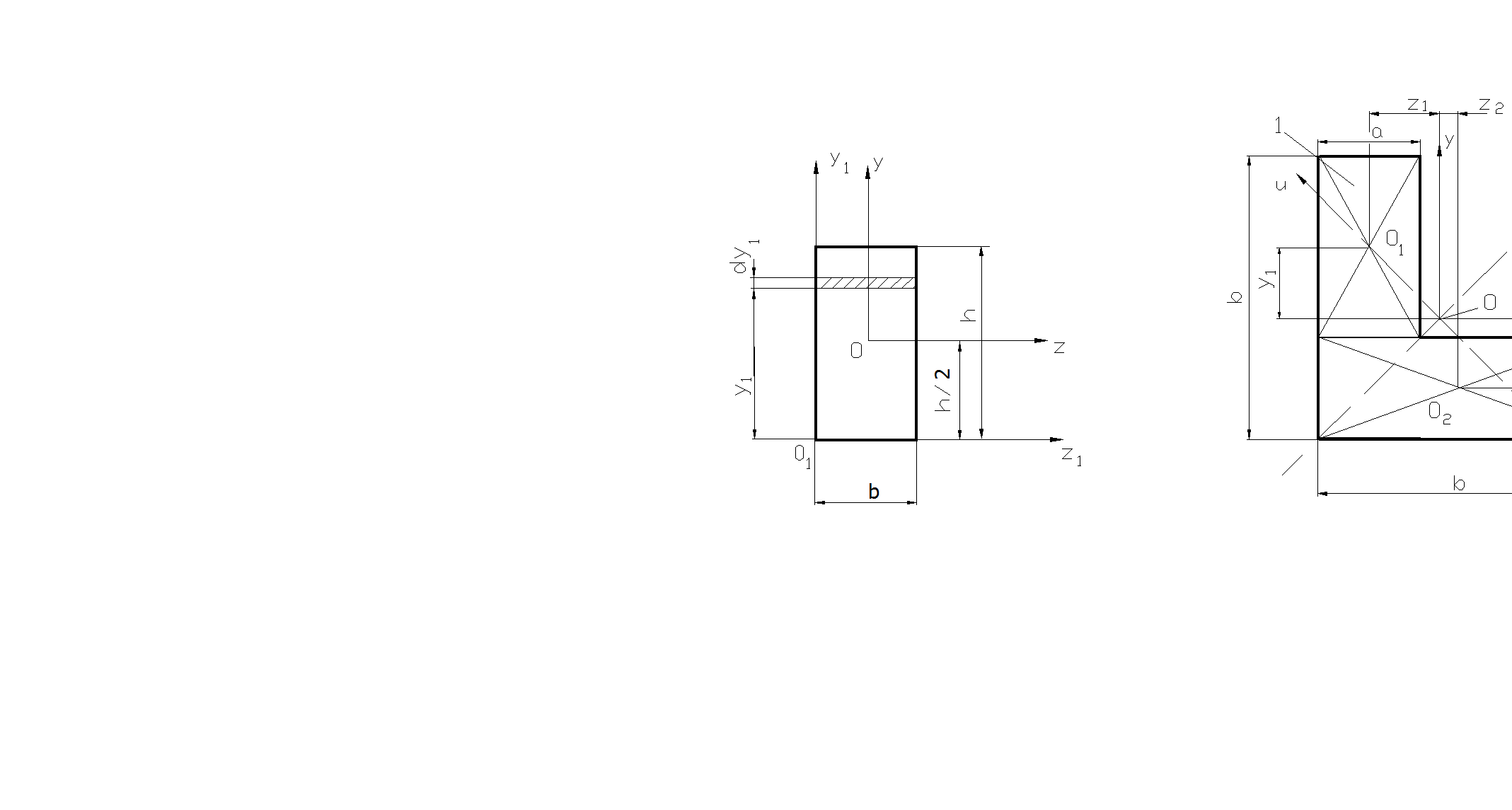
а) б)
Рис. 2.24 Определение моментов инерции сечений.
Здесь смещения относительно осей YOZ будут, соответственно, –b/2; -h/2. Тогда
Jy1z1= Jyz+ (b/2(h/2)bh= 0+ b2h2/4= b2h2/4. (2-126)
6. Определить момент инерции круга диаметром d относительно оси Оz
Сначала определим полярный момент инерции Здесь dA= 2prdr
Jp=  r2 dA= 2p
r2 dA= 2p 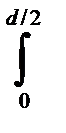 r3dr= pd4/32= pr4/2. (2-127)
r3dr= pd4/32= pr4/2. (2-127)
Так как Jp= Jz + Jy, то
Jy= pd4/64= pr4/4. (2-128)
7. Определить центральные и главные моменты инерции уголка равнобокого при a= 4 мм, b= 20 мм, расстояние от основания до центральной оси z составляет c= 6,4 мм (рис.2.24,б).
Так как уголок равнобокий, то Jz= Jy. Условно далее разделим сечение на 2 прямоугольника с центрами тяжести О1 и О2.
Центральные моменты инерции уголка
Jz= Jz(1)+ Jz(2); Jzy= Jzy(1)+ Jzy(2).
Учитывая Jz= Jy и выражение (2-122), получим, что tg(2a)= ¥.
Это означает, что угол наклона главных осей составляет a= 45°
При этом главные центральные моменты инерции составляют
Ju= Jzcos245°- Jzysin90°+ Jysin245°= Jz- Jzy.
Схема вычислений главных моментов инерции приведена в таблице 2.2.
При этом центробежные моменты инерции частей сечения относительно собственных центральных осей равны нулю.
По формуле (2-121) находим главные центральные моменты инерции (a0= 45°):
Ju= 5028,8- (-2844)=7872,8 мм4.
Ju= Jz+ Jzy= 5028+(-2844)=2184 мм4.
Таблица 2.2
| Номе-ра | Пло-ща-ди | Координаты центров тяжести | Моменты инерции площадей частей, мм4 | ||||
| час-тей | час-тей, | частей в осях коорди-нат yOz1, мм | Jzi= bih3i/12+ yi2A | Jziyi= ziyiAi | |||
| Мм2 | yCi | zCi | bh3/12 | y2iA | Jz | Jzy | |
| 5,6 | -4,4 | 4*163/12=1365,3 | 5,62*64= 2007 | 3372,3 | 64(-4,4)5,6=-=1577 | ||
| -4,4 | 3,6 | 20*43/12= 106,7 | 4,42*80= 1548,8 | 1656,5 | 80*3,6(-4,4)=-=1267 | ||
| å | - | - | - | - | 5028,8 | -2844 |
Дата добавления: 2015-02-23; просмотров: 1113;
