Вычислительная сложность метода Гаусса с полным выбором главного элемента
Процесс подсчета общего оличества операций для решения СЛАУ методом Гаусса с полным выбором главного элемента отличается от предыдущего пункта лишь способом выбора главного элемента. Именно: выбор главного элемента перед исключением в первом столбце матрицы СЛАУ осуществляется по всей матрице СЛАУ, а значит для такого выбора потребуется сравнить между собой 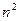 элементов, для чего потребуется провести
элементов, для чего потребуется провести 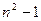 операцию сравнения. После выбора главного элемента и перестановки соответствующих строк и столбцов матрицы и соответствующих элементов вектора правой части (это подробно описано в лекции 8), осуществляется пересчет элементов матрицы и вектора правой части, который ничем не отличается от описанного в предыдущем пункте настоящей лекции. Перед проведением исключений во втором столбце матрицы СЛАУ (второй шаг метода Гаусса) выбор главного элемента осуществляется в области матрицы СЛАУ, расположенной ниже первой строки и правее первого столбца (см.лекц.8), содержащей
операцию сравнения. После выбора главного элемента и перестановки соответствующих строк и столбцов матрицы и соответствующих элементов вектора правой части (это подробно описано в лекции 8), осуществляется пересчет элементов матрицы и вектора правой части, который ничем не отличается от описанного в предыдущем пункте настоящей лекции. Перед проведением исключений во втором столбце матрицы СЛАУ (второй шаг метода Гаусса) выбор главного элемента осуществляется в области матрицы СЛАУ, расположенной ниже первой строки и правее первого столбца (см.лекц.8), содержащей 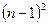 элементов, для чего потребуется провести
элементов, для чего потребуется провести 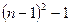 операцию сравнения. И т.д. Перед проведением исключений в
операцию сравнения. И т.д. Перед проведением исключений в 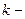 столбце матрицы СЛАУ для выбора главного элемента потребуется провести
столбце матрицы СЛАУ для выбора главного элемента потребуется провести 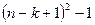 операций сравнения. Всего в процесс прямого хода метода Гаусса потребуется провести
операций сравнения. Всего в процесс прямого хода метода Гаусса потребуется провести
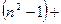
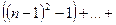
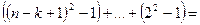
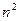 +
+ 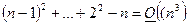
сравнений. Все же остальные операции (пересчет элементов при исключении) не отличаются от того, что было рассмотрено выше в методе Гаусса с частичным выбором главного элемента, и в совокупности оцениваются как 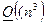 арифметических операций. Таким образом общее количество операций для проведения прямого хода метода Гаусса при полном выборе главного элемента составит:
арифметических операций. Таким образом общее количество операций для проведения прямого хода метода Гаусса при полном выборе главного элемента составит:
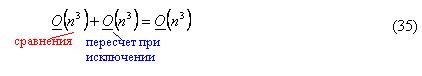
Вычислительная сложность обратного хода метода Гаусса здесь будет определяться также как, как при частичном выборе главного элемента и составит 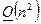 операций.
операций.
Таким образом, вычислительная сложность метода Гаусса с полным выбором главного элемента решения СЛАУ размером 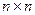 равна
равна 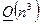 :
:
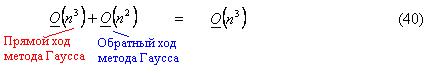
Дата добавления: 2015-03-20; просмотров: 2928;
