Зональная система плоских прямоугольных координат Гаусса

Для изображения на плоскости значительных частей земной поверхности применяют картографические проекции. Из множества проекций выбирают такую, которая для территории любой страны, имеет наименьшие значения искажений длин, углов и площадей. В нашей стране принята равноугольная поперечная цилиндрическая проекция Гаусса. Немецкий ученый геодезист и математик К.Ф.Гаусс предложил проектировать земную поверхность на плоскость не всю целиком, а по частям, ограниченным меридианами через 6° по долготе, которые он назвал зонами. Каждую зону проектируют на плоскость отдельно. На земном шаре 60 зон, счет их ведется от Гринвичского меридиана на восток. В каждой зоне средний меридиан зоны и экватор изображают прямыми линиями, а все остальные меридианы и параллели являются криволинейными. Средний меридиан зоны принимают за ось Х и поэтому называют осевым меридианом зоныс положительным направлением на север. За ось Y принимают перпендикулярное осевому меридиану зоны изображение экватора с положительным направлением на восток. Начало координат в пересечении осевого меридиана с экватором. Ординаты (расстояния от точки до оси Х) у’ точек, расположенных к востоку от осевого меридиана зоны - положительные, а к западу – отрицательные. Точки, расположенные в северном полушарии имеют положительные абсциссы, а в южном – отрицательные. Наша страна расположена в северном полушарии, поэтому абсциссы всех точек положительные. Чтобы избежать неудобства пользования отрицательными ординатами их искусственно делают положительными. Для этого ординату начала координат принимают не нуль, а 500км (500000м), т.е. координаты точки O имеют значения: Х_о = 0 ; Y_о = 500км. Можно считать, что начало ординат смещено на запад на 500км от осевого меридиана зоны. Такие ординаты называют преобразованными, обозначают у. Их вычисляют через непреобразованные ординаты - расстояние от точки до осевого меридиана зоны: у = у’ + 500км. Таким образом, ординаты точек, расположенных к западу от осевого меридиана зоны, имеют значения меньше 500км, а к востоку – больше 500км. Так как в каждой из 60 зон координаты одинаковые, то для однозначного определения положения точек на земном шаре надо знать номер зоны. Номер зоны указывают в значении ординат, его приписывают слева к значению километров ординаты. Таким образом, ордината имеет вид четырех или пятизначного числа (4690, 59300). В такой записи три последние цифры (в том числе и нули) собственно преобразованная ордината в км, а одна или две первые цифры - номер зоны. Например, запись ординаты у = 13692 обозначает, что точка находится в 13 зоне, ее преобразованная ордината равна 692км и что точка расположена на расстоянии 192км к востоку от осевого меридиана зоны (у’ = 692км – 500км = +192км). Если у = 4308, то точка расположена в 4 зоне и западнее осевого меридиана на 192км (у’ = 308км – 500км = - 192км). То есть, когда нужно определить непреобразованную ординату, то из преобразованной ординаты (без номера зоны) надо вычесть 500км (у’ = у - 500км). Для удобства пользования прямоугольными координатами на картах проводят линии параллельные координатным осям, их называют координатными линиями. Расстояние между ними соответствует 1км или 2км на местности. Они образуют сетку квадратов, называемую координатной или километровой сеткой. У пересечений линий сетки с рамкой листа карты, между внутренней и внешней рамками, подписывают значения прямоугольных координат линий сетки: абсциссы у западной и восточной сторон рамки, а ординаты (преобразованные) с номером зоны - у южной и северной сторон рамки. Для удобства пользования в значениях ординат десятки и единицы километров располагают справа от вертикальной линии сетки крупными цифрами, а сотни километров и номер зоны – слева от линии и цифрами меньших размеров. В значении абсциссы десятки и единицы километров подписывают также цифрами большего размера, чем тысячи и сотни. 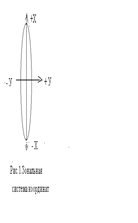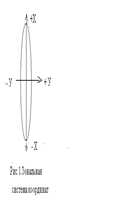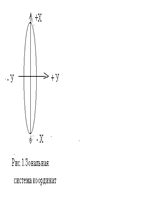При создании крупномасштабных планов масштаба 1:5000 и крупнее, применяют трехградусные зоны, осевыми меридианами которых являются осевые и граничные меридианы шестиградусных зон.