Прямая и обратная геодезические задачи
Из всего многообразия задач, решаемых в геодезии, выделяют две: прямую и обратную геодезические задачи. Прямая геодезическая задача заключается в определении координат (XВ;YВ) конечной точки отрезка АВ прямой линии по его длине (горизонтальному проложению d), направлению (дирекционному углу α или румбу r) и координатам (XА;YА) начальной точки.
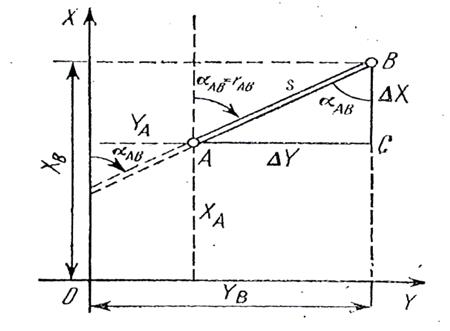
Рис.1.12. Прямая и обратная геодезические задачи
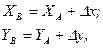 (14)
(14)
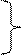 |
где 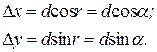 (15)
(15)
Формулы (15) справедливы при любых значениях α..
При проектировании конечных точек отрезка на координатные оси образуется прямоугольный треугольник (Рис.1.12), в котором гипотенузой является длина отрезка, а катетами – приращения координат. Продлим отрезок до пересечения его с осью Х. Угол в точке пересечения положительного направления оси Х с линией есть дирекционный угол линии. Поскольку синусы (sin) и косинусы (cos) углов, различающихся на 180,° одинаковые то для вычисления приращений координат используют острые углы – румбы, определяя знаки приращений по четверти, в которой расположен отрезок. Решая таким путем многократно прямую геодезическую задачу можно вычислить координаты всех точек поворота ломаной линии, если известны координаты начальной точки, длины отрезков и их дирекционные углы.
Обратная геодезическая задача заключается в нахождении длины (горизонтального проложения ) и направления (румба и дирекционного угла) отрезка прямой линии по координатам его конечных точек. Возможны два пути решения: 1) Сначала определяют направление (дирекционный угол), затем длину отрезка; 2) Сначала определяют длину отрезка, а затем его направление. Основным считается первый путь, второй используется для контроля.
Первый путь решения.
1.Заданы прямоугольные координаты Х и У конечных точек отрезка, его длина d и
дирекционный угол a.
2.Вычисляют приращения координат D X и DY , вычитая из значений координат конечной точки отрезка координаты его начальной точки. 3.Вычисляют румб по формуле r = arctg DY/ D X = arctg (Y2 – Y1)/ (X2—X1). 4.Вычисляют дирекционный угол по формуле зависимости между румбом и дирекционным углом, предварительно определив по знакам приращений координат номер четверти, в которой расположен отрезок (рис. 1.11 и табл.
5.Вычисляют длину отрезка по формулам:d = DX/ cosa= DY/ sina=Ö DX² + DY² .
Второй путь решения.
1. Определяют длину отрезка по теореме Пифагора d = ÖDX2+ DY2
2.Вычисляют румб (два значения): r = arccos DX / d ; r = arcsin DY/ d .
3.Вычисляют дирекционный угол по формулам зависимости между румбами и
дирекционными углами, если расхождение двух значений румба не превышает точности вычислений.
Результаты вычислений помещают в табл.
Второй вариант используется для контроля.
Дата добавления: 2015-03-19; просмотров: 3319;
