А в проекциях на оси цилиндрической системы координат rΘz при осевой симметрии будет
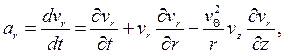
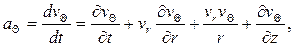(1.6*)
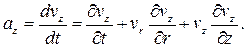
При изучении движения сплошной среды широко используют понятие поля скалярной и векторной величин. Совокупность значений той или иной величины, заданной в каждой точке рассматриваемой области, называется ее полем.
Если рассматриваемая величина — скаляр (давление р, плотность ρ, температура T и т.д.), то поле называется скалярным; если же — вектор (перемещение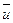 
, скорость 
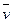, ускорение 
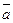и т. д.), то поле называется векторным.
Как скалярная, так и векторная величины не зависят от выбранной системы координат. Так как вектор определяется тремя числами (компонентами или проекциями на оси координат), то векторное поле равнозначно трем скалярным полям. Однако эти поля уже зависят от системы координат.
На примере поля плотности ρ и поля скоростей 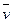рассмотрим некоторые общие характеристики полей.
Поле ρ = ρ(х1; х2, х3), характеризующее данный процесс или движение, может быть стационарным dρ/dt=0 (установившимся) или нестационарным dρ/dt≠0 (неустановившимся). Одно и то же движение может быть как установившимся, так и неустановившимся, все зависит от выбора системы координат, относительно которой изучается движение. Поэтому говорят, что установившееся (стационарное) движение — понятие относительное.
Для любого векторного поля используют понятие векторных линий. Векторные линии— это семейство линий, касательные к которым совпадают с направлением вектора.
В случае поля скоростей эти линии называются линиями тока.
Если выбрать произвольную кривую С, не совпадающую с линией тока, и через каждую ее точку провести линию тока, то образуется поверхность тока. Если кривая С замкнута, поверхность тока называется трубкой тока.
Аналитически семейство линий тока можно найтииз условия коллинеарности элемента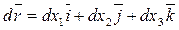 
, взятого вдоль линии тока, и вектора скорости 
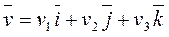,т.е.
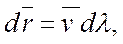
или в проекциях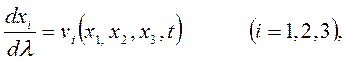 
(1.7)
где dλ— скалярный параметр. Это и есть дифференциальные уравнения линий тока. Они отличаются от уравнений, описывающих закон движения или траектории движения частиц сплошной среды
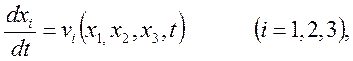(1.8)
тем, что в уравнениях (1.7) t — параметр, а в уравнениях (1.8) t — переменная величина.
Таким образом, линии тока не совпадают с траекториями. Они совпадают только при движениях установившихся (так как в этом случае между уравнениями (1.7) и (1.8) нет различия) и при неустановившихся, когда поле скоростей изменяется по величине, но не изменяется по направлению.
Если задана плотность (или любая другая скалярная величина, например Т- температура) как функция переменных Эйлера, то в каждый момент времени можно рассматривать поверхность
T(x1,x2,x3,t)=const, (1.9)
 |
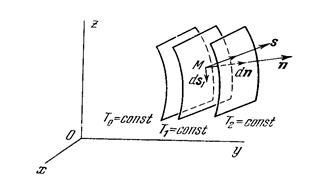которая называется поверхностью равного уровня или эквипотенциальной.
Рис. 2 Поверхности равного уровня.
Вектор, направленный по нормали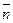 
в какой-либо точке М поверхности (1.9) в сторону роста T и равный по величине 
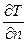, называется вектором-градиентомскалярной функции Tв точке М.
Он обозначается и вычисляется так:
,
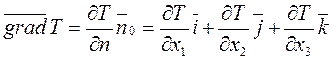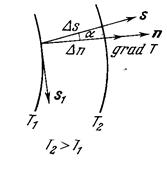
Рис.3 Вектор – градиент температуры
где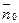 
и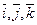 
— единичные векторы по направлению 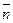и вдоль координатных осей.
Проекция вектора grad T на некоторое направление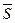 
определяет изменение температуры в этом направлении:
,
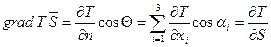где Θ — угол между направлениям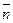и и 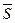; cosαi — направляющие косинусы вектора .
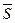Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (1.9).
Если в поле скорости 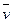(или любой другой векторной величины) мысленно провести некоторую поверхность S и в каждой ее точке задать нормаль 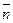, то для определения объема жидкости, протекающей за единицу времени сквозь поверхность S, необходимо вычислить интеграл
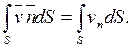
Этот интеграл называется потоком скоростичерез поверхность S.
Поток скорости сквозь замкнутую поверхность S, отнесенный к единице объема V, заключенного внутри S, называется расхождениемили дивергенциейскорости, т. е.
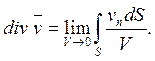
Дата добавления: 2015-03-07; просмотров: 2505;