В цилиндрической системе координат (r, Θ, z) при осевой симметрии
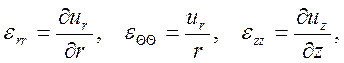
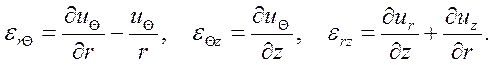(1.18)
Компоненты вектора перемещений ur, uΘ, uz связаны с компонентами
ui (i=1, 2, 3) обычными соотношениями преобразования координат при повороте системы вокруг оси oz:
ur= u1cos Θ + u2sin Θ,
uΘ= - u1 sin Θ + u2cos Θ,
uz= u3.
Если иметь в виду связь между координатами x1= r cos Θ, x2 = r sin Θ и x3 = z, то доказать справедливость перехода от формул (1.17) к формулам (1.18), или наоборот, не представляет труда.
Так как деформация отрезка не зависит от выбора направлений координатных осей, то правая часть в формуле (1.16) инвариантна преобразованию системы координат, т. е.
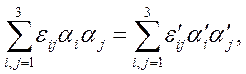(1.19)
где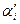 
и 
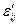— направляющие косинусы и компоненты деформаций в новой 
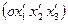системе координат. Для вычисления 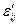через εij, достаточно в равенстве (1.19) выразить 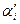через αi и сравнить коэффициенты при одинаковых αi, αj.
В любой точке тела всегда существует по крайней мере одна тройка взаимно перпендикулярных направлений, таких, что деформация элемента в окрестности точки определяется только удлинением (укорочением) εii = εi вдоль этих направлений без изменения прямых углов (εij = 0, i≠j). Такие направления называются главными осями деформаций, а величины εi (i = 1, 2, 3) — главными удлинениями, которые могут быть найдены из следующего кубического уравнения:
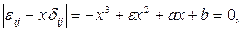
где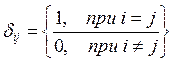 
— символ Кронекера.
Ясно, что коэффициенты этого уравнения не зависят от выбора системы координат, т. е. они инвариантны. Первый коэффициент ε этого уравнения
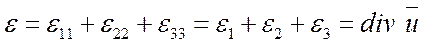(1.20)
и имеет простой геометрический смысл — относительное изменение объема в окрестности точки. Коэффициенты а и b геометрического смысла не имеют и поэтому не являются характеристикой деформаций.
Характеристикой искажения формы элемента сплошной среды служит инвариантная величина
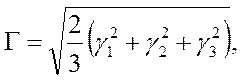
Дата добавления: 2015-03-07; просмотров: 1258;