Для характеристики деформационного состояния служит параметр Надаи

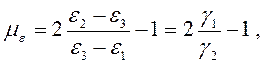(1.22)

который изменяется в пределах от -1 (при чистом удлинении) до +1 (при частичном укорочении). В случае чистого сдвига μ_ε = 0. При всестороннем расширении (или сжатии) μ_εсмысла не имеет.

Часто удобно пользоваться следующим представлением компонент деформаций:

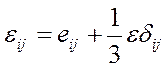, (1.23)

где e_ij — компоненты, характеризующие только деформации сдвига, называемые компонентами девиатора деформаций,

δ_ij—символ Кронекера.
Отсюда следует, что компоненты тензора деформации растяжения (сжатия) ε_ii отличаются от соответствующих компонент девиатора е_ii на 1/3 объемной деформации, а компоненты деформации сдвига не отличаются, т. е.

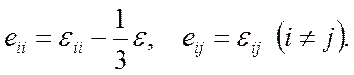
Если известны компоненты деформации ε_ij как функции декартовых координат х_i, то для однозначного определения 3-х компонент u_i вектора перемещений из 6-ти соотношений (1.17) необходимо и достаточно, чтобы функции ε_ij удовлетворяли условиям совместимости (или неразрывности) деформаций Сен-Венана:

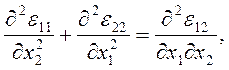
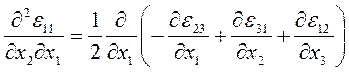(1.24)

и т. д., всего 6 условий (остальные получаются из выписанных круговой заменой индексов 1→2→3→1).