Напряжение зависит от положения элемента dS, т. е. от ориентировки его
в теле. Если требуется указать, что напряжение 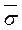 относится к площадке с нормалью п, то пишут
относится к площадке с нормалью п, то пишут  .
.
Проекции этого вектора на оси произвольной системы координат Ох1х2х3 обозначаются через σnj (j=1, 2, 3). В частности, проекции напряжений 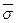 xi, отнесенные к площадкам, перпендикулярным к координатным осям Oxi, обозначаются через σij (i,j = 1,2,3), где σii называются нормальными напряжениями,
xi, отнесенные к площадкам, перпендикулярным к координатным осям Oxi, обозначаются через σij (i,j = 1,2,3), где σii называются нормальными напряжениями,
а σij = σji (i≠j) — касательными напряжениями, действующими на этих площадках (рис. 5). Легко доказать следующие очень важные соотношения:
σnj = 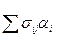 ( i, j = 1,2,3), (1.29)
( i, j = 1,2,3), (1.29)
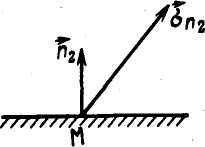
которые позволяют найти компоненты вектора напряжения для произвольной площадки с нормалью 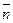 , проходящей через точку М; αi = cos(n, хi) (i = 1, 2, 3).
, проходящей через точку М; αi = cos(n, хi) (i = 1, 2, 3).
Поэтому говорят, что совокупность шести величин σij, называемых компонентами симметричного тензора напряжений, полностью характеризует напряженное состояние в точке тела М.
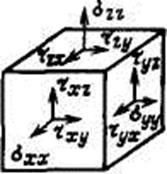
| Рис. 5. Расположение компонент тензора напряжений относительно выбранной декартовой системы координат |
| Рис. 6. Векторы напряжений в точке М, действующие в двух произвольно ориентированных площадках |
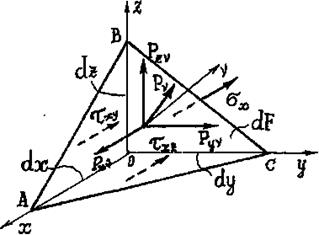
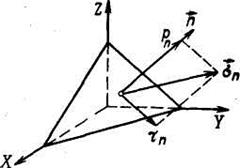
Рис. 7. Нормальная и касательная проекции вектора напряжения 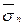
Пусть заданы две площадки, проходящие через одну и ту же точку М (рис. 6). Используя формулу (1.29), нетрудно доказать, что проекция напряжения 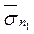 , действующего на первую площадку, на нормаль
, действующего на первую площадку, на нормаль 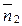 ко второй равна проекции напряжения
ко второй равна проекции напряжения 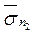 , действующего на вторую площадку, на нормаль
, действующего на вторую площадку, на нормаль 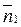 к первой и вычисляется по формуле
к первой и вычисляется по формуле
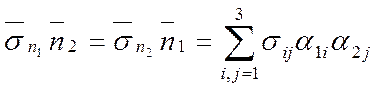
 (1.30)
(1.30)
где α1i и α2j — направляющие косинусы нормалей 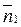 и
и 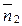 .
.
Эта формула позволяет вычислить проекцию на любое направление вектора напряжения, действующего на данную площадку.В частности, проектируя вектор 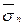 на направление нормали, получаем нормальное напряжение (рис. 7)
на направление нормали, получаем нормальное напряжение (рис. 7)
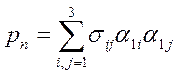 (1.31)
(1.31)
Касательное напряжение на этой же площадке равно
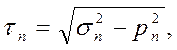 (1.32)
(1.32)
где σn — величина вектора напряжения 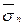 .
.
Из формулы (1.30) следуют формулы перехода от одной системы Ох1х2х3 координат к другой О 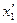
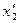
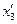 ;
;
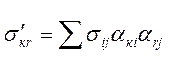 (1.33)
(1.33)
где σ'кr — компоненты тензора напряжений относительно новой системы координат;
αкi = cos( 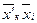 ), αrj = cos(
), αrj = cos( 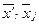 ).
).
Например, зависимость между напряжениями в декартовой (Ох1х2х3) и цилиндрической (r, θ, z) системах координат с общей осью Ox3 = Oz имеет вид
σrr = σ11cos2θ + σ22 sin2θ + σ12 sin 2θ;
σθθ= σ11 sin2θ + σ22 cos2θ - σ12 sin 2θ;
σzz = σ33; (1.34)
σrθ = 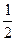 ( σ22 - σ11)sin 2θ + σ12 cos2θ;
( σ22 - σ11)sin 2θ + σ12 cos2θ;
σrz = σ13 cosθ + σ23sin θ;
σθz= - σ13 sinθ + σ23 cosθ;
где σrr—радиальное напряжение, действующее на площадке, перпендикулярной к радиусу; σθθ — тангенциальное (окружное) напряжение, действующее на площадке, нормаль которой перпендикулярна к радиусу.
Принимая во внимание известные соотношения аналитической геометрии
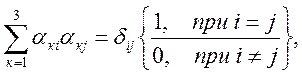
из формул (1.33) после суммирования левой и правой частей по к (при r = к) получается важное соотношение
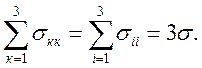 (1.35)
(1.35)
Оно показывает, что величина σ, называемая средним нормальным напряжением, инвариантна по отношению к преобразованию системы координат.
Характерной особенностью напряженного состояния сплошной среды является наличие в каждой точке тела, по крайней мере, трех взаимно перпендикулярных площадок, на которых касательные напряжения σij (i≠j) равны нулю. Направления нормалей к этим площадкам образуют главные направления, которые не зависят от исходной системы координат. Соответствующие напряжения σii=σi называются главными нормальными напряжениями.Поэтому любое напряженное состояние в рассматриваемой точке может быть вызвано растяжением (сжатием) окрестности точки в трех взаимно перпендикулярных направлениях.
Главные нормальные напряжения могут быть найдены из следующего кубического уравнения:
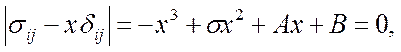
корни этого уравнения могут быть только вещественными.
Так как решения этого уравнения хi = σi (i=1,2,3) не зависят от выбора системы координат, коэффициенты σ, А, В также не должны зависеть, т. е. они инвариантны. Это еще одно доказательство инвариантности среднего напряжения
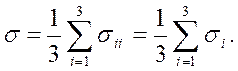 (1.36)
(1.36)
Два других инварианта физического смысла не имеют.
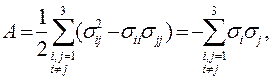
 |
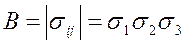 (1.37)
(1.37)
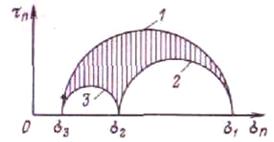
Рис. 8. Диаграмма Мора:
/, 2, 3 — окружности, координаты которых определяют нормальные и касательные напряжения на площадках, проходящих через главные оси 1, 2, 3 соответственно
Если главные направления совпадают с координатными осями (Охi), то формулы (1.31) — (1.34) упрощаются. Например, формулы (1.31) и (1.32) принимают вид
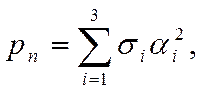 (1.38)
(1.38)
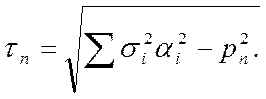
где αi= cos (n, xi).
Отсюда нетрудно получить, что напряжения рп и τn могут лежать только внутри области, заштрихованной на рис.8. Это так называемая диаграмма Мора, дающая наглядное представление о напряжениях в различных сечениях, проходящих через данную точку. Здесь принята нумерация главных осей такой, чтобы выполнялись условия
σ1 ≥ σ2 ≥ σ3 (1.39)
Практический интерес представляют сечения, проходящие через главные оси. На рис. 8 точкам какой-либо окружности 1, 2 или 3 отвечают площадки, содержащие соответствующую главную ось.
Дата добавления: 2015-03-07; просмотров: 1338;
