Таким образом, условия совместимости (1.24) являются уравнениями, которые связывают компоненты εij тензора деформаций.
Для анализа больших деформаций, если главные оси при деформации не поворачиваются, используются так называемые натуральные удлинения (укорочения)
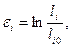
где li0, li —начальные и текущие длины элемента в соответствующих направлениях.
Характерные соотношения для малых деформаций являются справедливыми и для натуральных удлинений.
+++++++++++++++++++++++++++++++++++++++++++++++
О СКОРОСТЯХ ДЕФОРМАЦИЙ
Если скорость частиц сплошной среды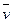 
= (v 1, v2, v3), то за бесконечно малый промежуток времени dt среда испытывает бесконечно малую деформацию, определяемую перемещениями ui = vidt(i = 1, 2, 3). Компоненты этих деформаций, вычисленные по формулам (1.17), имеют общий множитель dt, разделив на который, получим
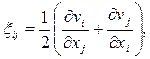(1.25)
где ξij —компоненты тензора скоростей деформаций.
Величины ξii определяют скорости удлинения (укорочения) единичных отрезков в направлениях охi, ξij(i≠j)— угловые скорости изменения первоначально прямых углов, составленных единичными отрезками вдоль координатных осей.
Подобно формуле (1.16) скорость удлинения (укорочения) любого единичного отрезка вычисляется по формуле
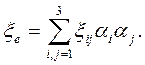
Аналогично соотношениям (1.20) — (1.22) инвариантами скорости деформации являются:
а) скорость относительного объемного расширения (сжатия)
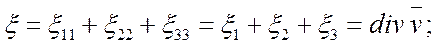(1.26)
б) интенсивность скоростей деформации сдвига относительно главных осей
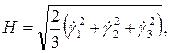(1.27)
где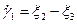 
, 
, 
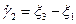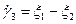— главные скорости сдвигов (относительно произвольной системы координат Н выражается формулой (1.21));
в) параметр Надаи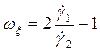 
.
Компоненты скорости деформации ξij, как и компоненты деформации εij, не могут быть произвольными. Они должны удовлетворять условиям совместимости, аналогичным условиям (1.24).
Подобно представлению (1.23) для компонент тензора {ξij} скоростей деформаций верно соотношение
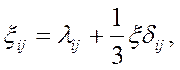(1.28)
Дата добавления: 2015-03-07; просмотров: 1158;